xy平面上の内分点・外分点｜座標を求める基本公式

中学数学から$xy$平面上に

$y=2x+1$は直線
$y=x^2$は放物線

といったように，様々なグラフを描いてきました．

このように$y=2x+1$や$y=x^2$といった$x, y$の等式があると，それに対応して座標上に図形が描かれます．

この図形と方程式の関係を考える上で，最も基本的な概念のひとつに内分と外分があります．

この記事では

数直線上の内分と外分の定義
数直線上の内分と外分の公式
平面上・空間上の内分と外分

について順に説明します．

「図形と方程式」の一連の記事

数直線上の内分と外分
1. 内分の定義
2. 外分の定義
数直線上の内分点，外分点の座標
1. 内分点
2. 外分点
平面上・空間上の内分と外分

数直線上の内分と外分

まずは線分の内分と外分の定義から説明します．

内分の定義

名前の通り線分の内側にある点のことで，次のように定義されます．

正の数$m$, $n$と線分$\mrm{AB}$を考える．線分$\mrm{AB}$上の点$\mrm{P}$が

$\begin{align*}\mrm{AP:BP}=m:n\end{align*}$

を満たすとき，点$\mrm{P}$は線分$\mrm{AB}$を$m:n$に内分するといい，点$\mrm{P}$をこの内部における内分点という．

内分の定義は分かりやすいですね．

とくに線分の中点は「$1:1$に内分する点」ということができますね．

外分の定義

名前の通り線分の外側にある点のことで，次のように定義されます．

異なる正の数$m$, $n$と線分$\mrm{AB}$を考える．線分$\mrm{AB}$の延長上の点$\mrm{Q}$が

$\begin{align*}\mrm{AQ:BQ}=m:n\end{align*}$

を満たすとき，点$\mrm{Q}$は線分$\mrm{AB}$を$m:n$に外分するといい，点$\mrm{Q}$をこの外分における外分点という．

この外分の定義において，$n<m$の場合と$m<n$の場合で，外分点が線分のどちらの延長上に存在するかが変わることに注意しましょう．

$n<m$のときは$\mrm{AQ}:\mrm{BQ}=m:n$から$\mrm{AQ}>\mrm{BQ}$なので，外分点$\mrm{Q}$は$\mrm{B}$側の延長上に存在します．

一方，$n>m$のときは$\mrm{AQ}:\mrm{BQ}=m:n$から$\mrm{AQ}<\mrm{BQ}$なので，外分点$\mrm{Q}$は$\mrm{B}$側の延長上に存在しますね．

このように外分の図を考える際はどちらの比の方が大きいかに注意してください．

数直線上の内分点，外分点の座標

数直線上の２点$\mrm{A}$, $\mrm{B}$の座標がそれぞれ$a$, $b$であるとしましょう．

このとき，線分$\mrm{AB}$の内分点の比・外分点の比から，内分点・外分点の値の座標を計算することができます．

以下では，数直線上の点$\mrm{X}$の値が$x$であることを$\mrm{X}(x)$と表しましょう．

これは平面上の座標を$\mrm{X}(x,y)$と表すのと同じ感覚です．

内分点

数直線上の２点$\mrm{A}(a)$, $\mrm{B}(b)$に対し，線分$\mrm{AB}$を$m:n$に内分する点を$\mrm{P}$の座標は

$\begin{align*}\mrm{P}\bra{\frac{na+mb}{m+n}}\end{align*}$

である．

$a<b$のときも$a>b$のときも同様に示されるので，$a<b$のときのみ示す．点$\mrm{P}$の座標を$p$とする．

このとき$a<p<b$なので，$\mrm{AP}=p-a$, $\mrm{PB}=b-p$だから，

$\begin{align*} &\mrm{AP}:\mrm{PB}=m:n \\\iff&(p-a):(b-p)=m:n \\\iff& m(b-p)=n(p-a) \\\iff& p=\frac{na+mb}{m+n} \end{align*}$

を得る．

例１

数直線上の点$\mrm{A}(2)$, $\mrm{B}(7)$に対して，線分$\mrm{AB}$を$2:3$に内分する点を$\mrm{P}(p)$としましょう．

このとき，内分の公式より

$\begin{align*}p=\frac{3\cdot2+2\cdot7}{2+3}=4\end{align*}$

となって，$\mrm{P}$の座標は$4$と分かりますね．

例２

数直線上の点$\mrm{A}(-1)$, $\mrm{B}(4)$に対して，線分$\mrm{AB}$の中点を$\mrm{P}(p)$としましょう．

このとき，点$\mrm{P}$は線分$\mrm{AB}$を$1:1$に内分するから，内分の公式より

$\begin{align*}p=\frac{1\cdot4+1\cdot(-1)}{1+1}=\frac{3}{2}\end{align*}$

となって，$\mrm{P}$の座標は$\dfrac{3}{2}$と分かりますね．

一般に数直線上の中点の座標は次で求められますね．

数直線上の２点$\mrm{A}(a)$, $\mrm{B}(b)$に対し，線分$\mrm{AB}$の中点$\mrm{M}$の座標は

$\begin{align*}\mrm{M}\bra{\frac{a+b}{2}}\end{align*}$

である．

この中点の公式はよく用いるので，当たり前にしておきましょう．

中点はよく$\mrm{M}$で表されますが，これは中点を意味する英単語“midpoint”の頭文字に由来しています．

外分点

数直線上の２点$\mrm{A}(a)$, $\mrm{B}(b)$に対し，線分$\mrm{AB}$を$m:n$に外分する点を$\mrm{Q}$の座標は

$\begin{align*}\mrm{Q}\bra{\frac{-na+mb}{m-n}}\end{align*}$

である．

数直線上の２点$\mrm{A}(a)$, $\mrm{B}(b)$に対し，線分ABを$m:n$に外分する点$\mrm{Q}(q)$の座標を求めます．

$n<m$のときも$n>m$のときも同様に示され，さらに$a<b$のときも$a>b$のときも同様に示されるので，$a<b$かつ$n<m$のときを示す．点$\mrm{Q}$の座標を$q$とする．

このとき$a<b<q$なので，$\mrm{AQ}=q-a$, $\mrm{QB}=q-b$だから，

$\begin{align*}\mrm{AQ}:\mrm{QB}=m:n&\iff(q-a):(q-b)=m:n \\&\iff m(q-b)=n(q-a) \\&\iff q=\frac{-na+mb}{m-n}\end{align*}$

を得る．

$\dfrac{-na+mb}{m-n}$の分母・分子に$-1$をかけると，

$\begin{align*}\frac{-na+mb}{m-n}=\frac{na-mb}{-m+n}\end{align*}$

となり両者はいつでも等しいので，外分点の座標は$\dfrac{na-mb}{-m+n}$と書いても同じことですね．

例３

数直線上の点$\mrm{A}(3)$, $\mrm{B}(7)$に対して，線分$\mrm{AB}$を$1:3$に外分する点を$\mrm{Q}(q)$としましょう．

このとき，外分の公式より

$\begin{align*}q=\frac{(-3)\cdot3+1\cdot7}{1-3}=1\end{align*}$

となって，$\mrm{Q}$の座標は$1$と分かりますね．

例４

数直線上の点$\mrm{A}(1)$, $\mrm{B}(4)$に対して，線分$\mrm{AB}$を$5:2$に外分する点を$\mrm{Q}(q)$としましょう．

このとき，外分の公式より

$\begin{align*}q=\frac{(-2)\cdot1+5\cdot4}{5-2}=6\end{align*}$

となって，$\mrm{Q}$の座標は$6$と分かりますね．

平面上・空間上の内分と外分

さて，$xy$平面上でも$xyz$空間の線分$\mrm{AB}$についても，同様に公式が得られます．

例えば，平面の場合は次の通りです．

$xy$平面上の２点$\mrm{A}(a_1,a_2)$, $\mrm{B}(b_1,b_2)$に対し，線分$\mrm{AB}$を$m:n$に内分する点を$\mrm{P}$，$m:n$に外分する点を$\mrm{Q}$とすると，それぞれの座標は

$\begin{align*}&\mrm{P}\bra{\dfrac{na_1+mb_1}{m+n},\dfrac{na_2+mb_2}{m+n}}, \\&\mrm{Q}\bra{\dfrac{-na_1+mb_1}{m-n},\dfrac{-na_2+mb_2}{m-n}}\end{align*}$

である．

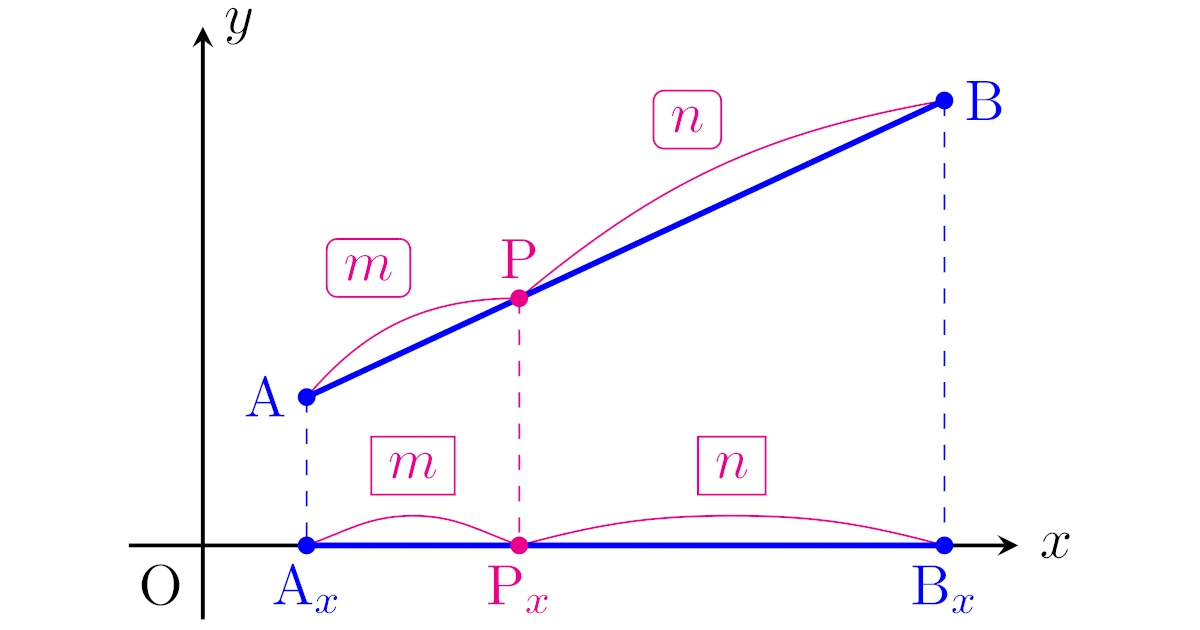
点$\mrm{A}$, $\mrm{B}$, $\mrm{P}$から$x$軸に下ろした垂線の足をそれぞれ$\mrm{A}_x$, $\mrm{B}_x$, $\mrm{P}_x$とする．

このとき，相似を考えると$\mrm{AP}:\mrm{PB}=m:n$より$\mrm{A}_x\mrm{P}_x:\mrm{P}_x\mrm{B}_x=m:n$が成り立つ．

すなわち，$\mrm{P}_x$は線分$\mrm{A}_x\mrm{B}_x$を$m:n$に内分するので，数直線に関する内分の公式より，点$\mrm{P}$の$x$座標は

$\begin{align*}\frac{na_1+mb_1}{m+n}\end{align*}$

である．

$y$軸に垂線を下ろすことにより$y$座標についても同様に成り立つ．外分についても同様に成り立つ．

$xyz$空間上の内分，外分についても，各軸に垂線を下ろすことにより以下の公式が得られます．

空間上の２点$\mrm{A}(a_1,a_2,a_3)$, $\mrm{B}(b_1,b_2,b_3)$に対し，線分$\mrm{AB}$を$m:n$に内分する点を$\mrm{P}$，$m:n$に外分する点を$\mrm{Q}$とすると，それぞれの座標は

$\begin{align*}&\mrm{P}\bra{\dfrac{na_1+mb_1}{m+n},\dfrac{na_2+mb_2}{m+n},\dfrac{na_3+mb_3}{m+n}}, \\&\mrm{Q}\bra{\dfrac{-na_1+mb_1}{m-n},\dfrac{-na_2+mb_2}{m-n},\dfrac{-na_3+mb_3}{m-n}}\end{align*}$