余弦定理は三平方の定理の進化形！例題からシンプルに理解する

三角比を用いた三角形の重要定理に正弦定理と余弦定理があります．

この記事では，三平方の定理の進化形ともいえる（第２）余弦定理を説明します．

余弦は$\cos$のことだったので，余弦定理は$\cos$に関する定理だということが名前から分かりますね．

この記事では

三平方の定理と余弦定理
余弦定理の具体例
余弦定理の証明
もうひとつの余弦定理（第１余弦定理）

を順に解説します．

「三角比」の一連の記事

三平方の定理と余弦定理
1. 三平方の定理の復習
2. 余弦定理
余弦定理の具体例
1. 例１（２辺の長さ・間の角の大きさが分かっている場合）
2. 例２（３辺の長さが分かっている場合）
余弦定理の証明
もうひとつの余弦定理（第１余弦定理）

三平方の定理と余弦定理

余弦定理の説明のために，まずは三平方の定理を確認しておきましょう．

三平方の定理の復習

三平方の定理は直角三角形の３辺の長さに関する定理なのでした．

［三平方の定理］$\ang{A}=90^{\circ}$の$\tri{ABC}$について，$a=\mrm{BC}$, $b=\mrm{CA}$, $c=\mrm{AB}$とする．

このとき，等式$a^{2}=b^{2}+c^{2}$が成り立つ．

余弦定理

三平方の定理は直角三角形には強い定理ですが，直角三角形でない場合には途端に使えなくなります．

この三平方の定理で$\ang{A}$が$90^\circ$でない場合にどうなるかを述べた定理が次の余弦定理です．

［余弦定理］$\tri{ABC}$について，$a=\mrm{BC}$, $b=\mrm{CA}$, $c=\mrm{AB}$とし，$\theta=\ang{A}$とおく．

このとき，等式

$\begin{align*}a^{2}=b^{2}+c^{2}-2bc\cos{\theta}\end{align*}$

が成り立つ．

$\ang{A}$が$90^\circ$から$\theta$に変わると，三平方の定理で成り立つ等式$a^{2}=b^{2}+c^{2}$が$-2bc\cos{\theta}$分だけズレるということになっているわけですね．

つまり，余弦定理が三平方の定理の拡張になっているわけですね．

ベクトルを学ぶと内積とも関連付けて考えることができて，更に覚えやすくなります．

余弦定理の具体例

余弦定理は３辺の長さと１つの内角の大きさが絡むときに使うことが多いです．

例１（２辺の長さ・間の角の大きさが分かっている場合）

$\mrm{AB}=2$, $\mrm{BC}=3$, $\ang{B}=120^\circ$の$\tri{ABC}$に対して，辺$\mrm{CA}$の長さを求めよ．

２つの辺の長さ・これらの辺の間の内角の大きさが分かっており，残る１辺の長さを求める問題です．

よって，３辺の長さと１つの内角の大きさが絡む問題なので，余弦定理がぴったりハマります．

余弦定理より，

$\begin{align*}\mrm{CA}^2&=\mrm{AB}^2+\mrm{BC}^2-2\mrm{AB}\cdot\mrm{BC}\cdot\cos{\ang{B}} \\&=4+9-2\cdot2\cdot3\cdot\cos{120^\circ} =19\end{align*}$

である．$\mrm{CA}>0$だから$\mrm{CA}=\sqrt{19}$を得る．

例２（３辺の長さが分かっている場合）

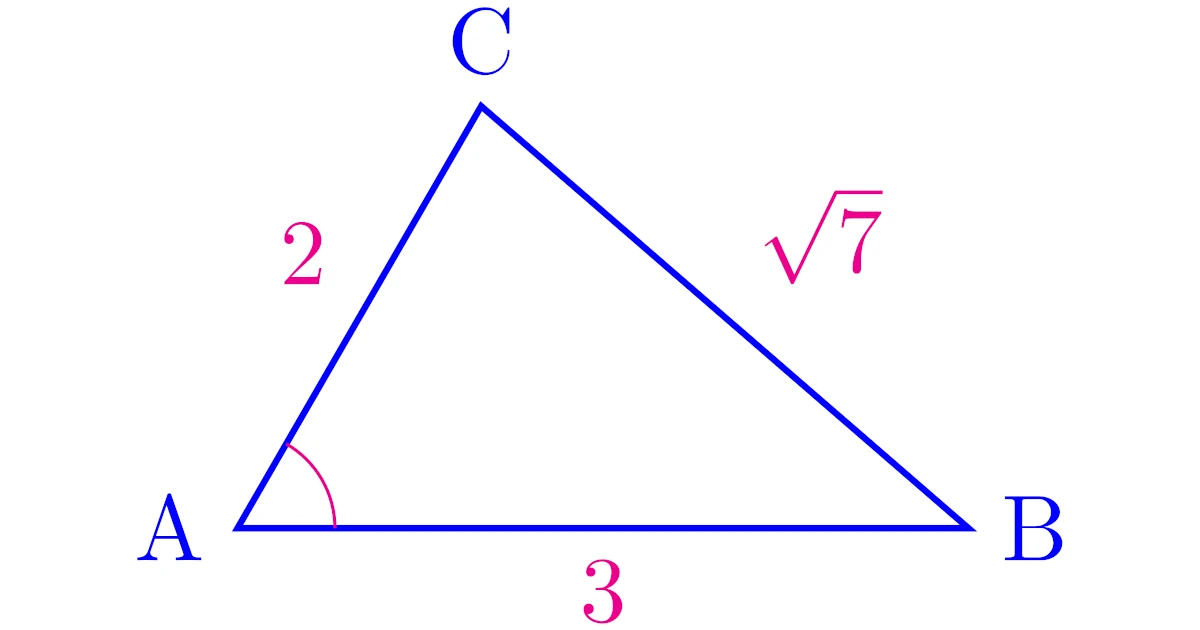
$\mrm{AB}=3$, $\mrm{BC}=\sqrt{7}$, $\mrm{CA}=2$の$\tri{ABC}$に対して，$\ang{A}$の大きさを求めよ．

３つの辺の長さが分かっており，１つの内角の大きさを求める問題です．

よって，３辺の長さと１つの内角の大きさが絡む問題なので，この問題も余弦定理から解くことができます．

余弦定理より，

$\begin{align*}&\mrm{BC}^2=\mrm{AB}^2+\mrm{CA}^2-2\mrm{AB}\cdot\mrm{CA}\cdot\cos{\ang{A}} \\&\iff 7=9+4-2\cdot2\cdot3\cdot\cos{\ang{A}} \\&\iff 12\cos{\ang{A}}=6 \iff \cos{\ang{A}}=\frac{1}{2} \\&\iff \ang{A}=60^\circ\end{align*}$

である．

余弦定理の証明

［余弦定理（再掲）］$\tri{ABC}$について，$a=\mrm{BC}$, $b=\mrm{CA}$, $c=\mrm{AB}$とし，$\theta=\ang{A}$とおく．

このとき，等式$a^{2}=b^{2}+c^{2}-2bc\cos{\theta}$が成り立つ．

$\ang{A}\leqq90^\circ$かつ$\ang{B}\leqq90^\circ$の場合
$\ang{A}>90^\circ$の場合
$\ang{B}>90^\circ$の場合

に分けて証明する．

$\ang{A}\leqq90^\circ$かつ$\ang{B}\leqq90^\circ$の場合の証明

頂点$\mrm{C}$から辺$\mrm{AB}$に下ろした垂線の足を$\mrm{H}$とする．

三角比の定義より$\mrm{AH}=b\cos{\theta}$, $\mrm{CH}=b\sin{\theta}$だから，$\tri{ABC}$で三平方の定理より，

$\begin{align*}a^2&=\mrm{BC}^2 =\mrm{CH}^2+\mrm{BH}^2 \\&=\mrm{CH}^2+(\mrm{AB}-\mrm{AH})^2 \\&=(b\sin{\theta})^2+(c-b\cos{\theta})^2 \\&=b^2\sin^2{\theta}+(c^2-2bc\cos{\theta}+b^2\cos^2{\theta}) \\&=b^2(\sin^2{\theta}+\cos^2{\theta})+c^2-2bc\cos{\theta} \\&=b^2+c^2-2bc\cos{\theta}\end{align*}$

が成り立つ．

$\ang{A}>90^\circ$の場合の場合の証明

頂点$\mrm{C}$から直線$\mrm{AB}$に下ろした垂線の足を$\mrm{H}$とする．

三角比の定義と（$180^\circ-\theta$）型の変換公式より

$\mrm{AH}=b\cos{(180^\circ-\theta)}=-b\cos{\theta}$
$\mrm{CH}=b\sin{(180^\circ-\theta)}=b\sin{\theta}$

なので，$\tri{AHC}$で三平方の定理より，

$\begin{align*}a^2&=\mrm{BH}^2+\mrm{CH}^2 =(\mrm{AB}+\mrm{AH})^2+\mrm{CH}^2 \\&=(c-b\cos{\theta})^2+(b\sin{\theta})^2 \\&=(c^2-2bc\cos{\theta}+b^2\cos^2{\theta})+b^2\sin^2{\theta} \\&=b^2(\sin^2{\theta}+\cos^2{\theta})+c^2-2bc\cos{\theta} \\&=b^2+c^2-2bc\cos{\theta}\end{align*}$

が成り立つ．

$\ang{B}>90^\circ$の場合の証明

頂点$\mrm{C}$から直線$\mrm{AB}$に下ろした垂線の足を$\mrm{H}$とする．

三角比の定義より$\mrm{AH}=b\cos{\theta}$, $\mrm{CH}=b\sin{\theta}$だから$\tri{BHC}$で三平方の定理より，

$\begin{align*}a^2&=\mrm{BH}^2+\mrm{CH}^2 =(\mrm{AH}-\mrm{AB})^2+\mrm{CH}^2 \\&=(b\cos{\theta}-c)^2+(b\sin{\theta})^2 \\&=(b^2\cos^2{\theta}-2bc\cos{\theta}+c^2)+b^2\sin^2{\theta} \\&=b^2(\cos^2{\theta}+\sin^2{\theta})+c^2-2bc\cos{\theta} \\&=b^2+c^2-2bc\cos{\theta}\end{align*}$