角度$\theta$の範囲を$0^\circ\le\theta\le180^\circ$まで拡張した三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$の重要な応用に正弦定理があります．
正弦定理は三角形の辺の長さ・角の大きさ・外接円の半径の関係についての定理で，とくに
- 向かい合う辺と角が絡む問題
- 三角形の外接円の半径が絡む問題
の２つのタイプの問題で有効にはたらくことが多いのがポイントです．
この記事では
- 正弦定理と具体例
- 三角形の外接円の半径を用いた面積公式
- 正弦定理の証明
を順に説明します．
「三角比」の一連の記事
正弦定理と具体例
そもそも正弦とは$\sin$のことをいうことを思い出すと，「正弦定理」という名前から$\sin$に関する定理であることが分かりますね．
正弦定理
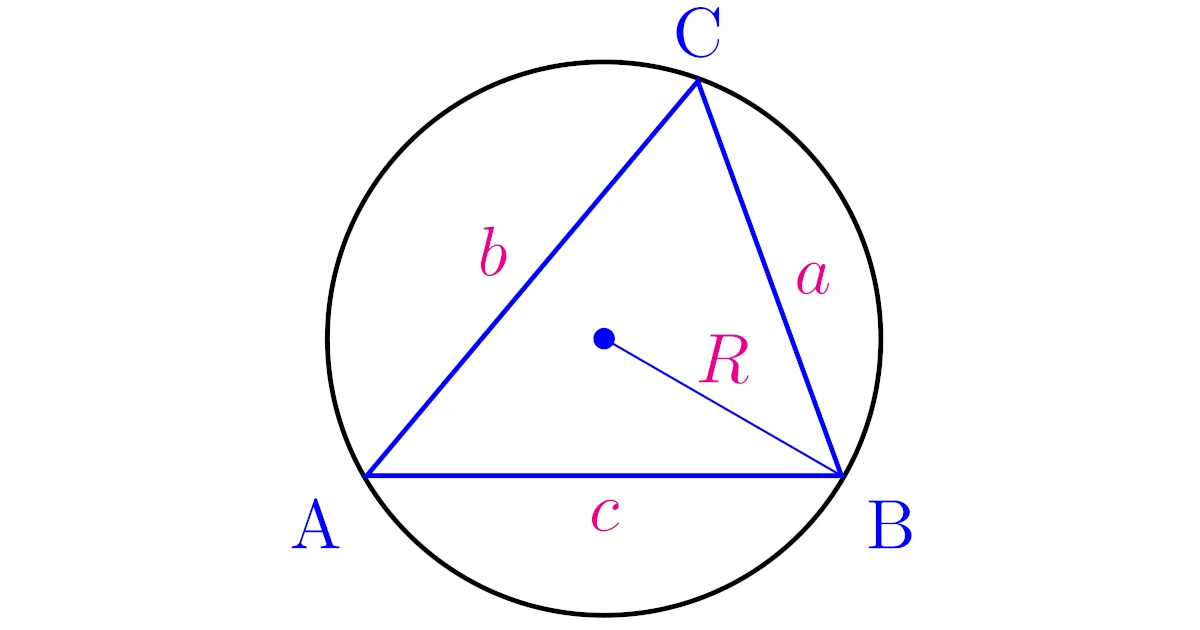
［正弦定理］$\tri{ABC}$について$a=\mrm{BC}$, $b=\mrm{CA}$, $c=\mrm{AB}$とおく．$\tri{ABC}$の外接円の半径が$R$のとき
\begin{align*}\frac{a}{\sin{\ang{A}}}=\frac{b}{\sin{\ang{B}}}=\frac{c}{\sin{\ang{C}}}=2R\end{align*}
が成り立つ．
正弦定理はこの記事の最後で証明します．
冒頭でも触れたように
- 向かい合う辺と角が絡む問題
- 三角形の外接円の半径が絡む問題
ので有効にはたらくことが多いです．
とくに(2)について「外接円の半径」という言葉を見たとき，正弦定理は第１候補として真っ先に考えたいくらい大切です．
以下では$a=\mrm{BC}$, $b=\mrm{CA}$, $c=\mrm{AB}$とし，$\tri{ABC}$の外接円の半径を$R$として，具体例を考えましょう．
具体例１（向かい合う辺と角から解ける問題）
$a=2$, $\sin{\ang{A}}=\dfrac{2}{3}$, $\sin{\ang{B}}=\dfrac{3}{4}$の$\tri{ABC}$に対して，$R$, $b$を求めよ．
向かい合う辺$\mrm{BC}$と角$\ang{A}$が絡む問題なので，正弦定理が見えたい問題です．
正弦定理より
\begin{align*}\frac{a}{\sin{\ang{A}}}=\frac{b}{\sin{\ang{B}}}
\iff&\frac{2}{2/3}=\frac{b}{3/4}
\\\iff&b=\frac{9}{4}\end{align*}
である．再び正弦定理より
\begin{align*}2R=\frac{a}{\sin{\ang{A}}}=\frac{2}{2/3}=3\end{align*}
なので$R=\dfrac{3}{2}$である．
正弦定理より$\dfrac{a}{\sin{\ang{A}}}=\dfrac{b}{\sin{\ang{B}}}$が成り立つので，$a$, $\sin{\ang{A}}$, $b$, $\sin{\ang{B}}$のうち３つが分かっていれば残るひとつが分かるわけですね．
また，正弦定理から$\dfrac{a}{\sin{\ang{A}}}=2R$も成り立つので外接円の半径$R$もすぐに得られますね．
具体例２（外接円の半径から解ける問題）
$a=2$, $\ang{B}=45^\circ$, $R=2$の$\tri{ABC}$に対して，$b$, $\ang{A}$を求めよ．
三角形の外接円の半径$R$が分かっているので，正弦定理が真っ先に見えたい問題です．
正弦定理より
\begin{align*}2R=\frac{b}{\sin{\ang{B}}}
\iff& 4=\frac{b}{\sin{45^\circ}}
\\\iff& 4=\frac{b}{\frac{1}{\sqrt{2}}}
\\\iff& b=2\sqrt{2}\end{align*}
である．再び正弦定理より
\begin{align*}2R=\frac{a}{\sin{\ang{A}}}
\iff& 4=\frac{2}{\sin{\ang{A}}}
\\\iff& \sin{\ang{A}}=\frac{1}{2}\end{align*}
なので$\ang{A}=30^\circ, 150^\circ$となる．
しかし，もし$\ang{A}=150^\circ$なら$\ang{B}=45^\circ$と併せて$\tri{ABC}$の内角の和が$180^\circ$を超えるから不適．一方，$\ang{A}=30^\circ$は適する．
正弦定理より$2R=\dfrac{b}{\sin{\ang{B}}}$が成り立つので，外接円の半径$R$が分かっていることと併せて，$b$, $\sin{\ang{B}}$の一方が分かれば他方が得られますね．
具体例３（２つの角の大きさから解ける問題）
$c=4$, $\ang{C}=45^\circ$, $\ang{B}=15^\circ$の$\tri{ABC}$に対して，$a$と$\tri{ABC}$の面積$S$を求めよ．
三角形の内角の大きさの和は$180^\circ$だから
\begin{align*}\ang{A}=180^\circ-\ang{B}-\ang{C}=120^\circ\end{align*}
なので，正弦定理より
\begin{align*}\frac{a}{\sin{\ang{A}}}=\frac{c}{\sin{\ang{C}}}
&\iff\frac{a}{\sin{120^\circ}}=\frac{4}{\sin{\ang{45^\circ}}}
\\&\iff\frac{a}{\sqrt{3}/2}=4\sqrt{2}
\\&\iff a=2\sqrt{6}\end{align*}
である．よって，三角形の$\sin$を用いた面積公式より
\begin{align*}S&=\frac{1}{2}bc\sin{A}
=\frac{1}{2}\cdot2(\sqrt{3}-1)\cdot4\cdot\sin{120^\circ}
\\&=\frac{1}{2}\cdot2(\sqrt{3}-1)\cdot4\cdot\frac{\sqrt{3}}{2}
=2\sqrt{3}(\sqrt{3}-1)\end{align*}
となる．
三角形の２つの内角の大きさが分かっている場合は，残る１つの内角の大きさも求められることは当たり前にしておきたいところです．
また，$\tri{ABC}=\dfrac{1}{2}bc\sin{A}$と三角形の面積が$\sin$を用いて表せることも思い出しておきましょう．
三角形の外接円の半径を用いた面積の公式
正弦定理を応用すると，$\tri{ABC}$の外接円の半径$R$と３辺の長さ$a$, $b$, $c$を用いた面積公式が証明できます．
$\tri{ABC}$について$a=\mrm{BC}$, $b=\mrm{CA}$, $c=\mrm{AB}$とおく．$\tri{ABC}$の外接円の半径が$R$のとき，$\tri{ABC}$の面積は
\begin{align*}\tri{ABC}=\frac{abc}{4R}\end{align*}
と表せる．
三角形の$\sin$を用いた面積公式より$\tri{ABC}$の面積は$\dfrac{1}{2}bc\sin{\ang{A}}$である．
正弦定理より$\sin{\ang{A}}=\dfrac{a}{2R}$が成り立つことと併せて
\begin{align*}\tri{ABC}
=\frac{1}{2}bc\sin{\ang{A}}
=\frac{1}{2}bc\cdot\frac{a}{2R}
=\frac{abc}{4R}\end{align*}
を得る．
正弦定理の証明
最後に正弦定理を証明しましょう．
円周角の定理の復習
正弦定理の証明のために円周角の定理（inscribed angle theorem）を思い出しておきましょう．
［円周角の定理］中心$\mrm{O}$の円周上の異なる２点$\mrm{A}$, $\mrm{C}$を考える．このとき，次が成り立つ．
- 直線$\mrm{AC}$に関して$\mrm{O}$と同じ側の円周上の任意の点$\mrm{B}$に対して，$2\ang{ABC}=\ang{AOC}$が成り立つ．
- 直線$\mrm{AC}$に関して同じ側にある円周上の任意の２点$\mrm{B}$, $\mrm{B’}$に対して，$\ang{ABC}=\ang{AB’C}$が成り立つ．
円周角の定理は
- $2\ang{ABC}=\ang{AOC}$を示す．
- これにより$\ang{ABC}=\dfrac{1}{2}\ang{AOC}=\ang{AB’C}$が示される
という２ステップで証明することができるのでした．
正弦定理の証明
それでは，正弦定理を証明しましょう．
［正弦定理（再掲）］$\tri{ABC}$について$a=\mrm{BC}$, $b=\mrm{CA}$, $c=\mrm{AB}$とおく．$\tri{ABC}$の外接円の半径が$R$のとき
\begin{align*}\frac{a}{\sin{\ang{A}}}=\frac{b}{\sin{\ang{B}}}=\frac{c}{\sin{\ang{C}}}=2R\end{align*}
が成り立つ．
$2R=\dfrac{a}{\sin{\ang{A}}}$を示すには分母を払った$2R\sin{\ang{A}}=a$を示せばよいですね．
$2R=\dfrac{a}{\sin{\ang{A}}}$, $2R=\dfrac{b}{\sin{\ang{B}}}$, $2R=\dfrac{c}{\sin{\ang{C}}}$を示せば良い．
これらは同様に示すことができるので，以下では
\begin{align*}2R=\dfrac{a}{\sin{\ang{A}}}\end{align*}
のみ示せば十分である．これを
- $0^\circ<\ang{A}<90^\circ$の場合
- $\ang{A}=90^\circ$の場合
- $90^\circ<\ang{A}<180^\circ$の場合
に分けて示す．
${0^\circ<\ang{A}<90^\circ}$の場合の証明
点Dを線分$\mrm{BD}$が外接円の直径となるようにとる．
このとき，$\ang{BCD}=90^\circ$なので
\begin{align*}\sin{\ang{D}}=\frac{\mrm{BC}}{\mrm{BD}}=\frac{a}{2R}\end{align*}
だから$2R\sin{\ang{D}}=a$であり，弧$\mrm{BC}$に関する円周角の定理より$\ang{A}=\ang{D}$だから，$2R\sin{\ang{A}}=a$が従う．
${\ang{A}=90^\circ}$の場合の証明
線分$\mrm{BC}$が外接円の直径となる．
よって，$2R=a$が成り立つ．$\ang{A}=90^\circ$なので，$\sin{\ang{A}}=1$だから$2R\sin{\ang{A}}=a$が成り立つ．
${90^\circ<\ang{A}<180^\circ}$の場合の証明
外接円の中心を点$\mrm{O}$とし，線分$\mrm{BD}$が外接円の直径となるように点$\mrm{D}$をとる．
このとき，$\ang{BCD}=90^\circ$なので，
\begin{align*}\sin{\ang{D}}=\frac{\mrm{BC}}{\mrm{BD}}=\frac{a}{2R}\end{align*}
だから$2R\sin{\ang{D}}=a$である．また，弧$\mrm{BC}$に関する円周角の定理より
\begin{align*}&2\ang{A}=\ang{BOC}(>180^\circ),
\\&2\ang{D}=\ang{BOC}(<180^\circ)\end{align*}
だから，$2\ang{A}+2\ang{D}=360^\circ$となり$\ang{D}=180^\circ-\ang{A}$が成り立つ．
三角比の$(180^\circ-\theta)$型の変換公式より，$\sin{\ang{D}}=\sin{180^\circ-\ang{A}}=\sin{\ang{A}}$なので，$2R\sin{\ang{A}}=a$を得る．
最後の$90^\circ<\ang{A}<180^\circ$のときの証明では，「四角形が外接四角形を持つための条件より$\ang{D}=180^\circ-\ang{A}$が成り立つ」としても構いません．
コメント