三角比sinθ,cosθ,tanθの角度θを90°以上に拡張する考え方

三角比
2019.03.30
三角比

直角三角形のひとつの鋭角を$\theta$として三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$を考えると，三角形の内角の和は$180^\circ$なので$\theta$は$0^\circ<\theta<90^\circ$の範囲でしか考えることができません．

Rendered by QuickLaTeX.com

そこで$\theta$の範囲をさらに拡張して三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$を定義しようというのが今回の記事の目標です．

「そんなこと考えて何になんの？」と思うかもしれませんが，鈍角三角形では内角が$90^\circ$以上になることもあるので，$\theta\geqq90^\circ$の場合に$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$が定義されていると便利なのです．

この記事では

  • 三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$の拡張
  • 拡張された三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$の性質

を順に説明します．

「三角比」の一連の記事

  1. 1 「三角比」とは何か？有名角の三角比も紹介
  2. 2 sin,cos,tanの相互関係を例題から理解する
  3. 3 「(90°-θ)型の変換公式」が当たり前になる考え方
  4. 4 sinθ,cosθ,tanθの角度θを90°以上でも考えたい (今の記事)
  5. 5 tanθの図形的な意味とxy平面上の直線の傾き
  6. 6 「(180°-θ)型の変換公式」は図から一瞬という話
  7. 7 正弦定理の２つのポイントを具体例から解説
  8. 8 余弦定理のコツを例題からシンプルに理解する

三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$の拡張

これまで学んできた直角三角形で定義される三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$の基本を確認して，$\theta$を$90^\circ$以上の場合に拡張しましょう．

三角比の基本図形

斜辺の長さが$1$の直角三角形のひとつの鋭角を$\theta$とするとき，斜辺でない２辺の長さが$\sin{\theta}$, $\cos{\theta}$と表せることは当たり前にしておきましょう．

$\mrm{AC}=1$, $\ang{B}=90^\circ$の直角三角形$\tri{ABC}$を考える．このとき，$\theta=\ang{A}$とすると，

   \begin{align*}\mrm{AB}=\cos{\theta},\quad \mrm{BC}=\sin{\theta}\end{align*}

が成り立つ．

Rendered by QuickLaTeX.com

三角比の定義より

   \begin{align*}\cos{\theta}=\frac{\mrm{AB}}{\mrm{AC}},\quad \sin{\theta}=\frac{\mrm{BC}}{\mrm{AC}}\end{align*}

であり，いま$\mrm{AC}=1$だから

   \begin{align*}\mrm{AB}=\cos{\theta},\quad \mrm{BC}=\sin{\theta}\end{align*}

が成り立つ．

一般的な呼称ではありませんが，私はこの図を三角比の基本図形と呼んでいます．三角比の定義から

   \begin{align*}\tan{\theta}=\frac{\mrm{BC}}{\mrm{AB}}=\frac{\sin{\theta}}{\cos{\theta}}\end{align*}

と三角比$\sin$, $\cos$, $\tan$の関係式がすぐに得られますし，三平方の定理から

   \begin{align*}\sin^2{\theta}+\cos^2{\theta}=1\end{align*}

と三角比$\sin$, $\cos$の関係式もすぐに得られますね．

また，図形を$r$倍に拡大すれば，斜辺が$r$の直角三角形の残りの２辺の長さが$r\sin{\theta}$, $r\cos{\theta}$と表せることもすぐに分かりますね．

Rendered by QuickLaTeX.com

三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$（${0^{\circ}\leqq\theta\leqq180^\circ}$）の定義

上で考えた三角比の基本図形を$xy$平面上に頂点$\mrm{A}$が原点，線分$\mrm{AB}$が$x$軸上，点$\mrm{C}$の$y$座標が正となるように下図のようにおきましょう．

Rendered by QuickLaTeX.com

このとき，点$\mrm{C}$の$x$座標は$\cos{\theta}$で，$y$座標が$\sin{\theta}$となりますね．

この図をふまえて$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$を$0^\circ\leqq\theta\leqq180^\circ$で定義しましょう．

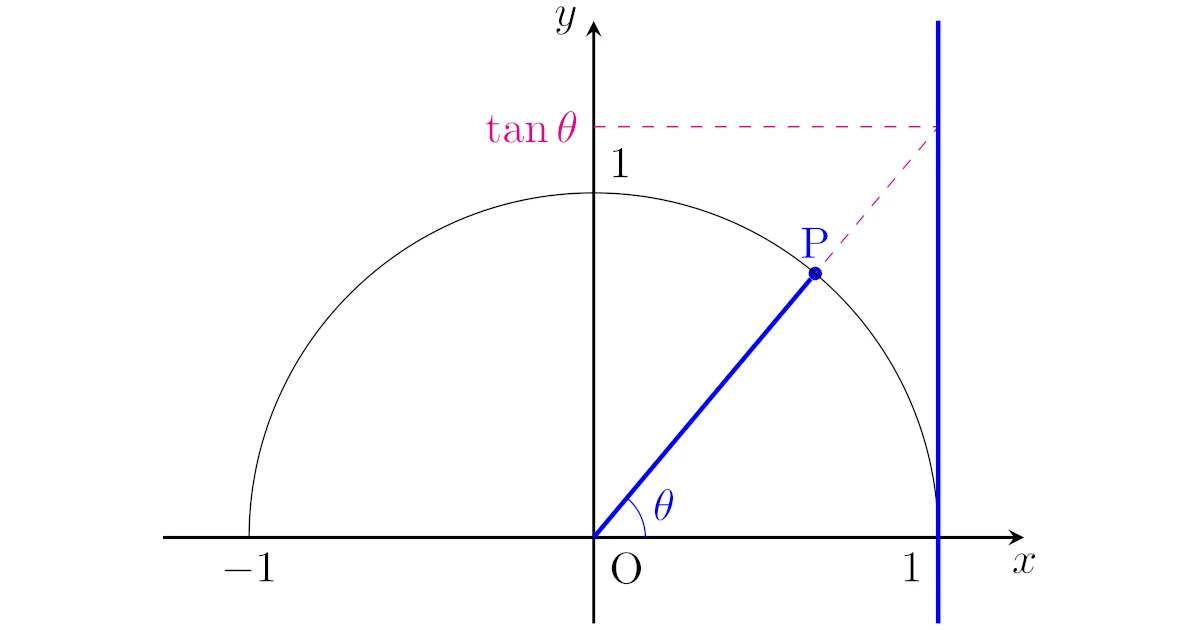
原点$\mrm{O}$の$xy$平面において，$y$座標が$0$以上の単位円上の点$\mrm{P}$，点$\mrm{A}(1,0)$を考える．$\theta=\ang{AOP}$とするとき，

  • $\mrm{P}$の$x$座標を$\cos{\theta}$
  • $\mrm{P}$の$y$座標を$\sin{\theta}$

と定める．また，$\cos{\theta}\neq0$のとき，$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$と定める．

Rendered by QuickLaTeX.com

直角三角形を用いて定義した三角比では，$\tan{\theta}$も辺の比で定義して関係式$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$を導きましたが，ここではこの式によって$\tan{\theta}$を定義しています．

このように定義すれば$0^\circ<\theta<90^\circ$のときは直角三角形で定義した三角比と矛盾せず，$0^{\circ}\leqq\theta\leqq180^\circ$の範囲にまで$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$が定義できるわけですね．

ただし，$\tan{\theta}$は$\cos{\theta}\neq0$のときに定義されるということに注意してください．

というのは，数学では０除算（０で割ること）はダメでしたから，$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$の分母は０であってはいけません．

そのため，$\tan{\theta}$は$\cos{\theta}\neq0$となる$\theta\neq90^\circ$の場合を除外して定義するわけですね．

三角比$\sin$, $\cos$, $\tan$の相互関係

先ほども少し触れましたが，$0^\circ<\theta<90^\circ$の場合に三角比の関係式

  1. $\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$
  2. $\cos^{2}{\theta}+\sin^{2}{\theta}=1$
  3. $1+\tan^{2}{\theta}=\dfrac{1}{\cos^{2}{\theta}}$
  4. $1+\dfrac{1}{\tan^{2}{\theta}}=\dfrac{1}{\sin^{2}{\theta}}$

が成り立つのでした．これらの等式は$0^\circ\leqq\theta\leqq180^\circ$の場合でも成り立ちます．

$0^\circ\leqq\theta\leqq180^\circ$を満たす実数$\theta$について，等式

  1. $\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$
  2. $\cos^{2}{\theta}+\sin^{2}{\theta}=1$
  3. $1+\tan^{2}{\theta}=\dfrac{1}{\cos^{2}{\theta}}$
  4. $1+\dfrac{1}{\tan^{2}{\theta}}=\dfrac{1}{\sin^{2}{\theta}}$

が成り立つ．ただし，(1)と(3)は$\cos{\theta}\neq0$のときに，(4)は$\sin{\theta}\neq0$かつ$\tan{\theta}\neq0$のときに成り立つ．

$0^\circ<\theta<90^\circ$のときは$\sin{\theta},\cos{\theta},\tan{\theta}$はいつでも正なので分母が$0$になるかどうかは気にしなくても問題ありませんでした．

しかし，$0^\circ\leqq\theta\leqq180^\circ$の場合には$\sin{\theta},\cos{\theta},\tan{\theta}$が$0$になることがあるので，３つ目と４つ目の関係式は分母が$0$にならないときのみ考えられますね．

$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$は$\tan{\theta}$の定義そのものである．

また，単位円周上の点$(\cos{\theta},\sin{\theta})$と原点$(0,0)$との距離は$1$だから，

   \begin{align*}&(\cos{\theta}-0)^2+(\sin{\theta}-0)^2=1^2 \\\iff&\cos^{2}{\theta}+\sin^{2}{\theta}=1\end{align*}

が成り立つ．

$\cos{\theta}\neq0$のとき，$\cos^{2}{\theta}+\sin^{2}{\theta}=1$の両辺を$\cos^{2}{\theta}$で割れば，

   \begin{align*}1+\tan^{2}{\theta}=\dfrac{1}{\cos^{2}{\theta}}\end{align*}

$\sin{\theta}\neq0$かつ$\cos{\theta}\neq0$のとき，$\cos^{2}{\theta}+\sin^{2}{\theta}=1$の両辺を$\sin^{2}{\theta}$で割れば，

   \begin{align*}\dfrac{1}{\tan^{2}{\theta}}+1=\dfrac{1}{\sin^{2}{\theta}}\end{align*}

が得られる．

コメント