根号について,次の問題に正しく答えられますか?
実数$a$に対して,$\sqrt{a^2}$の根号$\sqrt{\quad}$を外せ.
$\sqrt{a^2}=a$というのは間違いですよ.
これが正しく言えなければ,例えば$\sqrt{3-2\sqrt{2}}=\sqrt{2}-1$といった二重根号を外すときにも間違いをしかねません.
この記事では
- 平方根と根号の基本
- 二重根号の外し方
を順に説明します.
平方根と根号の基本
まずは平方根と根号の定義を確認しておきましょう.
$0$以上の実数$a$に対して,$2$乗して$a$となる実数を$a$の平方根という.
例えば,$4$の平方根は$2$乗して$4$になる実数なので$\pm2$ですね.
正の実数に対して平方根は必ず正負の2つ存在し, $0$の平方根は$0$のみですね.
$0$以上の実数$a$に対して,$a$の$0$以上の平方根を$\sqrt{a}$と表す.この記号$\sqrt{\quad}$を根号といい,$\sqrt{a}$を「ルート$a$」と読む.
例えば,$3$の$0$以上の平方根を$\sqrt{3}$と表すので,$3$の平方根は$\pm\sqrt{3}$ですね.
「$0$以上の平方根を$\sqrt{a}$と表す」と定義することから分かるように,$0$以上の実数$a$に対して$\sqrt{a}$が負になることはありません.
平方根と根号の性質
次の平方根と根号の性質は当たり前にしておきましょう.
次が成り立つ.
- 実数$a$が$0$以上の実数$b$の平方根なら,$-a$も$b$の平方根である.
- 正の実数$a$に対して,$(\sqrt{a})^2=a$
- 正の実数$a$, $b$に対して,$\sqrt{ab}=\sqrt{a}\sqrt{b}$が成り立つ.
(1)実数$a$が$b$の平方根であることから$a^2=b$が成り立つ.よって,$(-a)^2=a^2=b$が成り立つので$-a$も$b$の平方根である.
(2)$\sqrt{a}$は$a$の平方根の1つだから$2$乗すると$a$となる.すなわち,$(\sqrt{a})^2=a$が成り立つ.
(3)$\sqrt{a}\sqrt{b}$は正の数であり,(2)より$(\sqrt{a}\sqrt{b})^2=(\sqrt{a})^2(\sqrt{b})^2=ab$が成り立つ.よって,$\sqrt{a}\sqrt{b}$は$ab$の正の平方根なので,$\sqrt{ab}=\sqrt{a}\sqrt{b}$が成り立つ.
2乗の平方根
ここで冒頭の問題について,実数$a$に対して$\sqrt{a^2}$は次のようになります.
実数$a$に対して
\begin{align*}\sqrt{a^2}=\begin{cases}a&(a\ge0)\\-a&(a<0)\end{cases}\end{align*}
が成り立つ.
つまり,$a$の正負によりどのように根号$\sqrt{\quad}$が外れるか変わるわけですね.
以下で証明しますが,根号$\sqrt{a^2}$の定義は「$a^2$の$0$以上の平方根」だったことに注意しましょう.
[1]$a\ge0$のときには$a$を$2$乗すると$a^2$なので,$a$は$a^2$の$0$以上の平方根である.
よって,$\sqrt{a^2}=a$である.
[2]$a<0$のときには$-a>0$で,$-a$を$2$乗すると$a^2$なので,$-a$は$a^2$の$0$以上の平方根である.
よって,$\sqrt{a^2}=-a$である.
繰り返しますが,大切なことは根号が$0$以上の平方根を表すという点ですね.
例えば,$\sqrt{3^2}$と$\sqrt{(-3)^2}$の根号を上の公式を用いて外すと
- $\sqrt{3^2}$は公式で$a\geqq0$の場合に相当するので$\sqrt{3^2}=3$
- $\sqrt{(-3)^2}$は公式で$a<0$の場合に相当するので$\sqrt{(-3)^2}=-(-3)=3$
となります.実際,きちんと計算すれば,確かに
\begin{align*}&\sqrt{3^2}=\sqrt{9}=3,
\\&\sqrt{(-3)^2}=\sqrt{9}=3\end{align*}
となりますね.
上の公式の右辺は絶対値$|a|$と全く同じですから,$\sqrt{a^2}$は次のようにもすっきり表すことができますね.
実数$a$に対して,$\sqrt{a^2}=|a|$が成り立つ.
絶対値について詳しくは以下の記事を参照してください.

絶対値の定義から一瞬で解ける問題
二重根号
根号$\sqrt{\quad}$の中に根号$\sqrt{\quad}$が入ったものを二重根号と言いますが,
\begin{align*}\sqrt{3-2\sqrt{2}}=\sqrt{2}-1\end{align*}
のように二重根号は外せる場合があります.
二重根号を外すには,実数$A$, $B$に対して$\sqrt{(A\pm B)^2}=|A\pm B|$が成り立つことを用います.
実数$a$, $b$に対して,
\begin{align*}\sqrt{(a+b)\pm2\sqrt{ab}}=|\sqrt{a}\pm \sqrt{b}|\end{align*}
が成り立つ(複号同順).ただし,左辺の根号の中は$0$以上であるとする.
$(a+b)\pm2\sqrt{ab}=(\sqrt{a}\pm\sqrt{b})^2$なので,
\begin{align*}\sqrt{(a+b)\pm2\sqrt{ab}}=|\sqrt{a}\pm\sqrt{b}|\end{align*}
が従う.
具体例
いくつか具体例を考えてみましょう.
例1
$\sqrt{3+2\sqrt{2}}$の二重根号を外せ.
$3=2+1$, $2\sqrt{2}=2\sqrt{2\cdot1}$なので,
\begin{align*}\sqrt{3+2\sqrt{2}}
=&\sqrt{(2+1)+2\sqrt{2\cdot1}}
\\=&\sqrt{(\sqrt{2})^2+2\cdot\sqrt{2}\cdot1+1^2}
\\=&\sqrt{(\sqrt{2}+1)^2}
=\sqrt{2}+1\end{align*}
となる.ただし,最後の等式では,$\sqrt{2}+1>0$であることに注意.
例2
$\sqrt{7+4\sqrt{3}}$の二重根号を外せ.
$7=3+4$, $4\sqrt{3}=2\sqrt{12}=2\sqrt{3\cdot4}$なので,
\begin{align*}\sqrt{7+4\sqrt{12}}
=&\sqrt{(3+4)+2\sqrt{3\cdot4}}
\\=&\sqrt{(\sqrt{3})^2+2\cdot\sqrt{3}\cdot2+2^2}
\\=&\sqrt{(\sqrt{3}+2)^2}
=\sqrt{3}+2\end{align*}
となる.ただし,最後の等式では,$\sqrt{3}+2>0$であることに注意.
例3
$\sqrt{3-\sqrt{5}}$の二重根号を外せ.
$\sqrt{3-\sqrt{5}}=\sqrt{\dfrac{6-2\sqrt{5}}{2}}$であり,$6=5+1$, $2\sqrt{5}=2\cdot\sqrt{5\cdot1}$なので,
\begin{align*}\sqrt{3-\sqrt{5}}
=&\sqrt{\frac{(5+1)-2\sqrt{5\cdot1}}{2}}
\\=&\frac{\sqrt{(\sqrt{5})^2-2\cdot\sqrt{5}\cdot1+1^2}}{\sqrt{2}}
\\=&\frac{\sqrt{(\sqrt{5}-1)^2}}{\sqrt{2}}
=\frac{\sqrt{5}-1}{\sqrt{2}}
\\=&\frac{\sqrt{2}\bra{\sqrt{5}-1}}{2}\end{align*}
となる.ただし,$\sqrt{5}-1>0$であることに注意.
二重根号でありがちなミス
上の例3で
\begin{align*}\sqrt{5-2\sqrt{2}}
=&\sqrt{(\sqrt{2})^2-2\times\sqrt{3}\times\sqrt{2}+(\sqrt{3})^2}
\\=&\sqrt{(\sqrt{2}-\sqrt{3})^2}
=\sqrt{2}-\sqrt{3}\end{align*}
とするミスがよくあるのですが,どこが間違いが分かりますか?
間違いは根号を外すときで,$\sqrt{2}-\sqrt{3}<0$ですから,
\begin{align*}\sqrt{(\sqrt{2}-\sqrt{3})^2}
=&|\sqrt{2}-\sqrt{3}|
\\=&-(\sqrt{2}-\sqrt{3})
\\=&\sqrt{3}-\sqrt{2}\end{align*}
とするのが正しいですね.
$\sqrt{a^2}=|a|$を思い出しましょう.
このように,$\sqrt{a^2}=|a|$に注意できていれば,
\begin{align*}\sqrt{(\sqrt{2}-\sqrt{3})^2}
=&|\sqrt{2}-\sqrt{3}|
\\=&-(\sqrt{2}-\sqrt{3})\end{align*}
としようが,
\begin{align*}\sqrt{(\sqrt{3}-\sqrt{2})^2}
=&|\sqrt{3}-\sqrt{2}|
\\=&\sqrt{3}-\sqrt{2}\end{align*}
としようが同じ結果になります.
上の例3の解答で最後に根号$\sqrt{\quad}$の中身の正負に言及しているのは,このように根号$\sqrt{\quad}$を外すときにそのまま外すのかマイナスをつけて外すか変わってくるためです.
このように,二重根号を外す際には根号の中身の正負に注意するようにしてください.
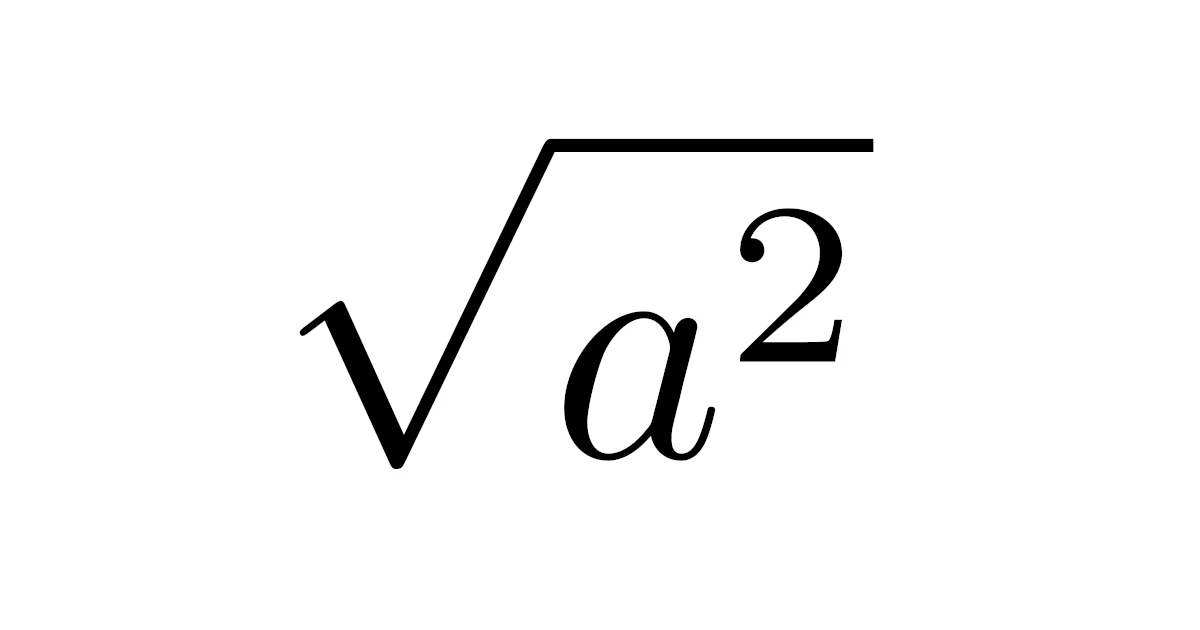
コメント