図形と方程式４
一般の直線の方程式と平行条件・垂直条件

図形と方程式
2016.03.19
図形と方程式

前回の記事では$xy$平面上の傾きをもつ２直線の平行条件・垂直条件について説明しました．

しかし，$xy$平面上の直線には$y=ax+b$の形の方程式で表せない（つまり，傾きをもたない）直線もあります．

そこで，$y=ax+b$では表せない直線も併せて表せる直線の方程式を一般の直線の方程式といいます．

この記事では，

  • 軸に平行な直線
  • 一般の直線の方程式
  • 平行条件と垂直条件

を説明します．

「図形と方程式」の一連の記事

  1. 1 座標の超基本「内分点」「外分点」の計算
  2. 2 「方程式が表すグラフ」ってそもそも何？
  3. 3 直線の傾きと平行条件・垂直条件
  4. 4 一般の直線の方程式の平行条件・垂直条件 (今の記事)
  5. 5 点と直線の距離の考え方と公式を理解する
  6. 6 ２種類の円の方程式をマスターしよう
  7. 7 円と直線の共有点の個数の２つの判定法
  8. 8 円の接線の方程式を一発で求める公式
  9. 9 ２円の共有点を通る直線・円はこう求めよ！

軸に平行な直線

前回の記事で説明したように，$y$軸に平行でない直線を傾きをもつ直線といい，傾きをもつ直線は

    \begin{align*}y=mx+c\end{align*}

の形の方程式で表すことができ，この$x$の係数$m$を傾きというのでした．

Rendered by QuickLaTeX.com

例えば，$y=x+1$, $y=-2x+5$はいずれも傾きをもつ直線ですね．

傾きをもつ直線は中学数学以来扱ってきたので馴染み深いですね．

図形と方程式３
直線の「傾き」の考え方と平行条件・垂直条件
１次関数$y=ax+b$のグラフはxy平面上の傾きをもつ直線になります．２つの直線y=ax+b,y=a'x+b'があるとき，これらの傾きに注目すると，これら２直線が平行か垂直かを判定することができます．
yama-taku.science

$x$軸に平行な直線の方程式

$x$軸に平行な直線は傾きをもつ（傾きが$0$の）直線として理解することができます．

$xy$平面上の２点$\mrm{A}(1,2)$, $\mrm{B}(5,2)$を通る直線$\ell_1$の方程式を求めよ．

Rendered by QuickLaTeX.com

直線$\ell_1$は２点$\mrm{A}(1,2)$, $\mrm{B}(5,2)$を通るから，傾きは

    \begin{align*}\frac{2-2}{5-1}=0\end{align*}

である．よって，前回の記事で説明したように直線$\ell_1$の方程式は

    \begin{align*}&y=0(x-1)+2 \\\iff&y=2\end{align*}

となる．

この解答では傾きが$0$をもつ直線と捉えていますが，次のように考えるともっと簡単に$y=2$が得られます．

そもそも$x,y$の方程式を満たす$(x,y)$を全て$xy$平面上に図示したものをグラフというのでした．

いま直線$\ell_1$が２点$\mrm{A}(1,2)$, $\mrm{B}(5,2)$を通ることから，直線$\ell_1$は$y$座標が$2$の点を全て通り，なおかつ$y$座標が$2$でない点は通らないので，方程式は$y=2$とすぐに分かりますね．

$y$軸に平行な直線の方程式

いまの考え方を踏まえると，$y$軸に平行な直線は次のように表せます．

$xy$平面上の２点$\mrm{A}(-3,2)$, $\mrm{B}(-3,4)$を通る直線$\ell_2$の方程式を求めよ．

Rendered by QuickLaTeX.com

２点$\mrm{A}(-3,2)$, $\mrm{B}(-3,4)$を通る直線$\ell_2$は$x$座標が$-3$の点を全て通り，$x$座標が$-3$でない点を通らない．

よって，直線の方程式は$x=-2$である．

問題からも分かるように，$y$軸に平行な直線は$x=a$の形の方程式で表されることが分かりますね．

一般の直線の方程式

いまみたように

  • 傾きをもつ直線は$y=mx+c$と表す
  • 傾きをもたない直線は$x=a$と表す

というのでは，どちらか分からない場合は場合分けが必要になり少々面倒ですね．

一般の直線の方程式

そこで，これらをどちらも表せる方程式を一般の直線の方程式といい，次のようになります．

$xy$平面上の任意の直線は，少なくとも一方は$0$でない実数$a$, $b$と，任意の実数$c$を用いて

    \begin{align*}ax+by+c=0\end{align*}

の形の方程式で表される．

この形の直線の方程式を一般の直線の方程式といいます．

例えば，$ax+by+c=0$で

  • $(a,b,c)=(-2,1,3)$とすれば$y=2x-3$
  • $(a,b,c)=(0,1,-2)$とすれば$y=2$
  • $(a,b,c)=(1,0,3)$とすれば$x=-3$

が得られますね．

このように，$ax+by+c=0$は$y=mx+c$の形にも$x=c$の形にもなりうるので，「一般の」直線の方程式というわけですね．

「$a$, $b$の少なくとも一方は$0$でない」という条件があるのは，$a=b=0$なら$c=0$となって直線を表さない式になってしまうためです．

$x$軸切片と$y$軸切片

$xy$平面上の直線$\ell$に対して，

  • 直線$\ell$と$x$軸との交点の$x$座標を$x$軸切片
  • 直線$\ell$と$y$軸との交点を$y$座標を$y$軸切片

という．

傾きのある直線の方程式$y=mx+c$の$c$を単に切片と言ってきましたが，詳しくは$y$軸切片というわけですね．

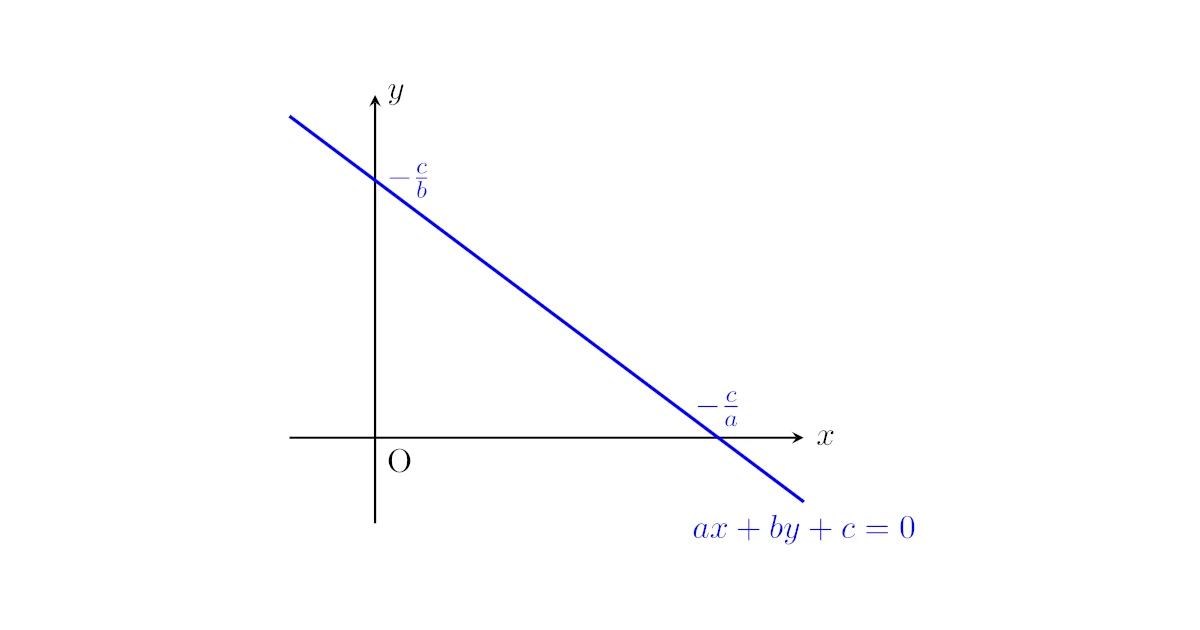
$x$軸にも$y$軸にも平行でない直線の方程式$ax+by+c=0$に対して，$a\neq0$かつ$b\neq0$のときは

  • $x=0$なら$y=-\dfrac{c}{b}$
  • $y=0$なら$x=-\dfrac{c}{a}$

となるので，$y$軸切片は$-\dfrac{c}{b}$で，$x$軸切片は$-\dfrac{c}{a}$ですね．

Rendered by QuickLaTeX.com

一般に次が成り立つことを知っておくと便利です．

$A,B$はどちらも$0$でない実数とする．$x,y$の方程式$\dfrac{x}{A}+\dfrac{y}{B}=1$の$xy$平面上のグラフは

  • $x$軸切片は$A$
  • $y$軸切片は$B$

である．

これは実際に$(x,y)=(A,0)$と$(x,y)=(0,B)$が方程式を満たすことから分かりますね．

平行条件と垂直条件

傾きをもつ２直線の平行条件・垂直条件については前回の記事で説明しましたね．

図形と方程式３
直線の「傾き」の考え方と平行条件・垂直条件
１次関数$y=ax+b$のグラフはxy平面上の傾きをもつ直線になります．２つの直線y=ax+b,y=a'x+b'があるとき，これらの傾きに注目すると，これら２直線が平行か垂直かを判定することができます．
yama-taku.science

一般の直線の方程式に対しても，平行条件・垂直条件は次のように与えられます．

[平行条件・垂直条件]　$xy$平面上の２直線$\ell_1:a_1x+b_1y+c_1=0$, $\ell_2:a_2x+b_2y+c_2=0$に対して，次が成り立つ．

  • $\ell_1$と$\ell_2$は平行である $\iff a_1b_2=a_2b_1$
  • $\ell_1$と$\ell_2$は垂直である $\iff a_1a_2=-b_1b_2$

平行条件・垂直条件はそれぞれ

  • 平行条件：$a_1:b_1=a_2:b_2$
  • 垂直条件：$a_1:b_1=(-b_2):a_2$

と表すこともできますね．

比$A:B$は$A,B$がどちらか一方が$0$でなければ定義される（分数は分母が$0$なら定義されない）ので，この意味では分数よりも扱いやすいです．

具体例

まずは具体的に使い方を見てみましょう．

$xy$平面上の次の直線の方程式を求めよ．

  1. $3x+5y=2$に平行で点$(1,2)$を通る直線$\ell_1$
  2. $-3x+6y=5$に垂直で点$(3,4)$を通る直線$\ell_2$

(1)　直線$\ell_1$は$(1,2)$を通るから$A(x-1)+B(y-2)=0$とおける．

さらに，直線$\ell_1$は$3x+5y=2$に平行だから，平行条件より$A:B=3:5$なので$A=3k$, $B=5k$ ($k$は$0$でない実数)とおける．

よって，$\ell_1$の方程式は

    \begin{align*} &3k(x-1)+5k(y-1)=0 \\\iff&3(x-1)+5(y-1)=0 \\\iff&3x+5y-8=0 \end{align*}

である．

(2)　直線$\ell_2$は$(3,4)$を通るから$A(x-3)+B(y-4)=0$とおける．

さらに，直線$\ell_2$は$-3x+6y=5$に垂直だから，垂直条件より$A:B=6:\{-(-3)\}=2:1$なので，$A=2k$, $B=k$ ($k$は$0$でない実数)とおける．

よって，$\ell_2$の方程式は

    \begin{align*} &2k(x-1)+k(y-1)=0 \\\iff&2(x-1)+(y-1)=0 \\\iff&2x+y-3=0 \end{align*}

である．

この解答のように，平行条件・垂直条件を比で扱うと便利なことも多いです．

係数比で理解する方法はベクトルを学ぶとより深く理解できますが，この記事ではここまでの説明に留めます．

証明

最後に平行条件・垂直条件を証明しましょう．

[平行条件・垂直条件（再掲）]　$xy$平面上の２直線$\ell_1:a_1x+b_1y+c_1=0$, $\ell_2:a_2x+b_2y+c_2=0$に対して，次が成り立つ．

  • $\ell_1$と$\ell_2$は平行である $\iff a_1b_2=a_2b_1$
  • $\ell_1$と$\ell_2$は垂直である $\iff a_1a_2=-b_1b_2$

[平行条件]　$\ell_1$と$\ell_2$が平行であるとする．

(i)$b_1=0$なら直線$\ell_1$は$y$軸に平行である．よって，直線$\ell_2$も$y$軸に平行なので$b_2=0$となる．

これらより，$a_1b_2=0$, $a_2b_1=0$なので$a_1b_2=a_2b_1$が成り立つ．

(ii)$b_1\neq0$なら直線$\ell_1$は$y$軸に平行でないから，直線$\ell_2$も$y$軸に平行でないので$b_2\neq0$となる．

これらより$\ell_1:y=-\dfrac{a_1}{b_1}x-\dfrac{c_1}{b_1}$, $\ell_2:y=-\dfrac{a_2}{b_2}x-\dfrac{c_2}{b_2}$となるから，傾きをもつ直線の平行条件より

    \begin{align*}-\dfrac{a_1}{b_1}=-\dfrac{a_2}{b_2}\iff a_1b_2=a_2b_1\end{align*}

が成り立つ．

逆に，$a_1b_2=a_2b_1$が成り立つとする．

(i’)$b_1=0$なら直線$a_1b_2=0$であり，$a_1$, $b_1$は同時に$0$にはならないから$b_2=0$である．

よって，$\ell_1$と$\ell_2$はどちらも$y$軸に平行だから，$\ell_1$と$\ell_2$は平行である．

(ii’)$b_1\neq0$なら直線$\ell_1$は$y$軸に平行でないから，直線$\ell_2$も$y$軸に平行でないので$b_2\neq0$となる．

これらより$\ell_1:y=-\dfrac{a_1}{b_1}x-\dfrac{c_1}{b_1}$, $\ell_2:y=-\dfrac{a_2}{b_2}x-\dfrac{c_2}{b_2}$となり，$a_2=\dfrac{a_1b_2}{b_1}$と併せて

    \begin{align*}-\frac{a_2}{b_2}=-\frac{1}{b_2}\cdot\frac{a_1b_2}{b_1}=-\frac{a_1}{b_1}\end{align*}

が成り立つから，傾きをもつ直線の平行条件より$\ell_1$と$\ell_2$は平行である．

[垂直条件]　(i)$b_1=0$のとき，(ii)$a_1=0$のとき，(iii)$a_1\neq0$かつ$b_1\neq0$のときに場合分けする．

(i), (ii)では$\ell_1$, $\ell_2$がそれぞれどの軸に平行かを考えて，(ii)では傾きをもつ直線の垂直条件を用いれば証明できる．

考え方は平行条件と同じなので，詳しくは読者に任せる．

コメント