微分の２つの定義式｜図から同じであることを理解しよう

関数$f(x)$の$x=a$での微分係数$f'(a)$は$y=f(x)$のグラフの接線の傾きをもとにして定義されます．

この微分係数$f'(a)$の定義式は

$\lim\limits_{b\to a}\dfrac{f(b)-f(a)}{b-a}$
$\lim\limits_{h\to0}\dfrac{f(a+h)-f(a)}{h}$

のどちらかで書かれることが多いのですが，どちらも本質的には全く同じでもちろん計算結果も等しくなります．

この記事では

２つの微分係数の定義の関係
２つの定義の具体例

を順に説明します．

微分法１
微分係数とは？$y=f(x)$のグラフの接線を求めよう！

「微分法」を用いることで，例えばxy平面上のy=2x³のグラフのx=-1での接線の方程式を求めることができます．この記事では接線の方程式の求め方をテーマに，微分係数の定義と使い方を説明します．

２つの微分係数の定義
２つの定義で計算する

２つの微分係数の定義

冒頭の２つの微分係数の定義を比較しましょう．

微分係数の定義１

[定義１]　関数$f(x)$と実数$a$に対して，極限

$\begin{align*}\lim_{b\to a}\dfrac{f(b)-f(a)}{b-a}\end{align*}$

が存在するとき，$f(x)$は$x=a$で微分可能であるという．また，この極限を「関数$f(x)$の$x=a$における微分係数」といい，$f'(a)$と表す．

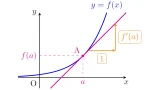
この[定義１]の図形的イメージは以下の通りです．

$xy$平面上に点$\mrm{A}(a,f(a))$と異なる$y=f(x)$上の点$\mrm{B}(b,f(b))$を考えます．

このとき，$b\to a$とすれば直線$\mrm{AB}$は曲線$y=f(x)$上の点$\mrm{A}$での接線に近付きます．

そのため，直線$\mrm{AB}$の傾き

$\begin{align*}\frac{f(b)-f(a)}{b-a}\end{align*}$

は極限$b\to a$をとれば曲線$y=f(x)$上の点$\mrm{A}$での接線の傾きに近付くので，極限$\lim\limits_{b\to a}\dfrac{f(b)-f(a)}{b-a}$が曲線$y=f(x)$上の点$\mrm{A}$での接線の傾きとなるわけですね．

微分係数の定義２

[定義２]　関数$f(x)$と実数$a$に対して，極限

$\begin{align*}\lim_{h\to 0}\dfrac{f(a+h)-f(a)}{h}\end{align*}$

が存在するとき，$f(x)$は$x=a$で微分可能であるという．また，この極限を「関数$f(x)$の$x=a$における微分係数」といい，$f'(a)$と表す．

この[定義２]の図形的イメージは以下の通りです．

$h$を実数とすると，$xy$平面上に点$\mrm{A}(a,f(a))$と異なる$y=f(x)$上の点$\mrm{B}(a+h,f(a+h))$をとることができます．

このとき，$h\to0$とすれば直線$\mrm{AB}$は曲線$y=f(x)$上の点$\mrm{A}$での接線に近付きます．

そのため，直線$\mrm{AB}$の傾き

$\begin{align*}\frac{f(a+h)-f(a)}{h}\bra{=\frac{f(a+h)-f(a)}{(a+h)-a}}\end{align*}$

は極限$h\to0$をとれば曲線$y=f(x)$上の点$\mrm{A}$での接線の傾きに近付くので，極限$\lim\limits_{h\to 0}\dfrac{f(a+h)-f(a)}{h}$が曲線$y=f(x)$上の点$\mrm{A}$での接線の傾きとなるわけですね．

２つの定義式が等しいこと

以上の考え方から[定義１]と[定義２]では文字は違うものの，同じ図を考えていることが分かります．

[定義１]では２点$(a,f(a)),(b,f(b))$を通る直線の傾きをもとに考えて，[定義２]では２点$(a,f(a)),(a+h,f(a+h))$を通る直線の傾きをもとに考えています．

このことから，[定義１]と[定義２]は$b=a+h$という関係で移り合うことが分かりますね．

実際，[定義１]の

$\begin{align*}\lim_{b\to a}\dfrac{f(b)-f(a)}{b-a}\end{align*}$

で$b=a+h$とおくと

極限$b\to a$は
$\begin{align*}b\to a\iff& a+h\to a\\\iff& h\to 0\end{align*}$
平均変化率$\dfrac{f(b)-f(a)}{b-a}$は
$\begin{align*}\frac{f(b)-f(a)}{b-a}=\frac{f(a+h)-f(a)}{h}\end{align*}$

となるので，

$\begin{align*}&\lim_{b\to a}\frac{f(b)-f(a)}{b-a} =\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}\end{align*}$

と確かに[定義２]に等しくなることがわかりますね．

２つの定義で計算する

いまみたように[定義１]の定義式と[定義２]の定義式が同じであることから，どちらの定義でも同じ結果になるはずです．

このことを具体的にみてみましょう．

$f(x)=x^3$の$x=2$での微分係数を[定義１]と[定義２]の両方で求めよ．

[定義１]によると

$\begin{align*}\lim_{b\to 2}\frac{f(b)-f(2)}{b-2} =&\lim_{b\to 2}\frac{b^3-2^3}{b-2} \\=&\lim_{b\to 2}\frac{(b-2)(b^2+2b+2^2)}{b-2} \\=&\lim_{b\to 2}(b^2+2b+2^2) \\=&2^2+2\times2+2^2=3\times 2^2=12\end{align*}$

である．また，[定義２]によると

$\begin{align*}\lim_{h\to0}\frac{f(2+h)-f(2)}{h} =&\lim_{h\to0}\frac{(2+h)^3-2^3}{h} \\=&\lim_{h\to0}\frac{(2^3+3\times2^2h+3\times2h^2)-h^3}{h} \\=&\lim_{h\to0}\frac{3\times2^2h+3\times2h^2}{h} \\=&\lim_{h\to0}(3\times2^2+3\times2h)=3\times 2^2=12\end{align*}$