数学IAでは三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$について，(90°-θ)型の公式と(180°-θ)型の公式が成り立つことを学びました．
数学IIBで学ぶ三角関数$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$では$\theta$が実数全体を動くので，$\tan{(180^\circ+\theta)}$や$\sin{(90^\circ+\theta)}$などの変換も扱えるようになる必要があります．
教科書ではそのような公式がたくさん並んでいて「これらを覚えないといけないのか……」と考えてしまう方は多いのですが，実はそのうちのほとんどの公式は覚える必要はありません！
分かりやすい公式を少し覚えておくだけで，他の偏角の変換公式は全て導けるようになっています．
今回の記事では
- ３タイプの基本の変換公式
- 他の変換公式の導き方
を順に説明します．
「三角関数」の一連の記事
３タイプの基本の変換公式
以下の三角関数の公式は図を考えればすぐに分かります．まずはこれらを理解しましょう．
実数$\theta$に対して，次が成り立つ．
- $\begin{cases}\cos{(\theta\pm180^{\circ})}=-\cos{\theta}\\\sin{(\theta\pm180^{\circ})}=-\sin{\theta}\end{cases}$
- $\begin{cases}\cos{(-\theta)}=\cos{\theta}\\\sin{(-\theta)}=-\sin{\theta}\end{cases}$
- $\begin{cases}\cos{(90^{\circ}-\theta)}=\sin{\theta}\\\sin{(90^{\circ}-\theta)}=\cos{\theta}\end{cases}$
これらの公式は全部で
- タイプ１：$(\theta\pm180^{\circ})$型の公式
- タイプ２：$(-\theta)$型の公式
- タイプ３：$(90^{\circ}-\theta)$型の公式
の３タイプですね．以下では，点Oを原点，点Pを単位円周上の偏角$\theta$の点$(\cos{\theta},\sin{\theta})$とします．
タイプ１：$(\theta\pm180^\circ)$型の公式
単位円周上の点Pと原点対称な点をQとすると，点Qの偏角は$\theta+180^\circ$, $\theta-180^\circ$のどちらとも言えるので，点Qの座標は
\begin{align*}\mrm{Q}(\cos{(\theta\pm180^{\circ})},\sin{(\theta\pm180^{\circ})})\end{align*}
ですね．
点Pと点Qについて$x$座標も$y$座標もともに正負が逆になっているので，$(\theta\pm180^{\circ})$型の公式
\begin{align*}\cos{(\theta\pm180^{\circ})}=-\cos{\theta},\quad
\sin{(\theta\pm180^{\circ})}=-\sin{\theta}\end{align*}
が得られますね．
タイプ２：$(-\theta)$型の公式
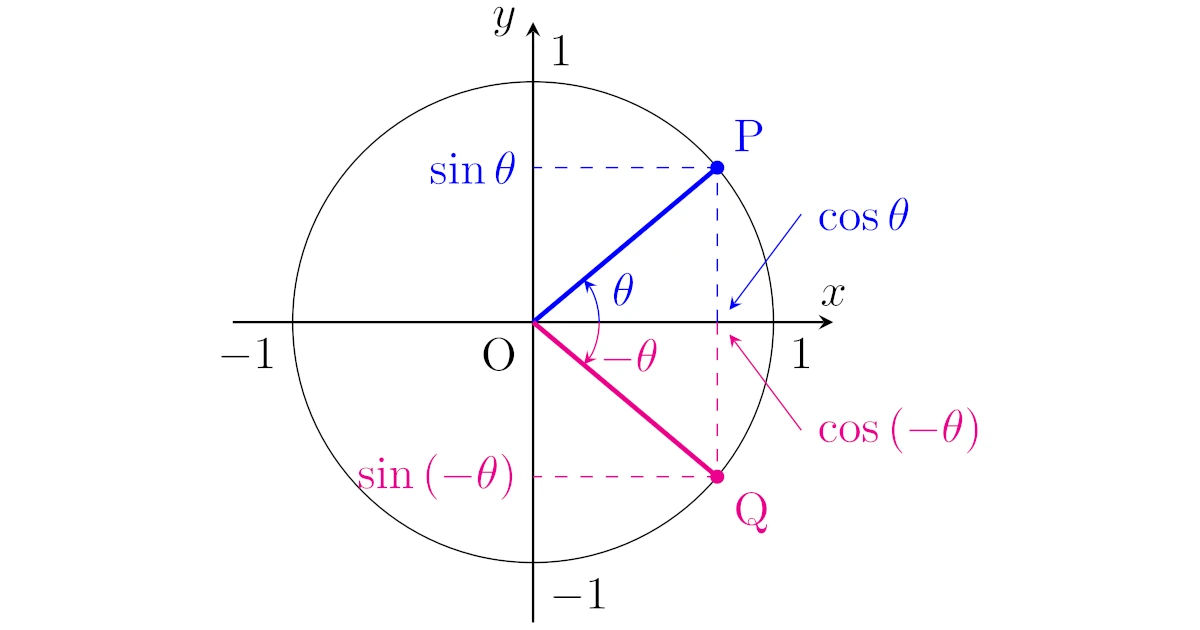
単位円周上の点Pと$x$軸対称な点をQとすると，点Qの偏角は$-\theta$なので，点Qの座標は
\begin{align*}\mrm{Q}(\cos{(-\theta)},\sin{(-\theta)})\end{align*}
ですね．
点Pと点Qについて$x$座標は等しく，$y$座標は正負が逆になっているので，$(-\theta)$型の公式
\begin{align*}\cos{(-\theta)}=\cos{\theta},\quad
\sin{(-\theta)}=-\sin{\theta}\end{align*}
が得られますね．
タイプ３：$(90^\circ-\theta)$型の公式
$0<\theta<90^\circ$の三角比の場合に(90°-θ)型の公式の変換公式が成り立つことは数学IAで学びました．ここでも確認しておきましょう．
$\ang{A}=\theta$, $\ang{B}=90^{\circ}$の直角三角形$\tri{ABC}$を考えると，$\ang{C}=90^{\circ}-\theta$ですね．
よって，三角比の定義から
\begin{align*}&\cos{\theta}=\frac{\mrm{AB}}{\mrm{AC}}=\sin{(90^\circ-\theta)},
\\&\sin{\theta}=\frac{\mrm{BC}}{\mrm{AC}}=\cos{(90^\circ-\theta)}\end{align*}
が得られますね．
この証明は$0<\theta<90^\circ$の場合のみの証明となっていますが，任意の実数$\theta$に対して成り立つことも証明できます（この証明はこの記事の最後を参照）．
他の変換公式の導き方
他のタイプの偏角の変換公式は，上でみた３タイプの基本の変換公式から導けます．
（再掲）実数$\theta$に対して，次が成り立つ．
- $\begin{cases}\cos{(\theta\pm180^{\circ})}=-\cos{\theta}\\\sin{(\theta\pm180^{\circ})}=-\sin{\theta}\end{cases}$
- $\begin{cases}\cos{(-\theta)}=\cos{\theta}\\\sin{(-\theta)}=-\sin{\theta}\end{cases}$
- $\begin{cases}\cos{(90^{\circ}-\theta)}=\sin{\theta}\\\sin{(90^{\circ}-\theta)}=\cos{\theta}\end{cases}$
以下でいくつか具体的に求めてみましょう．以下のものくらいなら慣れれば数秒で導けるようになります．
変換公式の例１（$\cos(-180^{\circ}-\theta)$）
$\cos(-180^{\circ}-\theta)$を簡単にせよ．
$(\theta-180^\circ)$型の変換公式と$(-\theta)$型の変換公式を使います．
\begin{align*}\cos(-180^{\circ}-\theta)=-\cos(-\theta)=-\cos{\theta}\end{align*}
変換公式の例２（$\sin(\theta-90^{\circ})$）
$\sin(\theta-90^{\circ})$を簡単にせよ．
$90^\circ$が絡む場合は$(90^\circ-\theta)$型の公式に持ち込むのが鉄板です．
\begin{align*}\sin(\theta-90^{\circ})&=\sin\{-(90^{\circ}-\theta)\}
\\&=-\sin(90^{\circ}-\theta)=-\cos{\theta}\end{align*}
変換公式の例３（$\sin(90^{\circ}+\theta)$）
$\sin(90^{\circ}+\theta)$を簡単にせよ．
今回も$90^\circ$が絡むので，やはり$(90^\circ-\theta)$型の公式を使います．
\begin{align*}\sin(90^{\circ}+\theta)&=\sin\{90^{\circ}-(-\theta)\}
\\&=\cos(-\theta)=\cos{\theta}\end{align*}
変換公式の例４（$\tan(180^{\circ}-\theta)$）
$\tan(180^{\circ}-\theta)$を簡単にせよ．
$\tan$の変換公式は$\tan$の定義$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$を用いて$\sin$, $\cos$を使って表してから，それぞれで変換公式を使えば良いですね．
\begin{align*}\tan(180^{\circ}-\theta)&=\dfrac{\sin{(180^{\circ}-\theta)}}{\cos{(180^{\circ}-\theta)}}
\\&=\dfrac{\sin{(-\theta)}}{\cos{(-\theta)}}=\dfrac{-\sin{\theta}}{\cos{\theta}}=-\tan{\theta}\end{align*}
一般の場合の$(90^\circ-\theta)$型の公式の証明
先ほどの$(90^\circ-\theta)$型の公式
\begin{align*}\cos{(\theta+90^{\circ})}=-\sin{\theta},\quad
\sin{(\theta+90^{\circ})}=\cos{\theta}\end{align*}
は$0<\theta<90^\circ$の三角比の場合のものでしたから，任意の$\theta$に対しても成り立つことを示しておきましょう．
（再々掲）実数$\theta$に対して，次の$(90^{\circ}-\theta)$型の公式が成り立つ．
\begin{align*}\begin{cases}\cos{(90^{\circ}-\theta)}=\sin{\theta}\\\sin{(90^{\circ}-\theta)}=\cos{\theta}\end{cases}\end{align*}
さまざまな証明方法がありますが，ここでは$(-\theta)$型の変換公式と合わせることで示しましょう．
単位円周上の偏角$-\theta$の点Pを原点中心に$90^\circ$回転させた点をQとすると，点Qの座標は
\begin{align*}\mrm{Q}(\cos{(\theta+90^{\circ})},\sin{(\theta+90^{\circ})})\end{align*}
である．
この図で線分OP，線分OQを斜辺とする２つの直角三角形の合同を考えて，
\begin{align*}\cos{(90^{\circ}-\theta)}=-\sin{(-\theta)},\quad
\sin{(90^{\circ}-\theta)}=\cos{(-\theta)}\end{align*}
が成り立つ．$(-\theta)$型の変換公式と併せて
\begin{align*}\cos{(90^{\circ}-\theta)}=\sin{\theta},\quad
\sin{(90^{\circ}-\theta)}=\cos{\theta}\end{align*}
と$(90^\circ-\theta)$型の変換公式が得られる．
このように一般の実数$\theta$の場合の証明は少し手間ですが，直角三角形の場合を考えれば公式自体を覚えるのは簡単ですね．
コメント