張力の基本<br>滑車があっても怖くない！<br>シンプルに理解しよう

張力は教科書でもあまり大きな扱われ方がされないためか，張力をなんとなくで捉えてしまっている人が多くいる印象を受けます．

しかし，高校物理で張力は頻出ですから，きっちり理解して使えるようになっておく必要があります．

例えば，糸を両側から引っ張ると両側に力が働きますが，このときはたらく張力は両側で等しいです．

また，張力に関する問題で迷う人が多いのは滑車が関わってくる問題ですが，滑車が関わってくる場合でも張力の考え方はいたってシンプルです．

この記事では基本的な張力の考え方を説明し，具体例を用いて張力の求め方の例もみていきます．

張力

ここでは

まっすぐ糸を引く場合
滑車にかけて糸を引く場合

の２つに分けて基本の事実を整理しておきましょう．

まっすぐ糸を引く場合

例えば，糸の端が物体に繋がっているとき，糸を引っ張ると糸は物体を引きます．

このように，「それほど弾力のない糸が物体を引く力」を張力といいます．

この張力については次の事実が重要です．

[張力]　糸がピンと張られた状態で，糸の両端で張力の大きさは等しい．

例えば，下図のように物体Aと物体Bがピンと張られた糸で繋がっているとき，「糸が物体Aを引く張力」と「糸が物体Bを引く張力」は同じ大きさで，向きは逆になります．

滑車を通して糸を引く場合

滑車が絡む場合の張力については，次の[滑車]が成り立ちます．

[滑車]　滑車に糸がかかっているとき，糸が滑車を引く張力の大きさは滑車の両側で等しい．

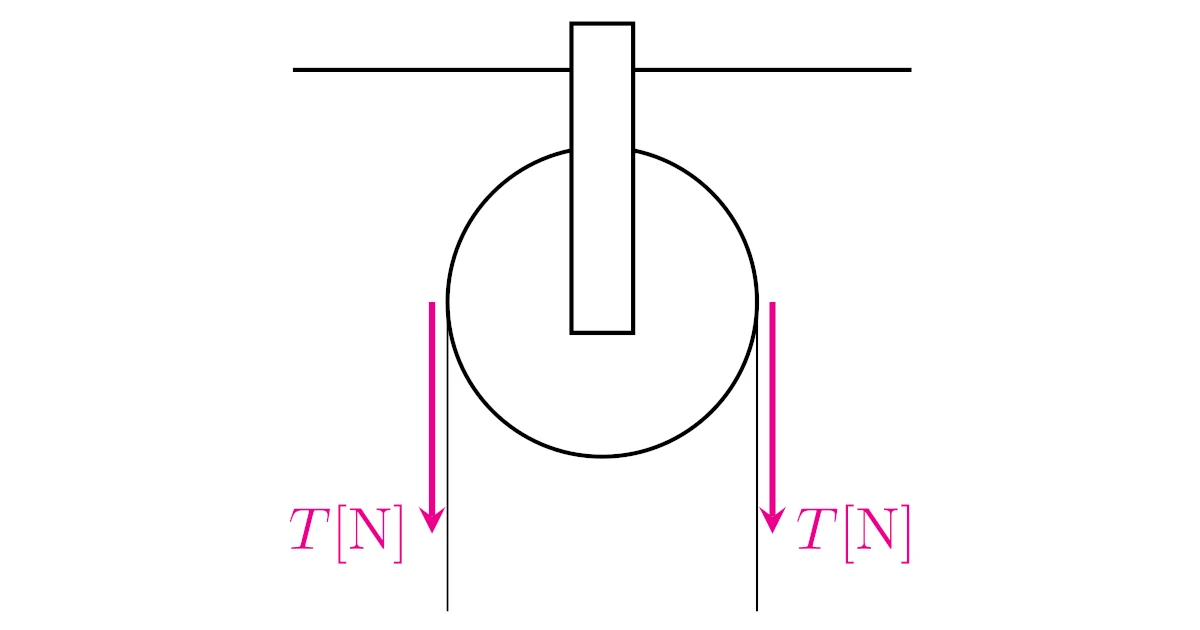
例えば，下図のように天井に留めた滑車に糸をかけて下から引くとき，「滑車の右から出ている糸が引く張力」と「滑車の右から出ている糸が引く張力」は同じ大きさです．

なお，実際には滑車が動くときには「右の張力の大きさ」と「左の張力の大きさ」はほんの少しだけ異なります．

しかし，過剰に速く動かすのでない限りこの誤差は無視できるほど小さいので，高校物理では「滑車を引く張力の大きさはどちらも同じ」とするのが普通です．

張力の例

さて，上で見た２つの事実[張力]，[滑車]をもとに，具体例で張力の考え方を見ていきましょう．

例１(単純な張力)

質量$m[\mrm{kg}]$の物体を天井から１本の糸で吊るすと物体は静止した．

このとき，糸が物体を引っ張る張力の大きさを求めよ．ただし，重力加速度の大きさを$g[\mrm{m/s^{2}}]$とする．

このとき，天井と物体は糸から張力を受けて引っ張られます．[基本]からこの張力の大きさは等しく，この張力の大きさを$T[\mrm{N}]$としましょう．

また，物体の質量が$m[\mrm{kg}]$，重力加速度が$g[\mrm{m/s^2}]$なので，物体には鉛直下向きに大きさ$mg[\mrm{N}]$の重力がはたきます．

これらを図に書き込むと下図のようになります．

物体は静止していることから，物体にはたらく力はつりあっているので，つりあいの条件から

$\begin{align*} T-mg=0 \iff T=mg \end{align*}$

となり，糸が物体を引っ張る張力の大きさが$mg[N]$と分かりました．

【力の基本２｜力のつりあいとその例】

物体にはたらく全ての力を合わせた力が0になっていることを「力がつりあっている」といい，力がつりあっている物体は速度を変えず運動を続けます．つまり，静止している物体は静止し続け，等速直線運動をしている物体はそのまま等速直線運動を続けます．

例２(滑車が回らない場合)

質量$M[\mrm{kg}]$の物体A，質量$m[\mrm{kg}]$の物体Bを１本の糸で繋ぎ，糸を天井に固定された滑車にかけると，物体Aは地面で静止し，物体Bは糸で吊られて静止した．

このときの糸が物体Aを引っ張る張力の大きさと物体Aが床から受ける垂直抗力の大きさを求めよ．ただし，重力加速度の大きさを$g[\mrm{m/s^{2}}]$，$M>m$とする．

滑車は左右の糸から張力を受けて引っ張られ，物体A, Bも糸から張力を受けて引っ張られます．上で説明した２つの事実からこの張力の大きさは等しいので，この張力の大きさを$T[\mrm{N}]$としましょう．

また，物体A, Bの質量がそれぞれ$M[\mrm{N}]$, $m[\mrm{N}]$，重力加速度が$g[\mrm{m/s^{2}}]$なので，物体A, Bにはそれぞれ鉛直下向きに大きさ$Mg[\mrm{N}]$, $mg[\mrm{N}]$の重力がはたきます．

さらに，忘れ図に物体Aが床から受ける垂直抗力の大きさを$N[\mrm{N}]$としましょう．

２つの物体が接しているときには，必ず垂直抗力と摩擦がはたらいていないか注意する癖をつけておきましょう．

これらを図に書き込むと下図のようになります．

$m>M$より物体Aの方が重く，物体Aと物体Bは静止し続けるので，物体にはたらく力はつりあっています．よって，つりあいの条件から

$\begin{align*} \begin{cases} T+N-Mg=0\\ T-mg=0 \end{cases} \iff\begin{cases} T=mg\\ N=(M-m)g \end{cases} \end{align*}$

となります．

以上より

糸が物体Aを引っ張る張力の大きさは$mg[\mrm{N}]$
物体Aが床から受ける垂直抗力の大きさ張力の大きさは$(M-m)g[\mrm{N}]$

と分かりました．

糸で物体Aを持ち上げようと物体Bが反対側から大きさ$mg[\mrm{N}]$の重力で引っ張っているので，糸で吊り上げられていないときの$A$が受けるはずの垂直抗力の$Mg[\mrm{N}]$よりも$mg[\mrm{N}]$分だけ持ち上げられ，垂直抗力が$(M-m)g[\mrm{N}]$となっているわけですね．

例３(滑車が回る場合)

質量$M[\mrm{kg}]$の物体A，質量$m[\mrm{kg}]$の物体Bを１本の糸で繋ぎ，糸を天井に固定された滑車にかけると，物体A，物体Bはともに糸で吊られた状態になった．

このときの糸が物体Aを引っ張る張力の大きさと物体Aの加速度の大きさを求めよ．ただし，重力加速度の大きさを$g[\mrm{m/s^{2}}]$，$M>m$とする．

例２では物体Aの質量の方が大きかったのが，例３では物体Bの質量の方が大きくなりました

例２と同じく，滑車が左右の糸から受ける張力，物体A, Bが糸から受ける張力の大きさは等しく，この張力の大きさを$T[\mrm{N}]$としましょう．

また，物体A, Bには鉛直下向きに大きさ$mg[\mrm{N}]$, $Mg[\mrm{N}]$の重力がそれぞれはたきます．

しかし，今回は物体Bの方が重いので，物体Bが滑車を通して物体Aを吊り上げていくため，物体Aに垂直抗力はかかりません．

このとき，物体Aが上昇する加速度と物体Bが下降する加速度の大きさは等しく，これを$a[\mrm{m/s^{2}}]$としましょう．

これらを図に書き込むと下図のようになります．

物体Aは大きさ$a[\mrm{m/s^{2}}]$の加速度で上昇し，物体B大きさ大きさ$a[\mrm{m/s^{2}}]$の加速度で下降するから，運動方程式から

$\begin{align*} \begin{cases} T-mg=ma\\ Mg-T=Ma \end{cases} \iff\begin{cases} T=\dfrac{2mM}{m+M}g\\ a=\dfrac{M-m}{M+m}g \end{cases} \end{align*}$

となりますね．以上より

糸が物体Aを引っ張る張力の大きさは$\dfrac{2mM}{m+M}g[\mrm{N}]$
物体Aの加速度の大きさは$\dfrac{M-m}{M+m}g[\mrm{N}]$

と分かりました．

張力の$\dfrac{2mM}{m+M}$の部分は$\dfrac{2}{\frac{1}{M}+\frac{1}{m}}$と変形できますが，これを$m$と$M$の調和平均と言います．

一般に，$n$個の正の数$a_1,\dots,a_n$に対して，$\dfrac{n}{\frac{1}{a_1}+\dots+\frac{1}{a_n}}$を$a_1,\dots,a_n$の調和平均と言います．

物理や数学には，調和平均がいろいろなところに顔を出すので，注意してみると面白いかもしれませんね．