質点の場合とは異なり,剛体にはたらく力については,力の大きさ・向きに加えて力の作用点を考えることが大切なのでした.
そのため,剛体にはたらく重力の作用点を知ることは大切です.
均一な球などは中心に重力がはたらく(とみなせる)ことは自然ですが,次の問題のような対称でない形をした剛体にはたらく重力の作用点はどのように考えれば良いでしょうか?
半径5の円板から,下図のように半径2の円板をくり抜いた板$D$にはたらく重力の作用点を求めよ.
この記事では
- 重心とは何か?
- 重心の具体例
を順に説明します.
「剛体の運動」の一連の記事
重心とは何か?
円板の中心に糸をつけて糸で吊るすと,円板は水平の状態で静止することを我々は経験から知っています.
よって,剛体にはたらく力のつりあいを考えると
- 円板にはたらく重力
- 糸による張力
がつりあっていることが分かります.このことから,円板にはたらく重力の作用点は円板の中心と「みなせる」ことになりますね.
重心の定義
いま「みなせる」と書いたのには理由があります.
実際には重力は円板の中心にのみ重力がはたらいているわけではなく,円板の至る部分に重力ははたらいています.
ところが,それらの重力を剛体にはたらく力の合成として全て併せると,円板の中心に重力がはたらいていると考えてよいわけですね.
このように,重力の作用点とみなせる点を重心といいます.
剛体にはたらく重力の合力の作用点を,その剛体の重心という.
数学では「三角形の重心」を習いますが,均質な三角形の板の「物理的な重心」は「数学的な重心」に一致します.
重心の性質
重心がどことみなせるかについては,次の[事実]が大切です.
剛体が線対称な図形であれば,その対称の軸上に重心が存在する.
対称の軸上に重心が存在するという[事実]からも,上で考えた「円板にはたらく重力の作用点は円板の中心」を導いておきましょう.
円板の中心Oを通る直線$\ell$を引くと,円板は$\ell$を軸として線対称ですから,上の[事実]から円板の重心は直線$\ell$上にあります.
同様に,円板の中心Oを通る$\ell$とは異なる直線$\ell’$を引くと,直線$\ell’$を軸として線対称ですから,円板の重心は直線$\ell’$上にあります.
さて,円板の重心は直線$\ell$上にあり,かつ直線$\ell’$上にあることが分かりました.
直線$\ell$上かつ直線$\ell’$上にある点は中心Oですから,円板の重心は中心Oであることが分かりました.
重心の具体例
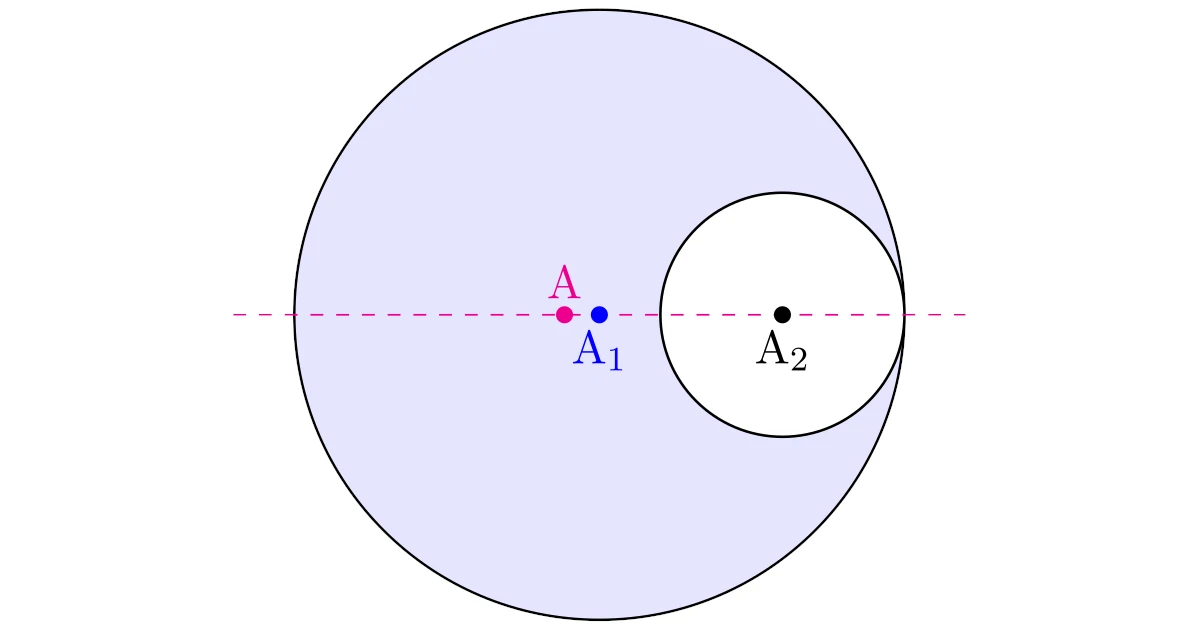
半径5の円板から,下図のように半径2の円板をくり抜いた板$D$にはたらく重力の作用点を求めよ.
まず$D$は線対称な図形なので,[事実]から$D$の重心が対称の軸上にあることはすぐに分かりますね.
もとの半径5の円板を$D_1$,くり抜いた半径2の円板を$D_2$とし
- $D$の重心を$\mrm{A}$
- もとの円板$D_1$の重心を$\mrm{A}_1$
- くり抜いた円板$D_2$の重心を$\mrm{A}_2$
とすると,$\mrm{A}_1$は$D_1$の中心,$\mrm{A}_2$は$D_2$の中心ですね.
$D_1$と$D_2$の相似比は$5:2$なので,$D_1$と$D_2$の面積比は$25:4$ですから,
- $\mrm{A}_1$にはたらく$D_1$の重力の大きさ
- $\mrm{A}_2$にはたらく$D_2$の重力の大きさ
- $\mrm{A}$にはたらく$D$の重力の大きさ
の比は$25:4:21$となります.また,$D$と$D_2$を組み合わせると$D_1$になるので,$D$にはたらく重力と$D_2$にはたらく重力の合力の作用点は$\mrm{A}_1$となります.
よって,剛体にはたらく力の合成を考えて,$\mrm{A}$は線分$\mrm{A_1A_2}$を$4:25$に外分する点と分かりました.
コメント