次の問題はどのように解きますか?
実数$x$, $y$が$x+y=3$, $xy=1$を満たすとき,$x^4+y^4$の値を求めよ.
「$x+y=3$, $xy=1$を連立方程式だと思って,$x$, $y$を求めて代入!」という方法でも確かに解けますが,実際に$x$, $y$を求めると
なので,これを$x^4+y^4$に代入して計算するのはかなり面倒です.
そこで上手い方法を考えたいわけですが,$x^4+y^4$が対称式であることを利用する方法があります.
この記事では
- 対称式とは何か?
- 対称式を利用する問題
- 3次以上の対称式
を順に解説します.
対称式とは何か?
まずは対称式について基本事項を解説します.
対称式の定義と重要性質
$x$, $y$の多項式が対称式であるとは,$x$と$y$を入れ替えても元の多項式に等しい多項式のことをいう.
「$x$, $y$の多項式$f(x,y)$が対称式であるとは,$f(x,y)=f(y,x)$が成り立つことをいう」といっても同じことですね.
例えば
などはいずれも$x$, $y$の対称式です.例えば
といった具合ですね.
さて,$x$, $y$の対称式の中でも$x+y$, $xy$は基本対称式とよばれる特別な対称式です.
この2つの対称式がどのように特別かというと,実は次の定理が成り立ちます.
任意の$x$, $y$の対称式は基本対称式$x+y$, $xy$の和,差,積で表すことができる.
この定理から基本対称式は対称式の基本単位であるといえますね.
この定理はとても強力で,この定理を背景とした問題は大学入試でも頻出です.
3文字以上の多項式についても対称式は定義されますが,これについてはこの記事の最後を参照してください.
基本対称式で対称式を表す例
それでは実際に$x$, $y$の対称式をいくつか基本対称式$x+y$, $xy$の和,差,積で表してみましょう.
次の$x$, $y$の対称式を基本対称式$x+y$, $xy$の和,差,積で表せ.
- $x^2+y^2$
- $(x-y)^2$
- $x^3+y^3$
(1) $(x+y)^2$を展開すると,$(x+y)^2=x^2+2xy+y^2$なので,$2xy$を移項して
と$x^2+y^2$が基本対称式$x+y$, $xy$の和,差,積で表せる.
(2) $(x-y)^2$を展開すると,$(x-y)^2=x^2-2xy+y^2$であり,(1)と併せると
と$(x-y)^2$が基本対称式$x+y$, $xy$の和,差,積で表せる.
(3) $(x+y)^3$を展開すると,$(x+y)^3=x^3+3x^2y+3xy^2+y^3$なので,$3x^2y+3xy^2$を$3xy$でくくって移項して
と$x^3+y^3$が基本対称式$x+y$, $xy$の和,差,積で表せる.
対称式を利用する問題
次の問題は対称式を用いる典型的な問題です.
$t$の方程式$t^2-3t+1=0$の2解を$x$, $y$とするとき,次の値を求めよ.
- $x^2y+x^2y$
- $x^2+y^2$
- $x^4+y^4$
この問題ではいずれの多項式も対称式なので「$x+y$と$xy$が求まるのではないか」と考えたいところです.
2次方程式の解と係数の関係から$x+y$, $xy$の値が求まるので,対称式であることを利用しましょう.
解と係数の関係から,$x+y=3$, $xy=1$である.
(1) $x^2y+x^2y=xy(x+y)$だから,この右辺に$x+y$, $xy$を代入して
である.
(2) $x^2+y^2=(x+y)^2-2xy$だから,この右辺に$x+y$, $xy$を代入して
である.
(3) $(x+y)^4=x^4+4x^3y+6x^2y^2+4xy^3+y^4$だから,$4x^3y+6x^2y^2+4xy^3$を移項して
である.この右辺に$x+y$, $xy$と(2)で求めた$x^2+y^2$を代入して
である.
$x$, $y$を具体的に求めて代入するよりもよっぽど速いですね.
この問題のように,解と係数の関係と絡めて対称式が出題されることはよくあるので,意識しておくと気付きやすいでしょう.
3変数以上の対称式
3変数以上でも同様に対称式が定義されます.
$x_1,x_2,\dots,x_n$の多項式が対称式であるとは,$x_1,x_2,\dots,x_n$をのように入れ替えても元の多項式に等しい多項式のことをいう.
例えば,3変数$x,y,z$の対称式は
などですね.
また,$x$, $y$, $z$の基本対称式は$x+y+z$, $xy+yz+zx$, $xyz$で,やはり任意の$x$, $y$, $z$の対称式は基本対称式の和,差,積で表すことができます.
例えば,$x^2y+y^2z+z^2x+xy^2+yz^2+zx^2$は
と表せます.
一般に$n$次方程式$(t-x_1)(t-x_2)\dots(t-x_n)$を展開したときの係数に現れるもの(符号を全て$+$にしたもの)が基本対称式となります.
例えば,4変数$x,y,z,w$の基本対称式は
の係数をみて$x+y+z+w$, $xy+yz+zw+wx$, $xyz+xyw+xzw+yzw$, $xyzw$の4つとなります.
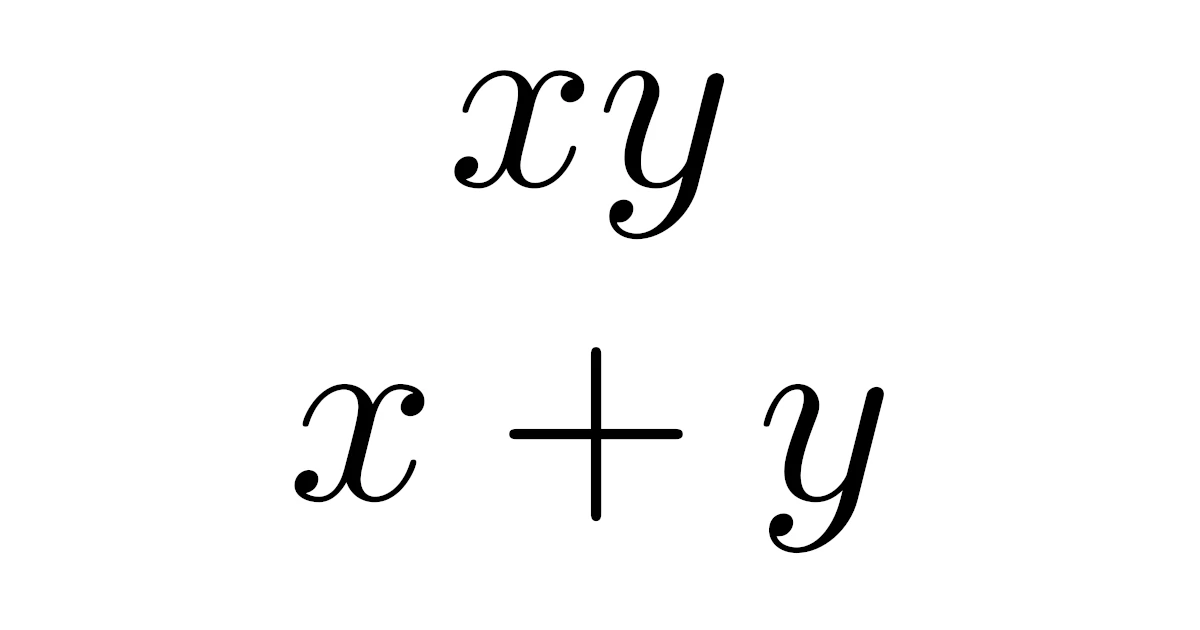
コメント