高校物理では,対象の物体を
- 質点(大きさがない物体)として考える場合
- 剛体(大きさがある物体)として考える場合
のいずれかで考えるのが普通です.
例えば,壁に立てかけた棒は大きさがある「剛体」であるとして考える必要があります.
剛体の運動を考えるときには,質点のときにも考えた力の合成に加えて,力のモーメントも重要になります.
力のモーメントと言うと難しそうに感じるかもしれませんが,ざっくりいえば小学校で学ぶ「てこの原理」の話です.
この記事では
- 質点と剛体の違い
- 力のモーメント
を順に説明します.
「剛体の運動」の一連の記事
質点と剛体の違い
たとえばボールを投げたとき,ボールには空気抵抗など様々な要因が絡まり合って運動をします.
このときのボールの運動を考えるとき,全ての要因を考えようとすると複雑になるため,「空気抵抗は考えないものとする」などと状況を簡単にして考えます.
このように,物理(に限らず科学全般)では,状況を簡略化(モデル化)して考えやすくすることをよく行います.
そのような物理での簡略化のうち「物体の大きさを考えない」と簡略化することがよくあります.
このときの「質量があり,大きさがない物体」として考えられた物体を質点といいます.
一方,たとえば壁に立てかけた棒は長さをもつものとして考えるのが妥当です.つまり,このときは物体を質点とみなす適切ではありません.
このように,「質量があり,大きさもある物体」として考えられた物体を剛体といいます.
力のモーメント
物体の回転を考える際には力のモーメントを用います.
力の作用線
力のモーメントの説明をするためには,力の作用線を理解しておきましょう.
[力の作用線] 力$\ve{F}$の「力の作用線」とは,$\ve{F}$の作用点を通り,$\ve{F}$に平行な直線のことをいう.
すなわち,力$\ve{F}$の作用点を通り,$\ve{F}$に平行な直線を「力$\ve{F}$の作用線」というわけですね.
力のモーメント
力のモーメントとは次のように定義されます.
ある物体にはたらく力$\ve{F}$と点$\mrm{A}$を考える.
このとき,点$\mrm{A}$を中心とみなして,力$\ve{F}$が物体を回転させる能力を点$\mrm{A}$周りの$\ve{F}$の力のモーメントという.
力のモーメントを考える際は
- 回転させる力はどれくらいか?
- 回転させる向きはどちらか?
のふたつが重要です.それぞれ以下で定めていきましょう.
力のモーメントの大きさ
ある物体にはたらく力$\ve{F}$と点$\mrm{A}$を考える.点$\mrm{A}$と力$\ve{F}$の作用線の距離を$\ell[\mrm{m}]$,力$\ve{F}$の大きさを$F[\mrm{N}]$とする.
このとき,点$\mrm{A}$周りの$\ve{F}$の力のモーメントの大きさを$F\ell[\mrm{Nm}]$で定める.
直感的には力のモーメントの大きさ$F\ell[\mrm{Nm}]$は「物体を回転させる強さ」のことです.
力の大きさ$F$が大きいほど物体を強く回転させることは直感に沿います.また,$\ell[\mrm{m}]$がかけられていることについては,以下のように理解できます.
例えば,レバー式のドアノブを回すとき,回転軸の近くを持ってドアノブを回すよりも,回転軸から遠くを持ってドアノブを回す方が,軽くドアノブを回すことができますね.
これは回転軸よりも遠いところに力を加えた方が,力のモーメントが大きいということに他ならないわけですね.
力のモーメントの向き
回転には時計回りと反時計回りがありますから,これについて以下のように定義します.
[力のモーメントの向き] ある物体にはたらく力$\ve{F}$と点$\mrm{A}$を考える.
このとき,点$\mrm{A}$周りの$\ve{F}$の力のモーメントの向きを
- $\ve{F}$が物体を$\mrm{A}$中心で反時計回りに回転させるとき正
- $\ve{F}$が物体を$\mrm{A}$中心で時計回りに回転させるとき負
と定める.
すなわち,
- 「反時計回り」を正
- 「時計回り」を負
と名付けただけですね.
具体例
力のモーメントは
- 力の大きさと向き
- 力の作用点
- 回転軸とみなす点
を指定して初めて考えることができることに注意して,次の問題を考えましょう.
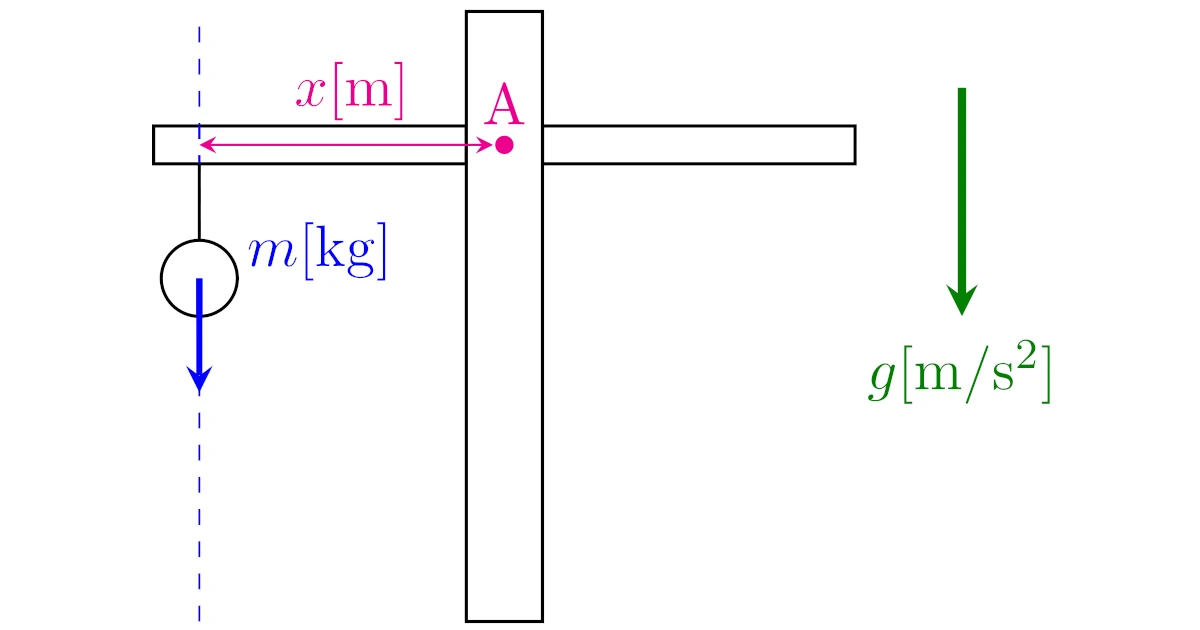
水平な天秤の左側に$m[\mrm{kg}]$の物体を軸から$x[\mrm{m}]$の位置に吊るす.天秤の回転軸を点$\mrm{A}$とするとき,$\mrm{A}$周りでの天秤にはたらく重力による力のモーメントを求めよ.
ただし,重力加速度を$g[\mrm{m/s^2}]$とする.
「力のモーメントを求めよ」と言われれば,大きさと向きを両方求めないといけないことは必ず意識しましょう.
物体にはたらく重力は鉛直下向き,大きさ$mg[\mrm{N}]$である.
また,重力の作用線は鉛直方向なので回転軸との距離は$x[\mrm{m}]$である.
よって,回転軸周りでの天秤にはたらく重力による力のモーメントは
- 大きさ:$mgx[\mrm{Nm}]$
- 向き:正方向(反時計回り)
である.
コメント