 複素数
複素数 複素数7
虚数解をもつn次方程式の頻出問題2タイプ
そもそも高校数学で複素数が現れたのは,2次方程式の実数でない解を表すためでした.この記事では,虚数解をもつn次方程式についての頻出問題を紹介します.
 複素数
複素数 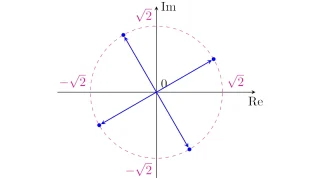 複素数
複素数 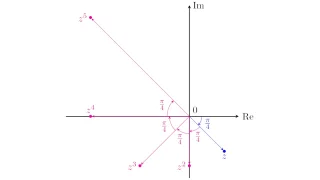 複素数
複素数 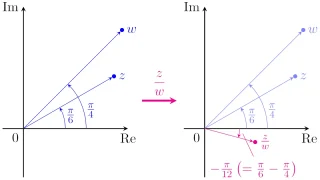 複素数
複素数 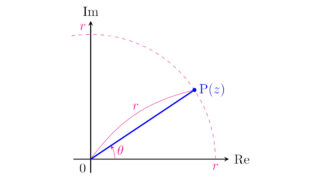 複素数
複素数 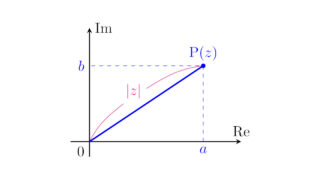 複素数
複素数 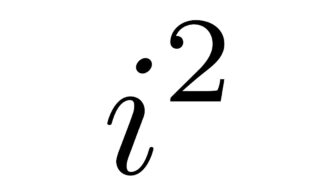 複素数
複素数 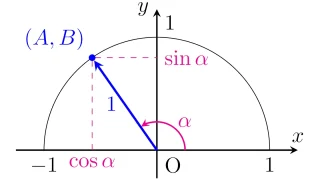 三角関数
三角関数 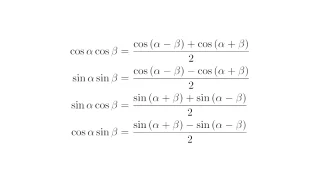 三角関数
三角関数  三角関数
三角関数