複素数の極形式の積・商｜絶対値と偏角から一瞬で計算する

複素数は絶対値$r$（原点からの距離）と偏角$\theta$の２つを用いて$r(\cos{\theta}+i\sin{\theta})$と表すことができ，この複素数の表し方を極形式というのでした．

複素数を$a+bi$（$a,b$は実数）と実部と虚部を用いて表す方法では掛け算と割り算の計算は少し面倒でしたが，実は極形式を用いると

掛け算$r(\cos{\theta}+i\sin{\theta})\cdot s(\cos{\phi}+i\sin{\phi})$
割り算$\dfrac{r(\cos{\theta}+i\sin{\theta})}{s(\cos{\phi}+i\sin{\phi})}$

が一瞬で計算できます．

この記事では

複素数の極形式の積・商の公式
複素数の極形式の積・商の証明

を順に説明します．

「複素数」の一連の記事

複素数の極形式の積・商の公式
複素数の極形式の積・商の公式の証明
1. 極形式の積
2. 極形式の商

複素数の極形式の積・商の公式

以下，極形式で表された複素数の掛け算・割り算を考えていきましょう．

極形式の積

［極形式の積］$r\geqq0$, $s\geqq0$とし，$\theta$, $\phi$を実数とする．複素数$z,w$が

$\begin{align*}&z=r(\cos{\theta}+i\sin{\theta}), \\&w=s(\cos{\phi}+i\sin{\phi})\end{align*}$

と極形式で表したとき，

$\begin{align*}zw=rs\{\cos{(\theta+\phi)}+i\sin{(\theta+\phi)}\}\end{align*}$

が成り立つ．

たとえば，複素数$z,w$が

$\begin{align*}&z=\frac{3}{2}\bra{\cos{\frac{\pi}{6}}+i\sin{\frac{\pi}{6}}}, \\&w=2\brb{\cos\bra{\frac{\pi}{4}}+i\sin\bra{\frac{\pi}{4}}}\end{align*}$

と極形式で表されたとすると，積$zw$は

$\begin{align*}zw &=\frac{3}{2}\cdot2\brb{\cos{\bra{\frac{\pi}{6}+\frac{\pi}{4}}}+i\sin{\bra{\frac{\pi}{6}+\frac{\pi}{4}}}} \\&=3\bra{\cos{\frac{5\pi}{12}}+i\sin{\frac{5\pi}{12}}},\end{align*}$

となります．

このように，

絶対値$r$, $s$の複素数をかければ，絶対値$rs$の複素数になる
偏角$\theta$, $\phi$の複素数をかければ，偏角$\theta+\phi$の複素数になる

というわけですね．

極形式の商

［極形式の商］$r\geqq0$, $s\geqq0$とし，$\theta$, $\phi$を実数とする．複素数$z,w$が

$\begin{align*}&z=r(\cos{\theta}+i\sin{\theta}), \\&w=s(\cos{\phi}+i\sin{\phi})\end{align*}$

と極形式で表したとき，

$\begin{align*}\frac{z}{w}=\frac{r}{s}\{\cos{(\theta-\phi)}+i\sin{(\theta-\phi)}\}\end{align*}$

が成り立つ．

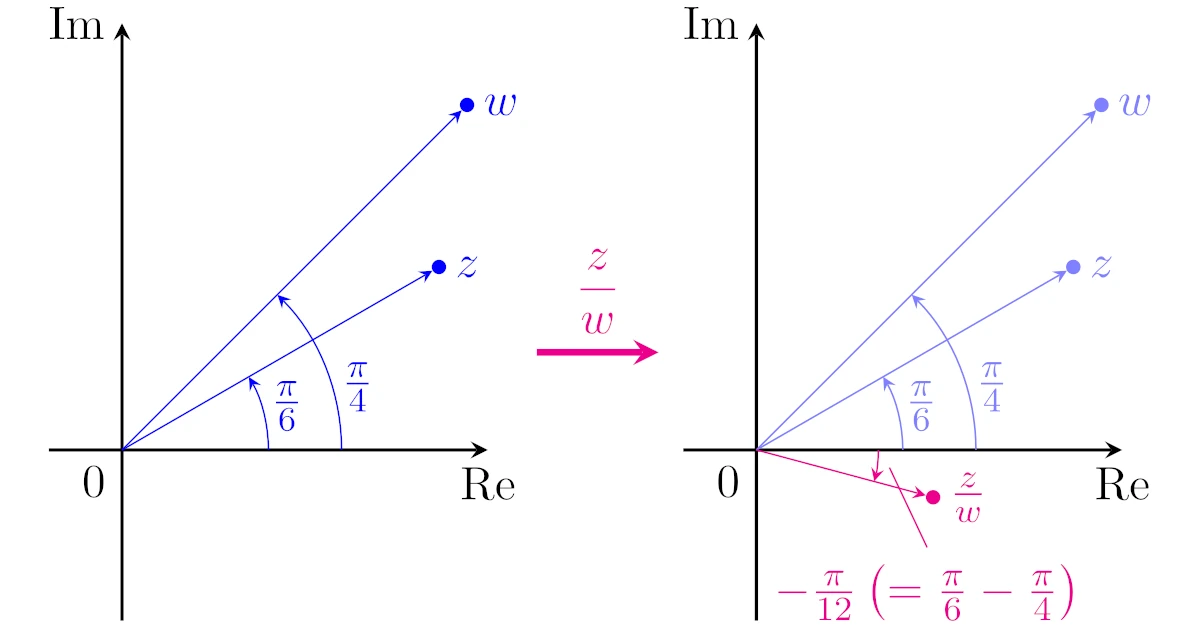
たとえば，複素数$z,w$が

$\begin{align*}&z=\frac{3}{2}\bra{\cos{\frac{\pi}{6}}+i\sin{\frac{\pi}{6}}}, \\&w=2\brb{\cos\bra{\frac{\pi}{4}}+i\sin\bra{\frac{\pi}{4}}}\end{align*}$

と極形式で表されたとすると，商$\dfrac{z}{w}$は

$\begin{align*}\frac{z}{w} &=\frac{3}{2}\cdot\frac{1}{2}\brb{\cos{\bra{\frac{\pi}{4}-\frac{\pi}{6}}}+i\sin{\bra{\frac{\pi}{4}-\frac{\pi}{6}}}} \\&=\frac{3}{4}\brb{\cos\bra{-\frac{\pi}{12}}+i\sin\bra{-\frac{\pi}{12}}}\end{align*}$

となります．

このように

絶対値$r$の複素数を，絶対値$s$の複素数で割れば，絶対値$\dfrac{r}{s}$の複素数になる
偏角$\theta$の複素数を，偏角$\phi$の複素数で割れば，偏角$\theta-\phi$の複素数になる

というわけですね．

極形式の逆数

極形式で表された複素数の商の公式について，とくに$z=1$, $w=s(\cos{\phi}+i\sin{\phi})$とすると，極形式で表された複素数の逆数をすぐに求められることも当たり前にしておきましょう．

［極形式の逆数］$s\geqq0$とし，$\phi$を実数とする．複素数$w$を

$\begin{align*}w=s(\cos{\phi}+i\sin{\phi})\end{align*}$

と極形式で表したとき，

$\begin{align*}\frac{1}{w}&=\frac{1}{s}\{\cos{(-\phi)}+i\sin{(-\phi)}\} \\&=s^{-1}(\cos{\phi}-i\sin{\phi})\end{align*}$

が成り立つ．

この逆数の公式を複素数の反転ということがあります．

複素数の極形式の積・商の公式の証明

上で紹介した極形式で表された複素数の積・商の公式を証明しましょう．

極形式の積

極形式の積の公式は三角関数の加法定理から証明することができます．

［極形式の積］$r\geqq0$, $s\geqq0$とし，$\theta$, $\phi$を実数とする．複素数$z,w$が

$\begin{align*}&z=r(\cos{\theta}+i\sin{\theta}), \\&w=s(\cos{\phi}+i\sin{\phi})\end{align*}$

と極形式で表したとき，

$\begin{align*}zw=rs\{\cos{(\theta+\phi)}+i\sin{(\theta+\phi)}\}\end{align*}$

が成り立つ．

三角関数の加法定理

$\begin{align*}&\cos{\theta}\cos{\phi}-\sin{\theta}\sin{\phi}=\cos{(\theta+\phi)}, \\&\sin{\theta}\cos{\phi}+\cos{\theta}\sin{\phi})=\sin{(\theta+\phi)}\end{align*}$

より

$\begin{align*}zw =&r(\cos{\theta}+i\sin{\theta})\cdot s(\cos{\phi}+i\sin{\phi}) \\=&rs\{(\cos{\theta}\cos{\phi}-\sin{\theta}\sin{\phi})+i(\sin{\theta}\cos{\phi}+\cos{\theta}\sin{\phi})\} \\=&rs\{\cos{(\theta+\phi)}+i\sin{(\theta+\phi)}\}\end{align*}$