複素数を極形式で表すと複素数の積や商を簡単に計算でき,複素数$z$の指数$z^n$が簡単に計算できるド・モアブルの定理を導けるのでした.
このように,複素数の極形式は指数計算に強いことは意識しておきたいポイントです.
さて,ド・モアブルの定理を用いると$z^4=1-\sqrt{3}$のような$z^n=c$型の方程式を解くことができます.
この記事では
- ド・モアブルの定理の確認
- $z^n=c$型の方程式の解き方
- 覚えておくと便利な図形的性質
を順に説明します.
「複素数」の一連の記事
ド・モアブルの定理(復習)
まずはド・モアブルの定理を復習しておきましょう.
すなわち,複素数を$n$乗すれば,
されるというわけですね.
方程式の具体例
それでは,$z^n=c$型の方程式を具体的に解きましょう.いずれも
- $z=r(\cos{\theta}+i\sin{\theta})$($r>0$, $0\leqq\theta<2\pi$)と極形式に表す
- $z$の絶対値$r$を求める
- $z$の偏角$\theta$を求める
の3ステップで解を求めることができます.
例1($z^6=1$)
$z$の方程式$z^6=1$を解け.
極形式で$z=r(\cos{\theta}+i\sin{\theta})$($r>0$, $0\leqq\theta<2\pi$)と表すと,ド・モアブルの定理より
となり,両辺で絶対値を考えると$r^6=1$なので$r=1$となります.
と偏角が求まります.ただし,$0\leqq\theta<2\pi$から$0\leqq6\theta<12\pi$が成り立つことに注意.
よって,方程式$z^6=1$の解は
- $1(\cos{0}+i\sin{0})=1$
- $1\Bigl(\cos{\dfrac{\pi}{3}}+i\sin{\dfrac{\pi}{3}}\Bigr)=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i$
- $1\Bigl(\cos{\dfrac{2\pi}{3}}+i\sin{\dfrac{2\pi}{3}}\Bigr)=-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i$
- $1(\cos{\pi}+i\sin{\pi})=-1$
- $1\Bigl(\cos{\dfrac{4\pi}{3}}+i\sin{\dfrac{4\pi}{3}}\Bigr)=-\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i$
- $1\Bigl(\cos{\dfrac{5\pi}{3}}+i\sin{\dfrac{5\pi}{3}}\Bigr)=\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i$
となります.
なお,解を複素平面上に図示すると下図のようになります.
例2($z^3=-2$)
$z$の方程式$z^3=-2$を解け.
極形式で$z=r(\cos{\theta}+i\sin{\theta})$($r>0$, $0\leqq\theta<2\pi$)と表すと,ド・モアブルの定理より
となり,両辺で絶対値を考えると$r^3=2$なので$r=\sqrt[3]{2}$となります.
よって,$r=\sqrt[3]{2}$を代入して,実部と虚部を比較して
と偏角が求まります.ただし,$0\leqq\theta<2\pi$から$0\leqq3\theta<6\pi$が成り立つことに注意.
よって,方程式$z^3=-2$の解は
- $\sqrt[3]{2}\Bigl(\cos{\dfrac{\pi}{3}}+i\sin{\dfrac{\pi}{3}}\Bigr)=\sqrt[3]{2}\Bigl(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i\Bigr)$
- $\sqrt[3]{2}(\cos{\pi}+i\sin{\pi})=-\sqrt[3]{2}$
- $\sqrt[3]{2}\Bigl(\cos{\dfrac{5\pi}{3}}+i\sin{\dfrac{5\pi}{3}}\Bigr)=\sqrt[3]{2}\Bigl(\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i\Bigr)$
となります.
なお,解を複素平面上に図示すると下図のようになります.
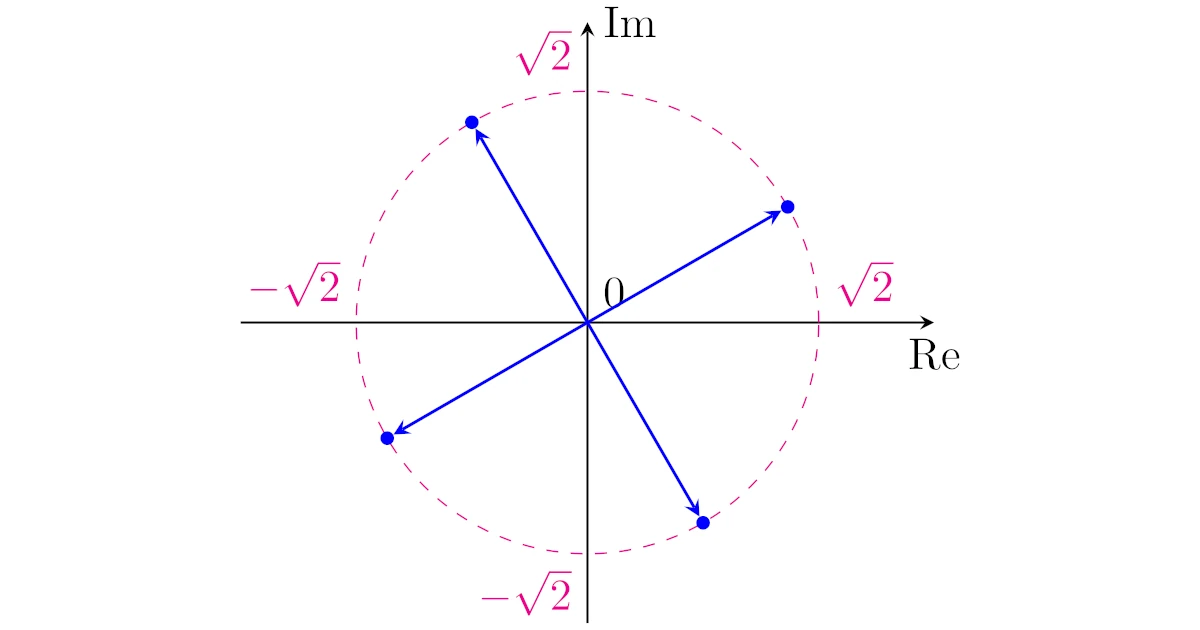
例3($z^4=-1+\sqrt{3}$)
$z$の方程式$z^4=-1+\sqrt{3}i$を解け.
極形式で$z=r(\cos{\theta}+i\sin{\theta})$($r>0$, $0\leqq\theta<2\pi$)と表すと,ド・モアブルの定理より
となり,両辺で絶対値を考えると$r^4=\sqrt{(-1)^2+(\sqrt{3})^2}$なので$r=\sqrt{2}$となります.
よって,$r=\sqrt{2}$を代入して,実部と虚部を比較して
と偏角が求まります.ただし,$0\leqq\theta<2\pi$から$0\leqq4\theta<8\pi$が成り立つことに注意.
よって,方程式$z^4=-1+\sqrt{3}i$の解は
- $\sqrt{2}\Bigl(\cos{\dfrac{\pi}{6}}+i\sin{\dfrac{\pi}{6}}\Bigr)=\sqrt{2}\Bigl(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\Bigr)$
- $\sqrt{2}\Bigl(\cos{\dfrac{2\pi}{3}}+i\sin{\dfrac{2\pi}{3}}\Bigr)=\sqrt{2}\Bigl(-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i\Bigr)$
- $\sqrt{2}\Bigl(\cos{\dfrac{7\pi}{6}}+i\sin{\dfrac{7\pi}{6}}\Bigr)=\sqrt{2}\Bigl(-\dfrac{\sqrt{3}}{2}-\dfrac{1}{2}i\Bigr)$
- $\sqrt{2}\Bigl(\cos{\dfrac{5\pi}{3}}+i\sin{\dfrac{5\pi}{3}}\Bigr)=\sqrt{2}\Bigl(\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i\Bigr)$
となります.
なお,解を複素平面上に図示すると下図のようになります.
覚えておくと便利な図形的性質
いまみた3つの例の解を複素平面上に図示すると,いずれの場合も
- 原点中心の円周上に
- 等間隔に
並んでいることが分かります.実は一般に以下が成り立ちます.
$c$を複素数,$n$を正の整数とする.$z$の方程式$z^n=c$の解は複素平面上で,原点中心,半径$\sqrt[n]{|c|}$の円周上に等間隔に存在する.
これを知っていれば1つ解から他の解もすぐに求めることができますし,間違っていればすぐに気付くことができますね.
コメント