導関数から極大値，極小値を求める基本的な方法

実は３次以上の多項式$f(x)$で最大値・最小値を求めたいとき，最大値・最小値の候補である

極大値
極小値

というものを調べることが重要です．

２次関数でもそうでしたが，関数$f(x)$の最大値・最小値を考えるためには$y=f(x)$のグラフを描く（増減を調べる）ことが大切なのでした．

３次以上の多項式$f(x)$に対しても，前回の記事で説明した$y=f(x)$のグラフを描く要領で考えれば，$f(x)$の極大値・極小値を求めることができます．

この記事では

極大値・極小値とは何か？
導関数と極値の関係
極値の具体例

を順に説明します．

「微分法」の一連の記事

極大値と極小値
導関数と極値の関係
1. 極値の候補を求める定理
2. 定理の注意点
具体例

極大値と極小値

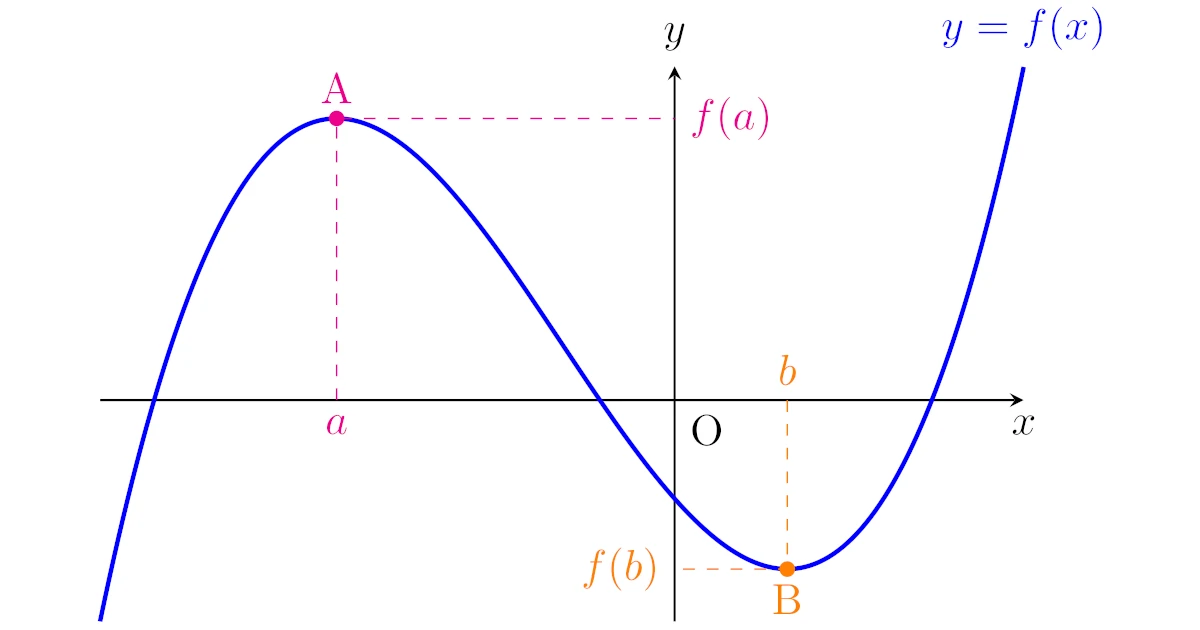
さっそく関数の極大値・極小値を定義しましょう．

関数$f(x)$と実数$a$, $b$に対して，２点$\mrm{A}(a,f(a))$, $\mrm{B}(b,f(b))$を考える．このとき，

$x=a$の近くにおいて，$f(x)$が$x=a$で最大値をとるとき，$f(a)$を$f(x)$の極大値
$x=b$の近くにおいて，$f(x)$が$x=b$で最小値をとるとき，$f(b)$を$f(x)$の極小値

という．また，極大値と極小値を併せて極値といい，$x=a$を極大点，$x=b$を極小点という．

要するに

ひとつひとつの「山の頂上」の標高を極大値
ひとつひとつの「谷の底」の標高を極小値

というわけですね．

よって，極大点・極小点はいくつも存在し得ますね．

導関数と極値の関係

微分可能な関数の極値を求めるためには，導関数を用いる方法が基本的です．

極値の候補を求める定理

結論から書けば，次の定理が成り立ちます．

微分可能な関数$f(x)$が$x=a$で極値をもつなら$f'(a)=0$を満たす．このとき，さらに$x=a$の前後で

$f'(x)>0$から$f'(x)<0$となるとき，$f(a)$は極大値である
$f'(x)<0$から$f'(x)>0$となるとき，$f(a)$は極小値である

つまり，微分可能な$f(x)$に対して，導関数$f'(x)$から$f(x)$の極値の候補を見つけることができるわけですね．

以下のグラフからもみてとれるように，微分可能な$f(x)$が$x=a$で極値をとるとき，点$(a,f(a))$の接線は平らになりますね．つまり，接線の傾きが$0$になっています．

さらに，

極大値となるところでは関数が増加↗︎から減少↘︎に移る
極小値となるところでは関数が減少↘︎から減少↗︎に移る

ということがみてとれますね．

定理の注意点

先ほどの定理は「$f(x)$が$x=a$で極値をもつ → $f'(a)=0$をみたす」という主張であり，この逆は正しくないことがあります．

関数$f(x)$と実数$a$に対して，$f'(a)=0$であっても$f(x)$が$x=a$に極値をもつとは限らない．

ですから，方程式$f'(x)=0$を解いて解が$x=a$と得られても，すぐに「$f(a)$は極値だ！」とはいえないわけですね．

例えば，$f(x)=x^3$に対しては$f'(x)=3x^2$となるので$f'(0)=0$です．

しかし，$f'(x)=3x^2$は常に$0$以上となるため，減少に転ずることがありません．よって，$y=f(x)$のグラフは下図のようになっており，$x=0$で極値をもちませんね．

このように，$f'(x)$が$0$になってもその前後で正負が変化しない場合には極値とならないわけですね．

具体例

それでは具体例を考えましょう．

例１

$f(x)=\dfrac{1}{4}\bra{x^3+3x^2-9x-7}$の極値を求めよ．また，それらの極値は最大値または最小値をとるか？

$f(x)=\dfrac{1}{4}(x^3+3x^2-9x-7)$の導関数は

$\begin{align*} f'(x) =&\frac{1}{4}(3x^2+6x-9) \\=&\frac{3}{4}(x+3)(x-1) \end{align*}$

なので，方程式$f'(x)=0$は$x=-3,1$と解けます．また，計算して$f(-3)=5$, $f(1)=-3$だから，$f(x)$の増減表は

$\begin{align*} \begin{array}{c||c|c|c|c|c} x & \dots & -3 & \dots & 1 & \dots \\ \hline f'(x) & + & 0 & - & 0 & + \\ \hline f(x) &\nearrow & 5 & \searrow& -3 & \nearrow \end{array} \end{align*}$

となります．よって，増減表から$f(x)$は

$x=-3$で極大値$5$
$x=1$で極小値$-3$

をとることが分かります．

これらの極値はどちらも最大値・最小値ではありませんね．

例２

同じ関数の式で定義域を狭めるとどうなるでしょうか？

$f(x)=\dfrac{1}{4}\bra{x^3+3x^2-9x-7}$ ($-4\leqq x$)の極値を求めよ．また，それらの極値は最大値または最小値をとるか？

例１の関数の定義域が$-4\leqq x$に制限されただけだから，$f(x)$の増減表は同様に

$\begin{align*} \begin{array}{c||c|c|c|c|c|c} x & -4 & \dots & -3 & \dots & 1 & \dots \\ \hline f'(x) & + & + & 0 & - & 0 & + \\ \hline f(x) & \frac{13}{4} & \nearrow & 5 & \searrow& -3 & \nearrow \end{array} \end{align*}$

となります．よって，増減表から$f(x)$は

$x=-3$で極大値$5$
$x=1$で極小値$-3$

をとることが分かります．

これらの極値のうち，極小値$-3$ ($x=1$)は最小値ですが，極大値$5$ ($x=-3$)は最大値ではありませんね．

例３

微分可能ではないような場合にも極値といいます．

$f(x)=|x+1|-3$の極値を求めよ．

$f(x)=|x+1|-3$に対して，$y=f(x)$のグラフは$y=|x|$のグラフを

$x$軸方向にちょうど$-1$
$y$軸方向にちょうど$-3$

平行移動したグラフなので，下図のようになります．

よって，$x=0$で極小値$-3$をとり，極大値は存在しませんね．

さらに，この極小値は最小値でもあります．

このように尖っている（微分不可能な）場合でも

周囲より高くなっていれば極大値
周囲より低くなっていれば極小値

ということに注意しましょう．

微分法５
導関数から極大値，極小値を求める方法

極大値と極小値

導関数と極値の関係

極値の候補を求める定理

定理の注意点

具体例

例１

例２

例３

コメント