2次式の因数分解には基本公式$x^2+(a+b)x+ab=(x+a)(x+b)$がありましたが,この公式は直接的には$x^2$の係数が1の2次式にしか使えません.
例えば,
- 2次式$2x^2+7x+3$を因数分解せよ.
- 2次式$6x^2+7x-3$を因数分解せよ.
といった$x^2$の係数が1でない2次式の因数分解をしたいときには,たすきがけ因数分解の公式が使えることがあります.
この記事では
- たすきがけ因数分解の公式と具体例
- たすきがけ因数分解の公式を使わない場合
を順に解説します.
「多項式」の一連の記事
たすきがけ因数分解の公式と具体例
まずはたすきがけ因数分解の公式を説明し,具体例を見てみましょう.
たすきがけ因数分解の公式の考え方
次の公式をたすきがけ因数分解の公式と呼びます.
実数$x$, $a$, $b$, $c$, $d$に対して,等式
\begin{align*}acx^2+(bc+ad)x+bd=(ax+b)(cx+d)\end{align*}
が成り立つ.
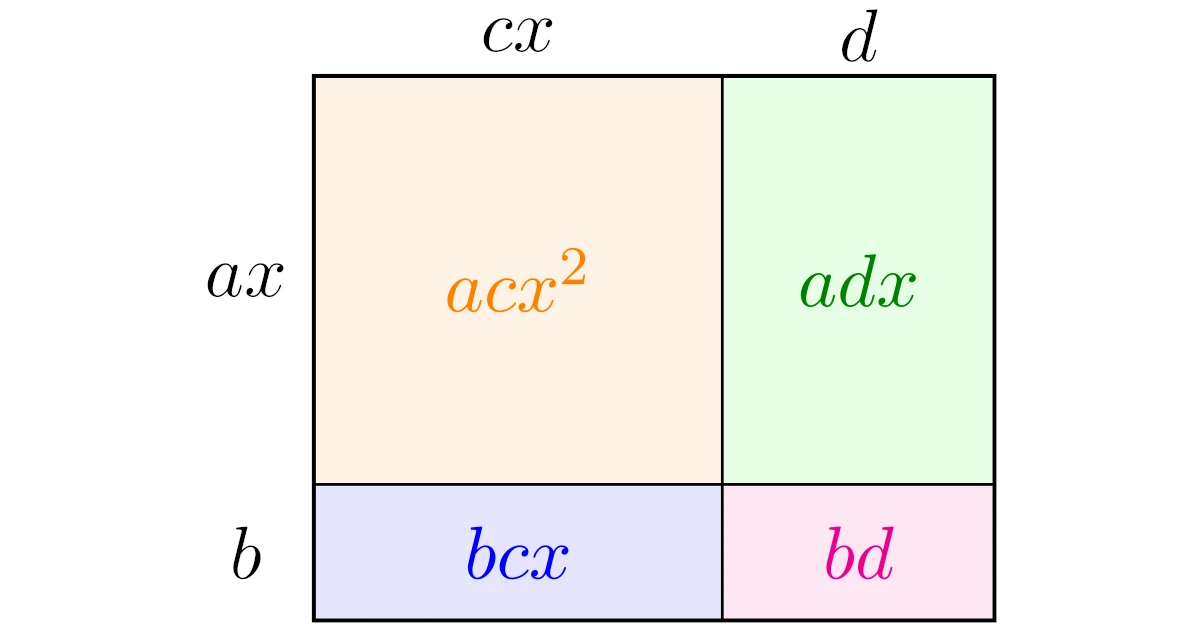
2次式の因数分解の基本公式$x^2+(a+b)x+ab=(x+a)(x+b)$と同様に,$ax$, $b$, $cx$, $d$が全て正の場合は次のように図形的に理解することもできますね.
ただ注意したいことは,たすきがけ因数分解の公式は使い方が大切な公式で,ただ暗記したとしても使えるようにはならないという点です.以下の具体例で使い方を見ていきましょう.
具体例1(x^2+7x+3$の因数分解)
2次式$2x^2+7x+3$を因数分解せよ.
2つのステップに分けて因数分解しましょう.
ステップ1(2次の係数と定数の候補)
まず$2x^2+7x+3$の2次の係数が2であることから
\begin{align*}(x+\underline{\qquad})(2x+\underline{\qquad})\end{align*}
の形に因数分解できることが期待できます.
さらに,定数項が3であることから,因数分解の候補として
- $(x+3)(2x+1)$
- $(x+1)(2x+3)$
- $(x-3)(2x-1)$
- $(x-1)(2x-3)$
が挙げられますね.
ステップ2(満たすものを見つける)
これらを実際に展開すると
- $2x^2{\color{blue}+7}x+3$
- $2x^2{\color{blue}+5}x+3$
- $2x^2{\color{blue}-7}x+3$
- $2x^2{\color{blue}-5}x+3$
となっていますから,これらのうち$2x^2+7x+3$の因数分解になっているのは$(x+3)(2x+1)$ですね.よって,
\begin{align*}2x^2+7x+3=(x+3)(2x+1)\end{align*}
と因数分解できます.
このように,たすきがけ因数分解の公式は覚えていることが大切なのではなく,考え方が大切な公式です(むしろ公式を暗記して使おうとする方が無理ですね).
慣れれば1次の係数の$7$が$6+1=3\cdot2+1\cdot1$に見えて,$(x+3)(2x+1)$と数秒で因数分解できるようになります.
具体例2(x^2+7x-3$の因数分解)
2次式$6x^2+7x-3$を因数分解せよ.
この問題もやはり2つのステップに分けて因数分解しましょう.
ステップ1(2次の係数と定数の候補)
$6x^2+7x-3$の2次の係数が$6$であることから
\begin{align*}(x+\underline{\qquad})(6x+\underline{\qquad})\end{align*}
または
\begin{align*}(2x+\underline{\qquad})(3x+\underline{\qquad})\end{align*}
の形に因数分解できることが期待できます.
さらに,定数項が$-3$であることから,因数分解の候補として
- $(x+1)(6x-3)$
- $(x-1)(6x+3)$
- $(x+3)(6x-1)$
- $(x-3)(6x+1)$
- $(2x+1)(3x-3)$
- $(2x-1)(3x+3)$
- $(2x+3)(3x-1)$
- $(2x-3)(3x+1)$
が挙げられますね.
ステップ2(満たすものを見つける)
これらを実際に展開すると
- $6x^2{\color{blue}+3}x-3$
- $6x^2{\color{blue}-3}x-3$
- $6x^2{\color{blue}+17}x-3$
- $6x^2{\color{blue}-17}x-3$
- $6x^2{\color{blue}-3}x-3$
- $6x^2{\color{blue}+3}x-3$
- $6x^2{\color{blue}+7}x-3$
- $6x^2{\color{blue}-7}x-3$
ですから,このうち$6x^2+7x-3$の因数分解になっているのは$(2x+3)(3x-1)$ですね.よって,
\begin{align*}6x^2+7x-3=(2x+3)(3x-1)\end{align*}
と因数分解されることが分かります.
慣れればこの程度の問題なら1次の係数の$7$が$9-2=3\cdot3-1\cdot2$に見えて,$(2x+3)(3x-1)$と数秒で因数分解できるようになります.
たすきがけ因数分解の公式を使わない場合
2次の係数が1でない場合でも,たすきがけ因数分解の公式を使うとは限りません.
共通因数でくくるタイプ
次の問題は$x^2$の係数が1でない場合の2次式の因数分解ですが,たすきがけ因数分解の公式は使いません.
2次式$3x^2-6x+3$を因数分解せよ.
因数分解するときに一番最初に考えるべきことは「共通因数でくくる」です.いまの問題の多項式は共通因数3でくくれますから,次のように因数分解されますね.
3でくくって$(x-a)^2=x^2-2ax+a^2$の公式を用いると
\begin{align*}3x^2-6x+3
&=3(x^2-2x+1)
\\&=3(x-1)^2\end{align*}
と因数分解できる.
たすきがけ因数分解を用いても因数分解できますが,面倒なので共通因数でくくれるかどうかには常にアンテナを張っておきたいところです.
そもそも因数分解が難しいタイプ
例えば,2次式$2x^2+x-2$は実際に因数分解すると
\begin{align*}2x^2+x-2=\bra{2x+\frac{1+\sqrt{17}}{2}}\bra{x+\frac{1-\sqrt{17}}{4}}\end{align*}
となります.右辺を展開すれば左辺になることは分かりますが,左辺から右辺を思い付くのは至難の業ですね.このような因数分解の問題では,別の方法を用いることになります.
このような場合にどうすれば因数分解できるかについては,のちの2次方程式の解の公式の記事で説明しています.
コメント