下図の$\tri{ABC}$を考えたとき,中学校で学ぶ三平方の定理を用いると,斜辺$\mrm{AC}$の長さは
と計算できますね.
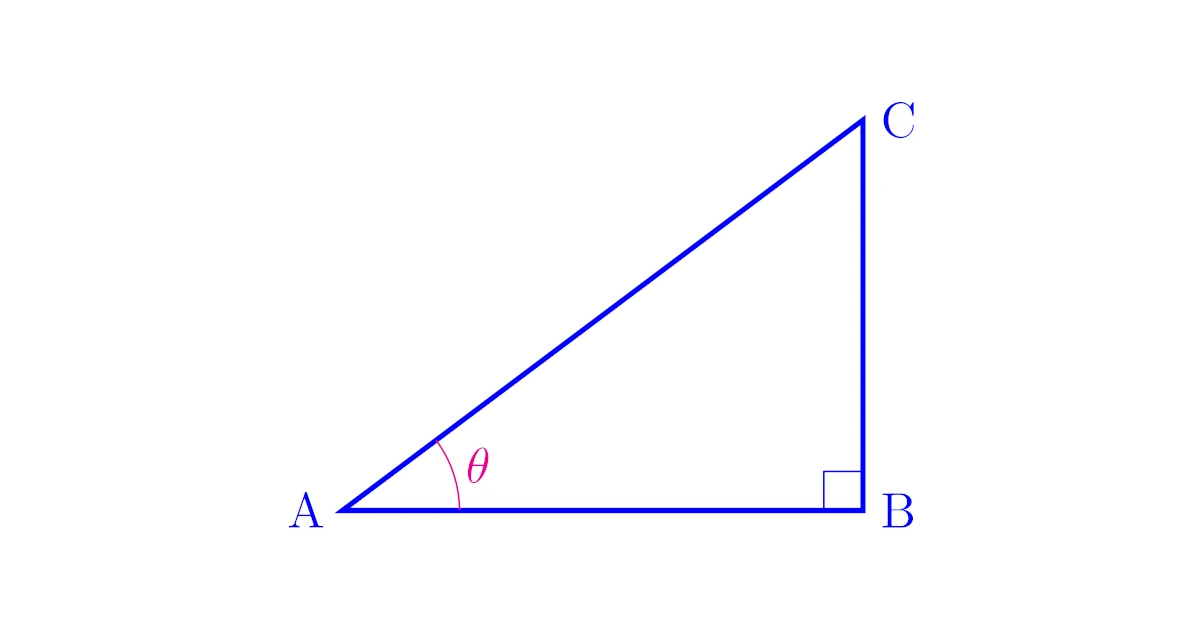
このように,直角三角形の2辺の長さが与えられている場合には三平方の定理から残り1辺の長さが求められますが,下図の$\tri{ABC}$の辺$\mrm{BC}$の長さはどのようにすれば表せるでしょうか?
このような三角形$\mrm{ABC}$はひとつに定まるので,辺$\mrm{BC}$の長さも定まっていますが,三平方の定理だけから長さを求めるのは難しそうですね.
しかし,実は三角比
というものを用いると,いまのような表すことが難しい辺の長さも表すことができるようになります.
この記事では
- 三角比とは何か?
- 三角比はどのように便利か?
- 有名角の三角比の値
を順に説明します.
「三角比」の一連の記事
三角比とは何か?
まずは三角比の定義を説明してから,三角比の便利さを説明します.
三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$の考え方
$\ang{B}=90^{\circ}$の$\tri{ABC}$と,$\ang{B’}=90^{\circ}$の$\tri{A’B’C’}$を考えます.
このとき,もし$\ang{A}=\ang{A’}$であれば,この2つの直角三角形は2つの角がそれぞれ等しいので相似であることが分かります.
よって,相似$\tri{ABC}\sim\tri{A’B’C’}$により,$\mrm{AB}:\mrm{BC}:\mrm{CA}=\mrm{A’B’}:\mrm{B’C’}:\mrm{C’A’}$が成り立つので,
が成り立ちます.
つまり,$\ang{B}=\ang{90^{\circ}}$の直角三角形で$\ang{A}$の大きささえ決めてしまえば,三角形の大きさによらず辺の比$\dfrac{\mrm{AB}}{\mrm{AC}}$, $\dfrac{\mrm{BC}}{\mrm{AC}}$, $\dfrac{\mrm{CB}}{\mrm{AB}}$の値が一定ということになります.
そこで,「$\ang{A}$を決めればこれら3つの辺の比が決まるから,この3つの辺の比に名前をつけよう」ということで,以下のように三角比を定義します.
$\ang{B}=90^{\circ}$の直角三角形$\tri{ABC}$に対して,$\theta=\ang{A}$とする.
このとき,$\cos{\theta}$, $\sin{\theta}$, $\tan{\theta}$を
と定める.また,$\cos$を余弦,$\sin$を正弦,$\tan$を正接という.
どの辺の比がどの三角比になるのかは,ルール(定義)なので覚えてください.
三角比が便利な理由
冒頭でも考えた$\ang{A}=25^\circ$, $\ang{B}=90^\circ$, $\mrm{AB}=3$の直角三角形を考えましょう.
このとき,中学数学までの知識では辺$\mrm{AB}$や辺$\mrm{BC}$の長さを表そうとしても,どうにも難しいです.
しかし,三角比を使えば
と表すことができます.
このように三角比を用いることで新たに辺の長さを表現できるようになることが,三角比が便利な大きな理由です.
「$\sin{25^\circ}$や$\cos{25^\circ}$の値が分からないから分かった気にならない」という意見もときどき頂きますが,「とりあえず表現できるようになった」ということだけでもかなりの前進です.
具体的な三角比の値
$30^\circ$, $45\circ$, $60^\circ$に関する三角比は三平方の定理から簡単に求まるので,
- $\sin{30^\circ}$, $\cos{30^\circ}$, $\tan{30^\circ}$
- $\sin{45^\circ}$, $\cos{45^\circ}$, $\tan{45^\circ}$
- $\sin{60^\circ}$, $\cos{60^\circ}$, $\tan{60^\circ}$
は有名角の三角比と呼ばれることがあります.
${30^\circ}$の三角比
$\cos{30^\circ}$, $\sin{30^\circ}$, $\tan{30^\circ}$を以下の図で考えましょう.
$\tri{ABC}$は以下の正三角形$\tri{ACC’}$を半分にした三角形ですね.
よって,$\mrm{BC}:\mrm{CA}=\dfrac{1}{2}\mrm{CC’}:\mrm{CA}=1:2$ですから,三平方の定理より$\mrm{AB}:\mrm{BC}:\mrm{CA}=\sqrt{3}:1:2$となり,
が分かります.
${45^\circ}$の三角比
$\cos{45^\circ}$, $\sin{45^\circ}$, $\tan{45^\circ}$を以下の図で考えましょう.
$\tri{ABC}$は$\mrm{AB}=\mrm{BC}$, $\ang{B}=90^{\circ}$の直角二等辺三角形なので,三平方の定理と併せて$\mrm{AB}:\mrm{BC}:\mrm{CA}=1:1:\sqrt{2}$となり,
が分かります.
${60^\circ}$の三角比
$\cos{60^\circ}$, $\sin{60^\circ}$, $\tan{60^\circ}$を以下の図で考えましょう.
これは$30^\circ$のときと相似なので,辺の比は等しく$\mrm{AB}:\mrm{BC}:\mrm{CA}=1:\sqrt{3}:2$となり,
が分かります.
有名角の三角比のまとめ
以上をまとめると
| $\theta$ | $30^\circ$ | $45^\circ$ | $60^\circ$ |
|---|---|---|---|
| $\cos{\theta}$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{\sqrt{2}}\biggl(=\dfrac{\sqrt{2}}{2}\biggr)$ | $\dfrac{1}{2}$ |
| $\sin{\theta}$ | $\dfrac{1}{2}$ | $\dfrac{1}{\sqrt{2}}\biggl(=\dfrac{\sqrt{2}}{2}\biggr)$ | $\dfrac{\sqrt{3}}{2}$ |
| $\tan{\theta}$ | $\dfrac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ |
となりますね.
覚え方
邪道な覚え方ですが,$\sin{\theta}$は$\theta$が$30^{\circ}$→$45^{\circ}$→$60^{\circ}$となるとき
とたまたま分子の$\sqrt{\quad}$の中身が$1$→$2$→$3$と増えていきます.これを知っていれば覚えやすいかと思います.
$\cos{\theta}$はこの逆で$\theta$が$30^{\circ}$→$45^{\circ}$→$60^{\circ}$となるとき
となっていますね.
$\sin{45^\circ}$, $\cos{45^\circ}$の値
$\sin{45^\circ}$, $\cos{45^\circ}$の値は
のどちらで表されることも多いです.
どちらも同じ値だという感覚は持っておきたいところです.
コメント