$\ang{A}=\theta$, $\ang{B}=90^{\circ}$の$\tri{ABC}$に対して,辺の比$\dfrac{\mrm{AB}}{\mrm{AC}}$, $\dfrac{\mrm{BC}}{\mrm{AC}}$, $\dfrac{\mrm{CB}}{\mrm{AB}}$に
と名前をつけたものが三角比なのでした.
実は三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$はそれぞれ独立したものではなく,互いに関係があります.
この記事では
- 三角比$\sin$, $\cos$, $\tan$の相互関係
- 三角比$\sin$, $\cos$, $\tan$の相互関係の証明
を順に解説します.
「三角比」の一連の記事
三角比$\sin$, $\cos$, $\tan$の相互関係
まずはひとつ問題を考えてから三角比の相互関係を説明します.
$\sin{\theta}$から$\cos{\theta}$, $\tan{\theta}$を求める問題
三角比の定義をもとに次の問題を考えてみましょう.
$\sin{\theta}=\dfrac{1}{3}$($0<\theta<90^\circ$)が成り立つとき,$\cos{\theta}$, $\tan{\theta}$を求めよ.
この問題で大切なことは,$\sin{\theta}$を決めればひとつの内角が$\theta$の直角三角形の辺の比が決まるということです.
そのため,$\cos{\theta}$も$\tan{\theta}$もひとつに決まるはずですから,次のような解答が考えられますね.
$\theta$は$\sin{\theta}=\dfrac{1}{3}$を満たすから下図のような直角三角形が描ける.
このとき,三平方の定理から
なので,
である.
三角比$\sin$, $\cos$, $\tan$の間に成り立つ関係式
$\sin{\theta}$が決まれば$\cos{\theta}$, $\tan{\theta}$も決まるということは,三角比$\sin$, $\cos$, $\tan$たちの間にはなんらかの関係があるということですね.
実際,これらの間には次の等式が成り立ちます.
ひとつの内角の大きさが$\theta$の直角三角形について,4つの等式
- $\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$
- $\cos^{2}{\theta}+\sin^{2}{\theta}=1$
- $1+\tan^{2}{\theta}=\dfrac{1}{\cos^{2}{\theta}}$
- $1+\dfrac{1}{\tan^{2}{\theta}}=\dfrac{1}{\sin^{2}{\theta}}$
が成り立つ.
教科書によって4つ目の関係式が載っていないこともあります.
それぞれを
- $\sin{\theta},\cos{\theta},\tan{\theta}$の関係式
- $\sin{\theta},\cos{\theta}$の関係式
- $\cos{\theta},\tan{\theta}$の関係式
- $\sin{\theta},\tan{\theta}$の関係式
と捉えると,それぞれどういう等式か分かりやすいですね.
公式による解答
これらの公式を用いて,先ほどの問題をもう一度解いてみましょう.
(再掲)$\sin{\theta}=\dfrac{1}{3}$($0<\theta<90^\circ$)が成り立つとき,$\cos{\theta}$, $\tan{\theta}$を求めよ.
$\sin{\theta}$と$\cos{\theta}$の関係式$\cos^{2}{\theta}+\sin^{2}{\theta}=1$より
が成り立つ.$\cos{\theta}>0$だから$\cos{\theta}=\dfrac{2\sqrt{2}}{3}$である.
また,$\sin{\theta},\cos{\theta},\tan{\theta}$の関係式$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$より
を得る.
公式を使えば図を描かなくても計算だけで求まるのは嬉しいですね.
三角比$\sin$, $\cos$, $\tan$の相互関係の証明
三角比の相互関係を従って証明しましょう.
(再掲)ひとつの内角の大きさが$\theta$の直角三角形について,4つの等式
- $\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$
- $\cos^{2}{\theta}+\sin^{2}{\theta}=1$
- $1+\tan^{2}{\theta}=\dfrac{1}{\cos^{2}{\theta}}$
- $1+\dfrac{1}{\tan^{2}{\theta}}=\dfrac{1}{\sin^{2}{\theta}}$
が成り立つ.
$\ang{A}=\theta$, $\ang{B}=90^{\circ}$の直角三角形$\tri{ABC}$に対して,
である.
$\sin$, $\cos$, $\tan$の関係式の証明
$\sin{\theta},\cos{\theta},\tan{\theta}$の定義より
だから両辺を$\cos{\theta}$で割って,$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$を得る.
$\sin$, $\cos$の関係式の証明
$\sin{\theta},\cos{\theta}$の定義と三平方の定理$\mrm{AB}^2+\mrm{BC}^2=\mrm{CA}^2$を用いると
が成り立つ.
$\cos$, $\tan$の関係式の証明
いま得られた$\cos^2{\theta}+\sin^2{\theta}=1$の両辺を$\cos^2{\theta}$で割って
が成り立つ.左辺の第2項目で$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$を用いて$1+\tan^2{\theta}=\dfrac{1}{\cos^2{\theta}}$を得る.
$\sin$, $\tan$の関係式の証明
同様に$\cos^2{\theta}+\sin^2{\theta}=1$の両辺を$\sin^2{\theta}$で割って
が成り立つ.左辺の第2項目で$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$(の逆数)を用いて$1+\dfrac{1}{\tan^2{\theta}}=\dfrac{1}{\cos^2{\theta}}$を得る.
証明の補足
照明の流れとしては,定義から
- $\sin$, $\cos$, $\tan$の関係式$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$
- $\sin$, $\cos$の関係式$\cos^2{\theta}+\sin^2{\theta}=1$
を示し,これらから残る2つの関係式
- $\cos$, $\tan$の関係式$1+\tan^2{\theta}=\dfrac{1}{\cos^2{\theta}}$
- $\sin$, $\tan$の関係式$1+\dfrac{1}{\tan^2{\theta}}=\dfrac{1}{\cos^2{\theta}}$
を証明したわけですね.(3)と(4)の公式自体は少し複雑に見えるかもしれませんが,いまの証明が分かっていれば忘れても(1)と(2)からすぐに導けますね.
3つ目の$\cos$, $\tan$の関係式,4つ目の$\sin$, $\tan$の関係式も定義に従って証明することもできます.
なお,$\sin{\theta},\cos{\theta},\tan{\theta}$の関係式$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$は分母を払った
の形でも覚えておくと便利なこともよくあります.
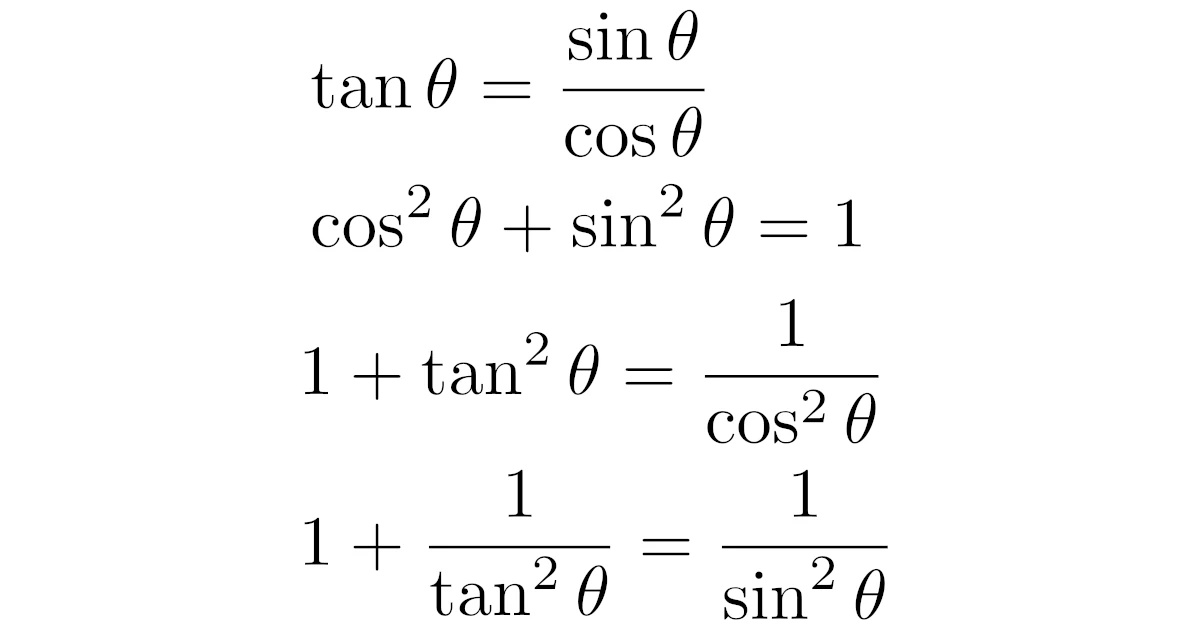
コメント