ベクトルの三角形の面積公式｜ベクトルの内積の便利な使い方

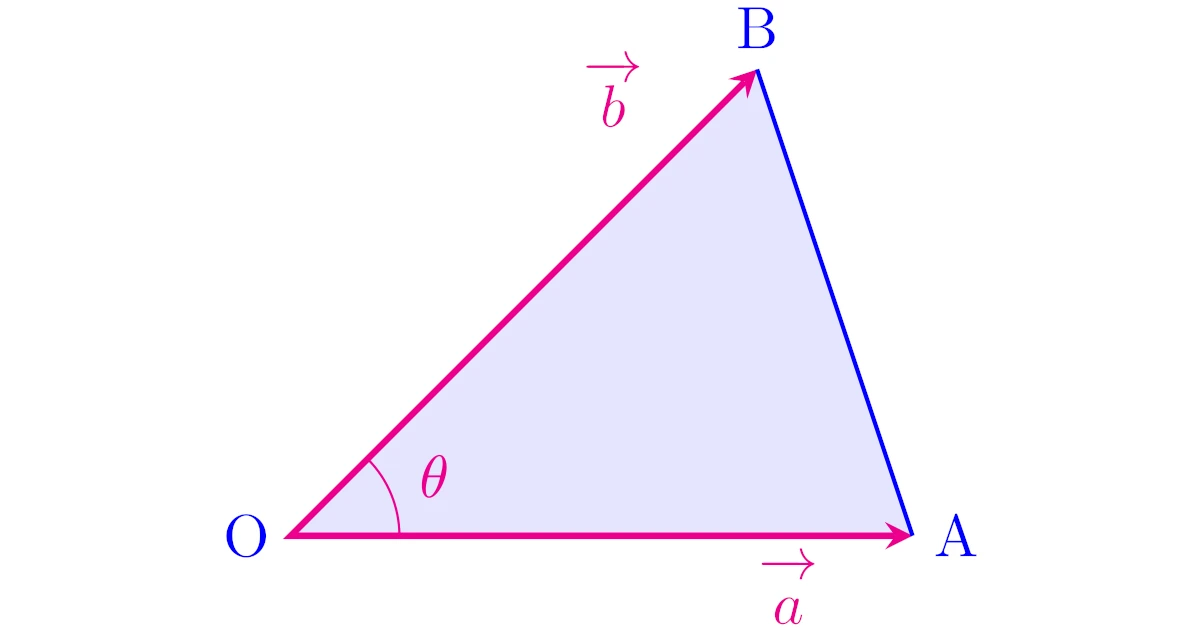
三角形$\mrm{OAB}$の面積$S$は，$\theta=\ang{O}$とすると

$\begin{align*}S=\frac{1}{2}\mrm{OA}\cdot\mrm{OB}\sin{\theta}\end{align*}$

と求められることを三角比の分野で学びました．

また，$\theta$は２つのベクトル$\Ve{OA}$, $\Ve{OB}$のなす角なので，内積の定義より

$\begin{align*}\Ve{OA}\cdot\Ve{OB}=|\Ve{OA}||\Ve{OB}|\cos{\theta}\end{align*}$

ですね．

よって，これらの式から$\cos{\theta}$と$\sin{\theta}$を消去すれば，三角形$\mrm{OAB}$の面積$S$を内積$\Ve{OA}\cdot\Ve{OA}$を用いて表すことができますね．

この記事では，

内積を用いた三角形の面積公式
$xy$平面上での公式

を順に説明します．

「ベクトル」の一連の記事

内積を用いた三角形の面積公式
1. 公式と証明
2. 具体例（辺の長さと内積が分かっている場合）
$xy$平面上での公式
1. 公式と証明
2. 具体例（３頂点の座標が分かっている場合）

内積を用いた三角形の面積公式

まずは内積を用いた三角形の面積公式を紹介し，簡単な具体例を考えましょう．

公式と証明

三角形$\mrm{OAB}$おいて，$\ve{a}=\Ve{OA}$, $\ve{b}=\Ve{OB}$とする．

このとき，三角形$\mrm{OAB}$の面積$S$は

$\begin{align*}S=\frac{1}{2}\sqrt{|\ve{a}|^2|\ve{b}|^2-(\ve{a}\cdot\ve{b})^2}\end{align*}$

である．

三角形$\mrm{OAB}$の面積$S$は

$\begin{align*}S&=\frac{1}{2}\mrm{OA}\cdot\mrm{OB}\sin{\ang{O}} \\&=|\ve{a}||\ve{b}|\sin{\theta}\end{align*}$

と表せる．$0^\circ<\theta<180^\circ$だから$\sin{\theta}=\sqrt{1-\cos^2{\theta}}$なので，さらに

$\begin{align*}S=\frac{1}{2}|\ve{a}||\ve{b}|\sqrt{1-\cos^2{\theta}} =\frac{1}{2}\sqrt{|\ve{a}|^2|\ve{b}|^2-(|\ve{a}||\ve{b}|\cos{\theta})^2}\end{align*}$

と変形できる．よって，内積の定義

$\begin{align*}\ve{a}\cdot\ve{b}=|\ve{a}||\ve{b}|\cos{\theta}\end{align*}$

と併せて

$\begin{align*}S=\frac{1}{2}\sqrt{|\ve{a}|^2|\ve{b}|^2-(\ve{a}\cdot\ve{b})^2}\end{align*}$

が成り立つ．

この公式から三角形$\mrm{OAB}$の面積は２辺のベクトル$\Ve{OA}$, $\Ve{OB}$の長さと内積が分かれば求まるということは意識しておきましょう．

具体例（辺の長さと内積が分かっている場合）

簡単な具体例を考えましょう．

$\mrm{AB}=2$, $\mrm{AC}=3$, $\Ve{AB}\cdot\Ve{AC}=-2$の三角形$\mrm{ABC}$の面積を求めよ．

$\Ve{AB}$, $\Ve{AC}$の長さと内積が分かっているので，内積を用いた三角形の面積公式が使えますね．

ベクトルの三角形の面積公式より，

$\begin{align*}\tri{ABC} &=\frac{1}{2}\sqrt{\mrm{AB}^2\cdot\mrm{AC}^2-(\Ve{AB}\cdot\Ve{AC})^2} \\&=\frac{1}{2}\sqrt{2^2\cdot3^2-(-2)^2} =\frac{1}{2}\sqrt{32} =2\sqrt{2}\end{align*}$

である．

$xy$平面上での公式

$xy$平面で上で示した三角形の面積公式を考えると，とても簡単な形になります．

公式と証明

$xy$平面上の三角形$\mrm{ABC}$を考える．$\Ve{AB}\pmat{b_1\\b_2}$, $\Ve{AC}\pmat{c_1\\c_2}$とおくと，三角形$\mrm{OAB}$の面積$S$は

$\begin{align*}S=\frac{1}{2}|b_1c_2-b_2c_1|\end{align*}$

である．

$\ve{b}=\Ve{AB}$, $\ve{c}=\Ve{AC}$の長さと内積は

$|\ve{b}|^2={b_1}^2+{b_2}^2$
$|\ve{c}|^2={c_1}^2+{c_2}^2$
$\ve{b}\cdot\ve{c}=b_1c_1+b_2c_2$

なので，

$\begin{align*}&|\ve{b}|^2|\ve{c}|^2-(\ve{b}\cdot\ve{c})^2 \\&=({b_1}^2{c_1}^2+{b_1}^2{c_2}^2+{b_2}^2{c_1}^2+{b_2}^2{c_2}^2)-({b_1}^2{c_1}^2+2+b_1c_1b_2c_2+{b_2}^2{c_2}^2) \\&={b_1}^2{c_2}^2-2b_1c_1b_2c_2+{b_2}^2{c_1}^2 \\&=(b_1c_2-b_2c_1)^2\end{align*}$

である．よって，三角形の面積公式より

$\begin{align*}S&=\frac{1}{2}\sqrt{|\ve{b}|^2|\ve{c}|^2-(\ve{b}\cdot\ve{c})^2} \\&=\frac{1}{2}\sqrt{(b_1c_2-b_2c_1)^2}=\frac{1}{2}|b_1c_2-b_2c_1|\end{align*}$

を得る．

この公式から$xy$平面上の三角形$\mrm{ABC}$の面積は２辺のベクトル$\Ve{AB}$, $\Ve{BC}$が成分で表せられれば求まるということは意識しておきましょう．

具体例（３頂点の座標が分かっている場合）

$xy$平面上の３点$\mrm{A}(1,2)$, $\mrm{B}(3,-1)$, $\mrm{C}(-3,0)$を頂点とする三角形$\mrm{ABC}$の面積を求めよ．

各頂点の座標より

$\begin{align*}&\Ve{AB}=\pmat{3-1\\-1-2}=\pmat{2\\-3}, \\&\Ve{AC}=\pmat{-3-1\\0-2}=\pmat{-4\\-2}\end{align*}$

だから，$xy$平面での三角形の面積公式より

$\begin{align*}\tri{ABC}=&\frac{1}{2}|2\cdot(-2)-(-3)\cdot(-4)|=8\end{align*}$

である．

この問題のように，$xy$平面上の三角形$\mrm{OAB}$の３頂点の座標が分かっていれば，２辺のベクトル$\Ve{OA}$, $\Ve{OB}$の成分が分かり面積が求まるということは意識しておきましょう．