ベクトルを使えば図形的な考察をしなくても，計算によって解けることも多く図形問題ではとても心強い道具です．
しかし，図形が苦手な人はその苦手意識からベクトルも苦手になってしまうのはもったいないところで，図形が苦手な人ほどベクトルをしっかり学びたいところです．
また，ベクトルの基礎事項はそれほど多くなく，それらを繰り返し使っていくだけなので，実はコストパフォーマンスの良い分野でもあります．
なお，高校物理で扱うベクトルは簡単なものに限られますが，大学以上の物理ではベクトルを積極的に使って話を進めていきます．
そのため，とくに理系の人はベクトルをしっかり扱えるようにしておきたいところです．
「ベクトル」の一連の記事
ベクトルとは
まずはベクトルのイメージを掴みましょう．
ベクトルのイメージ
ボールを床に転がすと，そのボールの転がる向きを矢印で表現することができますね．例えば，
- 下図では，矢印が長いAの方がの方が速く転がっているように感じます．
- 下図では，異なる方向にボールが転がっているように感じます．
このように，矢印１本で
- 大きさ
- 向き
を同時に表現できるわけですね．
ベクトル
この矢印こそまさにベクトルで次のように定義します．
ベクトル (vector)とは
- 向き (direction)
- 長さ (length)
の２つを併せたものをいい，有向線分（矢印）で表す．
点$\mrm{A}$から点$\mrm{B}$へ向かう有向線分(矢印)を$\Ve{AB}$と表し，Aを始点 (start point)，Bを終点 (end point)という．
また，$\Ve{AA}$のように始点と終点が一致するベクトルを零ベクトル (zero vector)といい，$\Ve{0}$と表す．
ベクトルは「向き」と「長さ」をもっているものなので，平行移動して一致する矢印は同じベクトルとみなします．
つまり，上図においては$\Ve{AB}=\Ve{CD}$となるわけですね．
ベクトルの長さ
ベクトルの長さを以下の記号で表します．
ベクトル$\Ve{AB}$の長さを$|\Ve{AB}|$と表す．
また，長さが１のベクトルを単位ベクトル (unit vector)という．
$|\ve{a}|$は「ベクトル$\ve{a}$の長さ」と読みます．
絶対値の記号$|\quad|$と同じ記号で（絶対値と同じイメージで）はありますが，「絶対値」とは読みません．
ベクトルの計算
次に
- ベクトルに実数をかける
- ベクトルの和と差
といったベクトルの計算について説明します．
ベクトルに実数をかける
ベクトルに実数をかけてできるベクトルを以下のように定義します．
正の数$k$とベクトル$\ve{a}$に対して，
- $k\ve{a}$を$\ve{a}$の向きはそのままにし，長さを$k$倍したベクトルと定め，
- $-k\ve{a}$を$\ve{a}$の向きを逆向きにし，長さを$k$倍したベクトルと定める．
また，$0\ve{a}=\ve{0}$と定める．さらに，$(-1)\ve{a}$を$-\ve{a}$と表し，$\ve{a}$の逆ベクトル (inverse vector)という．
例えば，下図のようになりますね．
平行なベクトル
２つのベクトル$\ve{a}$, $\ve{b}$について，一方のベクトルを引き伸ばしたり縮めたりして他方のベクトルと等しくなるとき，２つのベクトルは平行であるといいます．
きちんと定義を書くと以下のようになります．
零ベクトルでないベクトル$\ve{a}$, $\ve{b}$に対して，
を満たす実数$k$が存在するとき，$\ve{a}$と$\ve{b}$は平行 (parallel)であるという．
図形の平行と同じイメージですが，このように等式で表せるのがベクトルの良いところです．
単位ベクトル
零ベクトルでないベクトル$\ve{a}$のベクトルの長さは$|\ve{a}|$なので，$\ve{a}$に$\dfrac{1}{|\ve{a}|}$をかけると長さが１のベクトルとなります．
また，$\ve{a}$に平行な単位ベクトルは$\ve{a}$に同じ向きのものと逆向きのものがありますから，以下が成り立ちます．
零ベクトルでないベクトル$\ve{a}$に対して，$\ve{a}$平行な単位ベクトルは$\dfrac{1}{|\ve{a}|}\ve{a}$, $-\dfrac{1}{|\ve{a}|}\ve{a}$は$\ve{a}$である．
ベクトルの和と差
ベクトルの和は以下のように定義します．
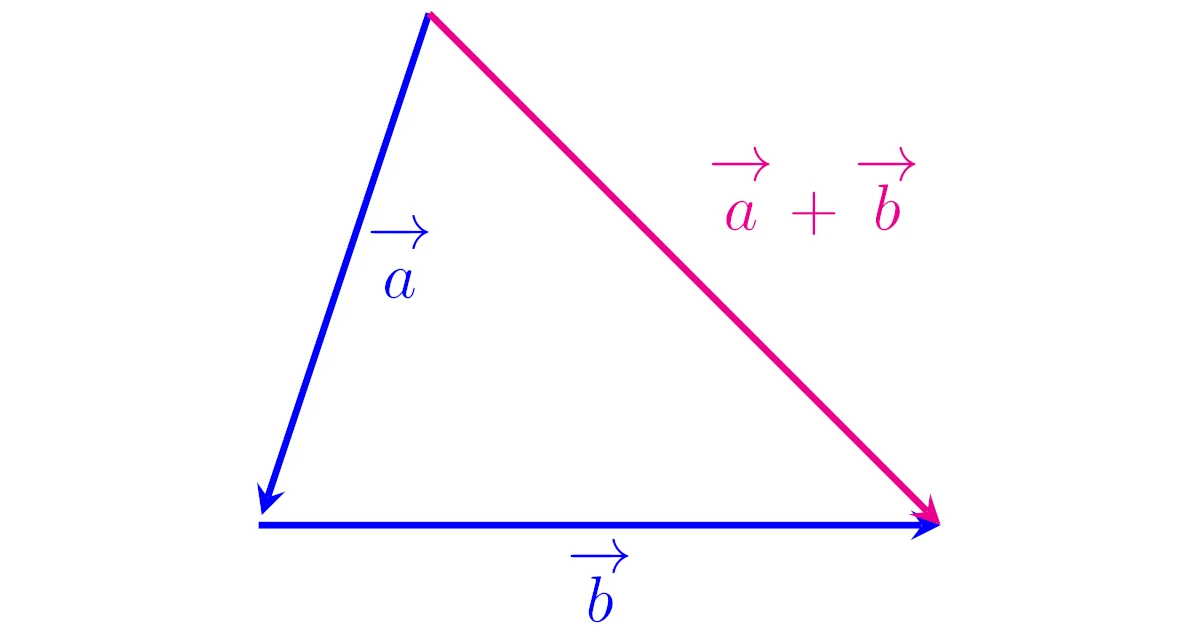
ベクトル$\ve{a}$, $\ve{b}$に対して，$\ve{a}$の終点と$\ve{b}$を一致させたとき，$\ve{a}+\ve{b}$を
- 「$\ve{a}$の始点」を$\ve{a}+\ve{b}$の始点
- 「$\ve{b}$の終点」を$\ve{a}+\ve{b}$の終点
とするベクトルと定める．
また，$\ve{a}-\ve{b}=\ve{a}+(-\ve{b})$と定める．
つまり，
- 和$\ve{a}+\ve{b}$は$\ve{a}$の矢印と$\ve{b}$の矢印を繋げてできるベクトル
- 差$\ve{a}-\ve{b}$は$\ve{a}$の矢印と$\ve{b}$の逆ベクトル$-\ve{b}$の矢印を繋げてできるベクトル
と定義するわけですね．
直交座標上のベクトル
平面図形を適当に$xy$平面におくことで座標計算ができて便利になることも多かったように，平面上のベクトルも$xy$平面上で考えることで計算が便利になることはよくあります．
ベクトルの表し方
$xy$平面上のベクトルは次のように成分で表します．
$xy$平面上の２点$\mrm{A}(a_1,a_2)$, $\mrm{B}(b_1,b_2)$に対して，$\Ve{AB}$を
または
と表す．
高校数学の教科書では後者のように座標のように表すことが多いですが，大学以降では前者のように縦に成分を並べて表すことも多いです．
ベクトルの計算をするときには縦に成分を並べた方が見やすいので，このブログの記事ではこの前者の縦に成分を並べてベクトルを表します．
さて，上の定義から分かるように，$xy$平面上のベクトル$\pmat{a\\b}$は
- $x$軸方向にちょうど$+a$の長さ
- $y$軸方向にちょうど$+b$の長さ
を持つベクトルというわけですね．
$xy$平面上の２点間の距離（ほとんど三平方の定理）より，座標上のベクトルの長さについては，以下のようになりますね．
$xy$平面上のベクトル$\ve{x}=\pmat{a\\b}$に対して，
である．
ベクトルの計算
上でみた
- 実数をベクトルにかける
- ベクトルとベクトルの和，差をとる
ということを$xy$平面上で考えると，以下のようになりますね．
実数$k$と$xy$平面上のベクトル$\ve{a}=\pmat{x\\y}$に対して，
である．
$xy$平面上のベクトル$\ve{a}=\pmat{a_1\\a_2}$, $\ve{b}=\pmat{b_1\\b_2}$に対して，
である．
コメント