「壁に立てかけた棒が倒れる」など,物体の回転が関わる運動では物体の大きさを無視できず,このように物体の大きさを考慮する物体を剛体というのでした.
剛体に複数の力がはたらいているとき,合力の力のモーメントを考える際には,はたらいている力の合成を考えることになります.
しかし,質点の場合とは違って剛体に複数の力がはたらく場合には,それらの力の作用点が異なることが多いです.
この記事では,剛体に作用点が異なる複数の力がはたらいている場合の力の合成を
- 平行でない2つの力
- 平行で同じ向きの2つの力
- 平行で逆向きの2つの力(大きさが異なる場合)
- 平行で逆向きの2つの力(大きさが等しい場合)
の4パターンに分けて説明します.
「剛体の運動」の一連の記事
平行でない2力の合成
剛体にはたらいている2力が平行でないときが最も簡単で,次のようになります.
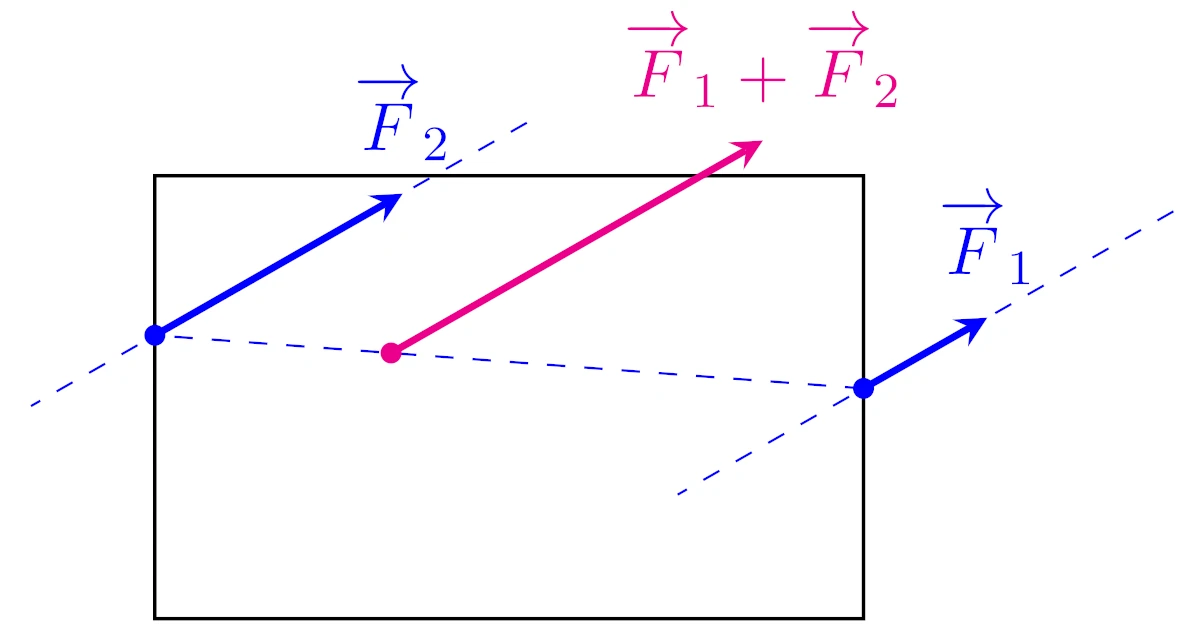
剛体にはたらく力$\ve{F}_1$, $\ve{F}_2$が平行でないとき,これらの合成は次のようになる.
- 作用点:$\ve{F}_1$の作用線と$\ve{F}_2$の作用線の交点
- 力:$\ve{F}_1+\ve{F}_2$
力$\ve{F}_1,\ve{F}_2$が平行でなければ,力$\ve{F}_1$の作用線と力$\ve{F}_2$の作用線が交点をもち,合力$\ve{F}$の作用点はこの作用線の交点となるわけですね.
また,合力は単純に$\ve{F}_1$と$\ve{F}_2$の和となり,大きさと向きについても単純ですね.
平行で同じ向きの2力の合成
平行な2力$\ve{F}_1$, $\ve{F}_2$の作用線は交点を持ちませんから,上で考えた$\ve{F}_1$, $\ve{F}_2$のようには考えることができません.
平行な2力が同じ向きのときは以下のように合成されます.
剛体にはたらく力$\ve{F}_1$, $\ve{F}_2$が平行で同じ向きのとき,これらの合成は次のようになる.
例えば,$|\ve{F}_1|$が$|\ve{F}_2|$に比べて非常に大きいときを考えれば,剛体にはたらく力はほとんど$\ve{F}_1$だけですね.
こう考えると,$\ve{F}_1$, $\ve{F}_2$が平行で向きが同じときは,$ve{F}_1$の作用点と$ve{F}_2$の作用点を結んだ線分を逆比に($|\ve{F}_2|:|\ve{F}_1|$に)内分する点が作用点となることは自然に思えますね.
また,合力は単純に$\ve{F}_1$と$\ve{F}_2$の和となり,大きさと向きについても単純ですね.
平行で逆向きの2力の合成
この場合は2力の大きさが異なるときと等しいときで様子が変わります.
2力の大きさが異なるとき
剛体にはたらく2力が平行で逆向きで大きさが異なるとき,力の合成は次のようになります.
剛体にはたらく力$\ve{F}_1$, $\ve{F}_2$が平行で逆向きで大きさが異なるとき,これらの合成は次のようになる.
(図は$|\ve{F}_1|>|\ve{F}_2|$の場合)
2力が平行で同じ向きのときと似ていますが,逆向きの場合の作用点は外分になります.
また,$\ve{F}_1$と$\ve{F}_2$は逆向きなので,合力は$\ve{F}_1+\ve{F}_2$は$\ve{F}_1$と$\ve{F}_2$の大きい方と同じ向きになりますね.
2力の大きさが等しいとき
剛体にはたらく2力が平行で逆向きで大きさが等しいとき,2力は剛体をただ回転させる作用のみとなります.
このときの2力のことを偶力といい,偶力の剛体を回転させる強さのことを偶力のモーメントといいます.
偶力のモーメントは次のようになります.
剛体にはたらく力$\ve{F}_1$, $\ve{F}_2$が平行で逆向きで大きさが等しいとき,力$\ve{F}_1$の作用線と力$\ve{F}_2$の作用線の距離を$\ell[\mrm{m}]$とし,$\ve{F}_1$, $\ve{F}_2$の大きさを$F[\mrm{N}]$とすると,偶力のモーメントは$F\ell[\mrm{Nm}]$である.
偶力のモーメントは作用点の中点を回転軸としたときの$\Ve{F}_1,\Ve{F}_2$の力のモーメントの和と言っても良いですね.
コメント