角度$\theta$が$0^\circ\leqq\theta\leqq180^\circ$のときの三角比$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$は，$xy$平面上の単位円を用いて定義するのでした．
この３つの三角比のうち$\tan{\theta}$は
で定義されるのでした．
この定義から$\tan{\theta}$は$xy$平面上の（$y$軸に平行でない）直線の傾きを表すという図形的な捉え方ができます．
この記事では
- $\tan{\theta}$の図形的な捉え方
- $xy$上の直線がなす角の具体例
を順に解説します．
「三角比」の一連の記事
$\tan{\theta}$の図形的な捉え方
ここで$\tan{\theta}$の図形的な意味を$xy$平面上で考えておきましょう．
原点を通る直線の傾き
点$\mrm{P}(\cos{\theta},\sin{\theta})$（$0^\circ\leqq\theta\leqq180^\circ$）について，$\cos{\theta}\neq0$のときの原点$\mrm{O}(0,0)$と点$\mrm{P}$を通る直線の傾きは
なのでした．すなわち，直線$\mrm{OP}$は$x$軸方向に$1$増加すると$y$軸方向に$\tan\theta$増加します．
よって，$xy$平面上の直線$x=1$と直線$\mrm{OP}$の交点の$y$座標が$\tan\theta$となりますね．
［１］$0^\circ\leqq\theta<90^\circ$のとき
［２］$90^\circ<\theta\leqq180^\circ$のとき
直線が$x$軸とのなす角
いまは原点を通る直線に対して考えましたが，平行移動して考えれば原点を通らない直線に対しても同様のことが成り立ちます．
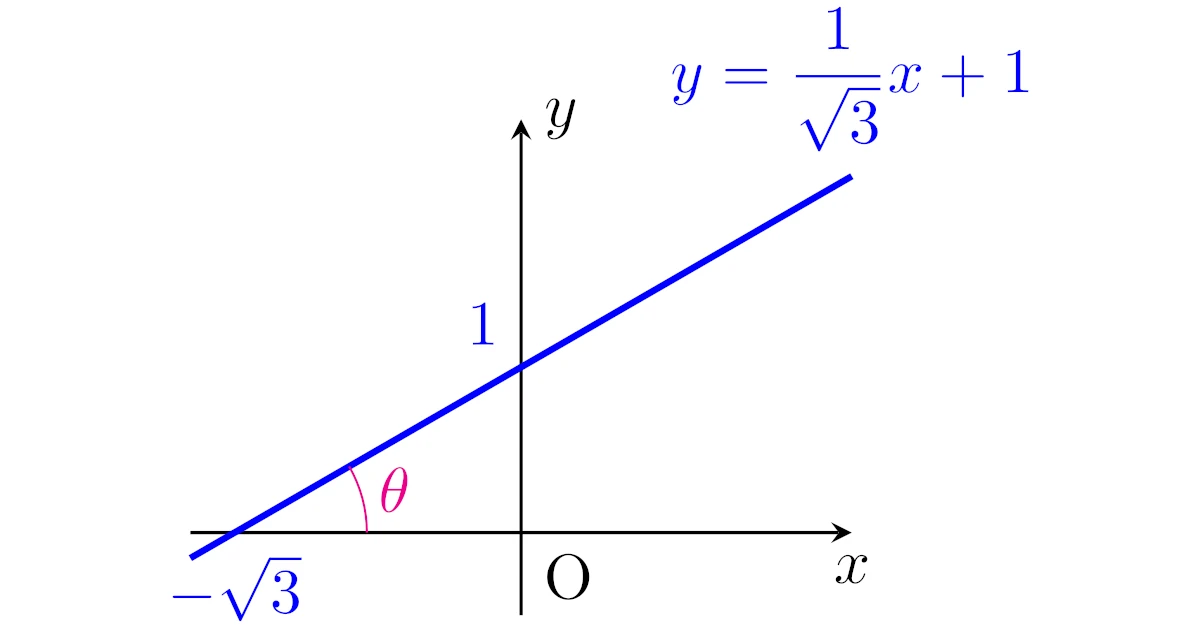
$xy$平面上の直線$\ell$を考える．下図のように直線$\ell$と$x$軸の正方向とのなす角が$\theta$のとき，直線$\ell$の傾きは$\tan{\theta}$である．
［１］$0^\circ\leqq\theta<90^\circ$のとき
［２］$90^\circ<\theta\leqq180^\circ$のとき
点$\mrm{P}$を$(\cos{\theta},\sin{\theta})$とすると，直線$\mrm{OP}$と直線$\ell$は同位角が等しいので平行です．
［１］$0^\circ\leqq\theta<90^\circ$のとき
［２］$90^\circ<\theta\leqq180^\circ$のとき
いま，直線$\mrm{OP}$の傾きは
なので，直線$\ell$の傾きも$\tan{\theta}$となります．
$xy$平面上の直線がなす角の具体例
いくつか具体例を考えましょう．
具体例１（直線と$x$軸がなす角）
$xy$平面上の直線$y=x+1$と$x$軸正方向とのなす角$\theta$の大きさを求めよ．ただし，角$\theta$は$y$軸正側とする．
直線$y=x+1$の傾きは$1$だから，
である．$0^\circ\leqq\theta\leqq180^\circ$だから$\theta=45^\circ$である．
具体例２（直線と$x$軸がなす角）
$xy$平面上の直線$y=-\sqrt{3}x+2$と$x$軸正方向とのなす角$\theta$の大きさを求めよ．ただし，角$\theta$は$y$軸正側とする．
直線$y=-\sqrt{3}x+2$の傾きは$-\sqrt{3}$だから，
である．$0^\circ\leqq\theta\leqq180^\circ$だから$\theta=120^\circ$である．
具体例３（２直線のなす角）
$xy$平面上の２直線$y=x+1$, $y=-\sqrt{3}x+2$のなす角$\theta$の大きさを求めよ．ただし，角$\theta$は$90^\circ$未満の側とする．
２本の直線を平行移動してもなす角は変わらないから，$y=x$, $y=-\sqrt{3}x$のなす角$\theta$の大きさを求めればよい（$\theta<90^\circ$）．
例１で求めたことより$y=x$と$x$軸正方向となす角（$y$軸正側）の大きさは$45^\circ$で， 例２で求めたことより$y=-\sqrt{3}x$と$x$軸正方向となす角（$y$軸正側）の大きさは$120^\circ$だから，
である．
コメント