図形と方程式６<br>２種類の円の方程式をマスターしよう

前回の記事までは$xy$平面上の点や直線について説明してきました．

今回の記事からは$xy$平面上の円について考えていきましょう．

一般に$xy$平面上の円の方程式を表す際には

平方完成型$(x-a)^2+(y-b)^2=r^2$
展開型$x^2+y^2+Ax+By+C=0$

のどちらかで表すことが多いです．

この記事では

円の定義の確認
２種類の円の方程式

を順に説明します．

「図形と方程式」の一連の記事

円の定義の確認
円の方程式
1. 平方完成型
2. 展開型の円の方程式
展開型の円の方程式の注意点

円の定義の確認

まずは円の定義を確認しておきましょう．

$r>0$とする．平面上の図形$\mrm{C}$が半径$r$の円であるとは，ある１点$\mrm{O}$と図形$\mrm{C}$上の全ての点との距離が$r$であることをいう．

また，このときの点$\mrm{O}$を円$\mrm{C}$の中心という．

要するに「ある１点からの距離が等しい点を集めてできる図形」を円というわけですね．

さて，コンパスで円を描くときは

コンパスを広げる（半径を決める）
紙に針を刺す（中心を決める）

という手順を踏むように，「中心と半径を決めれば円はひとつに決まる」ということは意識しておきましょう．

円の方程式

$xy$平面上の[円の方程式]には

平方完成型
展開型

の２種類があります．

平方完成型

まずは平方完成型の円の方程式から説明します．

[円の方程式]　$a$, $b$は実数，$r$は正の数とする．$xy$平面上の中心$(a,b)$，半径$r$の円の方程式は

$\begin{align*}(x-a)^2+(y-b)^2=r^2\quad \dots (*)\end{align*}$

と表される．

ベースとなる考え方は２点間の距離です．

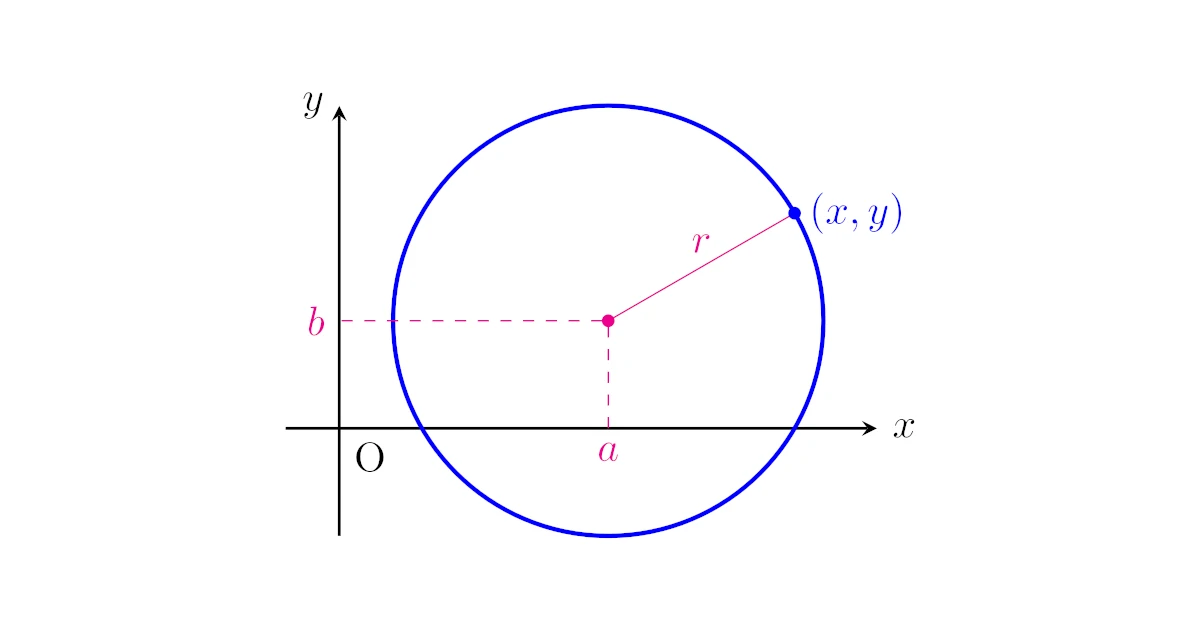
$xy$平面上の中心$(a,b)$，半径$r$の円に対して，円周上の点$(x,y)$と中心$(a,b)$の距離は$r$だから

$\begin{align*}\sqrt{(x-a)^2+(y-b)^2}=r\end{align*}$

が成り立つ．

両辺とも常に正なので，$2$乗しても同値で

$\begin{align*}(x-a)^2+(y-b)^2=r^2\quad \dots (*)\end{align*}$

を得る．

逆に方程式$(*)$が表す$xy$平面上のグラフ上の点を$(x,y)$とすると，今の議論を逆に辿って点$(x,y)$は中心$(a,b)$，半径$r$の円周上に存在する．

この証明は「円は１点から等距離にある点の集めてできる図形」という円の定義に従っていますが，本質的には３点$(a,b)$, $(x,y)$, $(a,y)$を頂点とする直角三角形に三平方の定理を適用したものになっています．

また，$a=b=0$とすると原点中心の円を考えることになるので，原点中心の円の方程式は以下のようになることも当たり前にしておきましょう．

[原点中心の円の方程式]　$r$は正の数とする．$xy$平面上の原点中心，半径$r$の円の方程式は

$\begin{align*}x^2+y^2=r^2\end{align*}$

と表される．

展開型の円の方程式

次に展開型の円の方程式を説明します．

中心$(a,b)$，半径$r$の円の方程式$(x-a)^2+(y-b)^2=r^2$を展開すると，

$\begin{align*}x^2-2ax+y^2-2by+\bra{a^2+b^2-r^2}=0\end{align*}$

となることから，円は

$\begin{align*}x^2+y^2+Ax+By+C=0\quad\dots(*)\end{align*}$

の形の方程式でも表すことができます．

次の$x$, $y$の方程式が表す$xy$平面上のグラフを求めよ．

$x^2+y^2-2y-3=0$
$x^2+y^2-2x+4y=4$
$x^2+y^2-x-y=0$

(1)　$x^2+y^2-2y-3=0$の左辺を平方完成して

$\begin{align*}&x^2+y^2-2y-3=0 \\\iff&x^2+(y^2-2y+1)-4=0 \\\iff&x^2+(y-1)^2=2^2\end{align*}$

と平方完成型の円の方程式になるので，グラフは中心$(0,1)$，半径$2$の円である．

(2)　$x^2+y^2-2x+4y=4$の左辺を平方完成して

$\begin{align*}&x^2+y^2-2x+4y=4 \\\iff&(x^2-2x+1)+(y^2+4y+4)=9 \\\iff&(x-1)^2+(y+2)^2=3^2\end{align*}$

と平方完成型の円の方程式になるので，グラフは中心$(1,-2)$，半径$3$の円である．

(3)　$x^2+y^2-x-y=0$の左辺を平方完成して

$\begin{align*}&x^2+y^2-x-y=0 \\\iff&\bra{x^2-x+\frac{1}{4}}+\bra{y^2-y+\frac{1}{4}}=\frac{1}{2} \\\iff&\bra{x-\frac{1}{2}}^2+\bra{y-\frac{1}{2}}^2=\bra{\frac{1}{\sqrt{2}}}^2\end{align*}$

と平方完成型の円の方程式になるので，グラフは中心$\bra{\dfrac{1}{2},\dfrac{1}{2}}$，半径$\dfrac{1}{\sqrt{2}}$の円である．

このように，展開型の円の方程式のままでは中心も半径も分からないので，平方完成型に変形して中心と半径を求めることができるわけですね．

展開型の円の方程式の注意点

ただし，$x^2+y^2+Ax+By+C=0$の形の方程式のグラフがいつでも円になるかというとそうではありません．

このことを見るために，もう少し問題を考えてみましょう．

次の$x$, $y$の方程式が表す$xy$平面上のグラフを求めよ．

$x^2+y^2-2x-6y+10=0$
$x^2+y^2-4x-2y+6=0$

(1)　$x^2+y^2-2x-6y+10=0$の左辺を平方完成して

$\begin{align*}&x^2+y^2-2x-6y+10=0 \\\iff&(x-2x+1)+(y-6y+9)=0 \\\iff&(x-1)^2+(y-3)^2=0\end{align*}$

となるので，この方程式を満たす$(x,y)$は$(x,y)=(1,3)$のみである．よって，この方程式が表すグラフは１点$(1,3)$を表す．

(2)　$x^2+y^2-4x-2y+6=0$の左辺を平方完成して

$\begin{align*}&x^2+y^2-4x-2y+4=0 \\\iff&(x^2-4x+4)+(y^2-2y+1)=-1 \\\iff&(x-1)^2+(y-3)^2=-1\end{align*}$

となる．左辺は$2$乗和だから常に$0$以上なので，$-1$になることはない．よって，この方程式を満たす$(x,y)$は存在しないから，この方程式が表すグラフは空集合である．

そもそも$x$, $y$の方程式のグラフとは，その方程式をみたす点$(x,y)$の集合のことなのでした．

よって，(3)のように１つの組$(x,y)$に対してのみ方程式を満たす場合は１点のみのグラフとなりますし，(4)のようにどんな組$(x,y)$に対しても方程式を満たさない場合はグラフは空集合になるわけですね．

図形と方程式２
「方程式が表すグラフ」ってそもそも何？

y=2x+1やy=-x+3のようなx,yの等式はxy平面上の直線を表すように，一般にx,yの等式はxy平面上のグラフを表します．この記事では，「方程式が表すグラフ」「グラフの平行移動」を順に説明します．

このように，方程式

$\begin{align*}x^2+Ax+y^2+By+C=0\end{align*}$

は必ずしも円とはなり得ないことを注意しておきましょう．

図形と方程式６
２種類の円の方程式をマスターしよう