　【SPONSORED LINK】

図形と方程式８｜円の接線の方程式は一発で求めよう！

2016/6/2 2020/5/25 図形と方程式

前回の記事では，どのようなときに

直線と円がちょうど２つ共有点をもつ
直線と円がちょうど１つ共有点をもつ(接する)
直線と円が共有点をもたない

となるのかについて説明しました．

２つめのパターンの「直線と円がちょうど１つの共有点をもつ(接する)場合」について，実は$xy$平面において

円$C$の方程式
円周上の点Pの座標

が分かれば，円$C$の点Pでの接線の方程式が求められます．

この記事では，この接線の方程式の求め方を説明します．

一連の記事はこちら

【図形と方程式１｜座標の超基本「内分点」と「外分点」の計算】
【図形と方程式２｜「方程式が表すグラフ」ってそもそも何？】
【図形と方程式３｜直線の「傾き」の考え方を理解しよう！】
【図形と方程式４｜一般の直線の方程式と[平行・垂直条件]】
【図形と方程式５｜[２点間の距離]と[点と直線の距離]】
【図形と方程式６｜２種類の[円の方程式]をマスターしよう】
【図形と方程式７｜[円と直線の共有点]の２つの考え方とコツ】
【図形と方程式８｜円の接線の方程式は一発で求めよう！】←今の記事
【図形と方程式９｜２円の共有点を通る円と直線はどう求める？】

【SPONSORED LINK】

原点中心の円に接する直線

まずは原点中心，半径$r$の円$x^2+y^2=r^2$に接する直線の方程式は次で求められます．

[原点中心の円の接線]　原点O中心，半径$r$の円$C:x^2+y^2=r^2$ $(r>0)$に点$\mrm{P}(\alpha,\beta)$で接する直線$\ell$の方程式は

$\begin{align*} \ell:\alpha x+\beta y=r^2 \end{align*}$

である．

形としては，円の方程式$x^2+y^2=r^2$の

$x$を１つだけ$\alpha$に変えて
$y$を１つだけ$\beta$に変えたもの

になっていますね．

具体例

公式の導出の前に，具体例を見てみましょう．

次の円$C$と円$C$上の点Pについて，点Pでの円$C$の接線の方程式を求めよ．

$C:x^2+y^2=4$，$\mrm{P}(1,\sqrt{3})$
$C:x^2+y^2=9$，$\mrm{P}(0,3)$
$C:x^2+y^2=2$，$\mrm{P}(-\sqrt{2},0)$

(1)　求める接線の方程式は

$\begin{align*} &1\cdot x+\sqrt{3}\cdot y=4 \\\iff& x+\sqrt{3}y=4 \end{align*}$

である．

(2)　求める接線の方程式は

$\begin{align*} &0\cdot x+3\cdot y=9 \\\iff& 3y=9 \\\iff& y=3 \end{align*}$

である．

(3)　求める接線の方程式は

$\begin{align*} &(-2)\cdot x+0\cdot y=4 \\\iff& -2x=4 \\\iff& x=-2 \end{align*}$

である．

$xy$平面上の円$C$の方程式と円$C$上の点Pの座標が与えられたとき，点Pでの円$C$の方程式は公式より直ちに求まる．

公式の導出

それでは公式を証明しましょう．

まずは直線OPの方程式を求めます．

[1]　$\alpha=0$のとき

直線OPは

原点$\mrm{O}(0,0)$を通り
傾きは$\dfrac{\beta}{\alpha}$なので

直線OPの方程式$y=\dfrac{\beta}{\alpha}x$ですから，分母を払って整理すると，

$\begin{align*} \mrm{OP}:\beta x-\alpha y=0\quad(*) \end{align*}$

となります．

[2]　$\alpha=0$のとき

点Pは$y$軸上に存在するので，直線OPの方程式は$x=0$と表せます．

また，点Aが円$C$上にあることから$\alpha$と$\beta$は同時に０にはならないから$\beta\neq0$なので，

$\begin{align*} x=0 \iff& \beta x=0 \\\iff& \beta x-\alpha y=0 \end{align*}$

となります．よって，[1]と同じく直線OPの方程式は$\beta x-\alpha y=0$となることが分かりました．

さて，

直線$\ell$は点$\mrm{P}(\alpha,\beta)$を通り，
直線$\ell$は点Pで円$C$に接しているので，直線$\ell$と直線OPは垂直

となるので，直線OPの方程式から直線$\ell$の方程式も得られますね．

直線$\ell$の方程式は点$\mrm{P}(\alpha,\beta)$を通り，直線$\mrm{OP}:\beta x-\alpha y=0$に垂直でしたから，直線$\ell$の方程式は

$\begin{align*} \ell:-(-\alpha) (x-\alpha)+\beta (y-\beta)=0 \end{align*}$

となります．点$\mrm{A}(\alpha,\beta)$が円$C:x^2+y^2=r^2$上の点であることから$\alpha^2+\beta^2=r^2$であることに注意すると，この直線$\ell$の方程式は

$\begin{align*} &\alpha(x-\alpha)+\beta(y-\beta)=0 \\\iff&\alpha x+\beta y=\alpha^2+\beta^2 \\\iff&\alpha x+\beta y=r^2 \end{align*}$

となり，公式が導出できましたね．

なお，「平行/垂直な直線」と「通る点」から直線の方程式を求める方法については，以下の記事を参照してください．

【図形と方程式４｜一般の直線の方程式と[平行・垂直条件]】

例えば，「直線$3x+5y=2$に平行で点$(1,2)$を通る直線の方程式」や「直線$-3x+6y=5$に垂直で点$(3,4)$を通る直線の方程式」をすぐに求められますか？「ある直線に平行/垂直で，ある点を通る直線の方程式」は$y=$の形に変形しなくても，数秒で求められる方法があります．

一般の中心の円に接する直線

次に，原点中心とは限らない円の場合の接線の方程式を考えます．

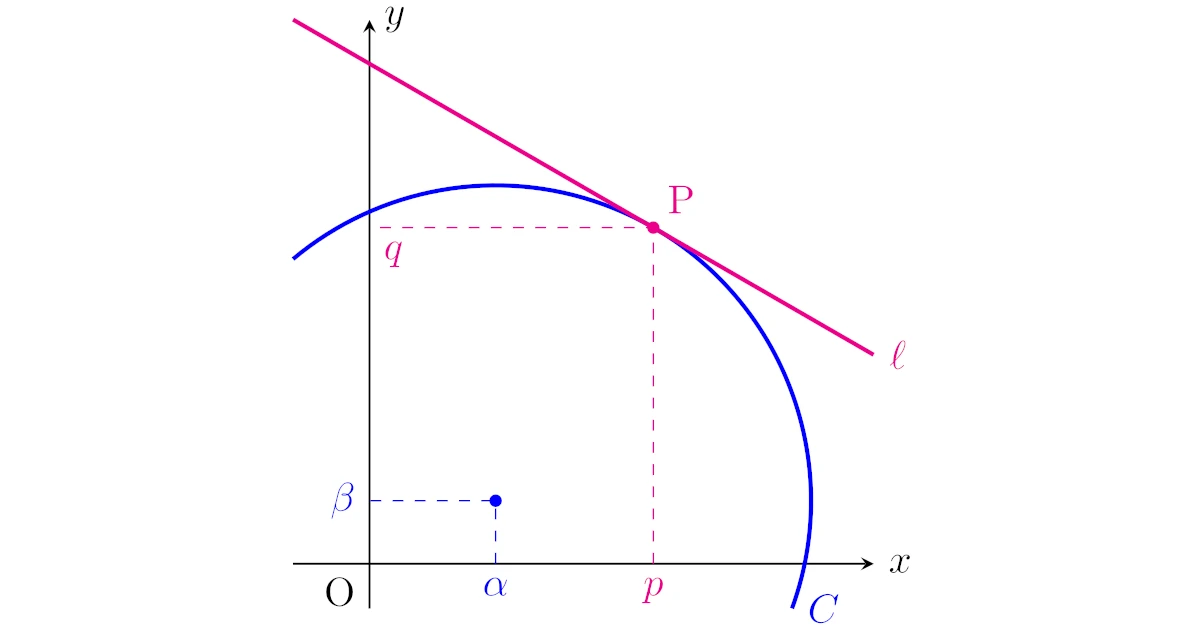
[一般の円の接線]　点$(p,q)$中心，半径$r$の円$C:(x-p)^2+(y-q)^2=r^2$に点$\mrm{P}(\alpha,\beta)$で接する直線$\ell$の方程式は次で得られる．

$\begin{align*} \ell:(\alpha-p)(x-p)+(\beta-q)(y-q)=r^2 \end{align*}$

先ほどの原点中心の円の場合と同じく，この場合にも円の方程式$(x-x_1)^2+(y-y_1)^2=r^2$の

$x$を１つだけ$\alpha$に変えて
$y$を１つだけ$\beta$に変えたもの

になっています．

導出は先ほどの原点中心の場合の結果で，$xy$平面上の平行移動を考えれば以下のように得られます．

円$(x-p)^2+(y-q)^2=r^2$は点$(p,q)$中心なので，

$x$軸方向に$-p$
$y$軸方向に$-q$

平行移動させると，原点中心の円$C’:x^2+y^2=r^2$となります．

同じ平行移動で点Pは$\mrm{P}'(\alpha-p,\beta-q)$に移動し，円$C’$の点P’での接線$\ell’$の方程式は[原点中心の円の接線]の公式より

$\begin{align*} \ell':(\alpha-p)x+(\beta-q)y=r^2 \end{align*}$

となります．この接線$\ell’$を先ほどの平行移動と逆に動かせば，求めたかった接線$\ell$になるので，接線$\ell$の方程式は

$\begin{align*} \ell:(\alpha-p)(x-p)+(\beta-q)(y-q)=r^2 \end{align*}$

となり，公式が導出できました．

【次の記事：図形と方程式９｜２円の共有点を通る円と直線はどう求める？】

２点A, Bで交わる２つの円について，この２交点A, Bを通る円や直線がすぐに求められることは実は教科書レベルです．次の記事では，２円の交点を通る円や直線の求め方を説明します．