集合$U$に属する要素$x$に関する条件$p$, $q$に対して，命題$p\Rightarrow q$を考えます．
条件$p$, $q$の否定をそれぞれ$\overline{p}$, $\overline{q}$で表すとき，命題$p\Rightarrow q$に対して，
- 命題$q\Rightarrow p$を逆
- 命題$\overline{p}\Rightarrow \overline{q}$を裏
- 命題$\overline{q}\Rightarrow \overline{p}$を対偶
といいます．
一般に「命題$\overline{q}\Rightarrow\overline{p}$の真偽とその対偶$\overline{p}\Rightarrow\overline{q}$の真偽は必ず一致する」ことが知られており，この性質を用いることで簡単に証明できる問題もあります．
この記事では
- 条件の否定
- 逆・裏・対偶
- 対偶を用いた証明
を順に説明します．
「論理と集合」の一連の記事
条件の否定
まずは条件の否定について説明します．
集合$U$の要素$x$に関する条件$p$に対して，「条件$p$を満たさない」という集合$U$の要素$x$に関する条件を$p$の否定という．
条件$p$の否定は$\overline{p}$と表すことが多く，この記事でも否定はこのように表します．
条件の否定は全体集合を意識することが大切です．このことを具体例から考えてみましょう．
具体例１
集合$U$を整数全部の集合とする．このとき，$U$の要素$x$に関する次の各条件$p$, $q$の否定を述べよ．
- $p$：$x$は偶数
- $q$：$x<1$または$4\le x$
(1)全体集合$U$は整数全部の集合なので，条件$p$の否定$\overline{p}$は「$x$は奇数」となる．
(2)全体集合$U$は整数全部の集合なので，条件$q$の否定$\overline{q}$は「$x=1,2,3$」となる．
具体例２
条件$p$, $q$自体は同じでも，全体集合が実数全体に変わると，条件の否定も変わります．
集合$U$を実数全部の集合とする．このとき，$U$の要素$x$に関する次の各条件$p$, $q$の否定を述べよ．
- $p$：$x$は偶数
- $q$：$x<1$または$4\le x$
(1)全体集合$U$は実数全部の集合なので，条件$p$の否定$\overline{p}$は「$x$は偶数でない実数」となる．
(2)全体集合$U$は実数全部の集合なので，条件$q$の否定$\overline{q}$は「$1\le x<4$」となる．
具体例１では全体集合が整数全部の集合なので「とびとび」でしたが，今回の具体例２では集合$U$が数直線全体です．
そのため，今回は$x=2.5$や$x=\pi$といった整数でないものも考えているので，このように答えが変わってくるわけですね．
逆，裏，対偶
それでは，命題$p\Rightarrow q$の逆・裏・対偶の説明に移りましょう．
逆・裏・対偶の定義
条件$p$, $q$に対して，
- 命題$q\Rightarrow p$を命題$p\Rightarrow q$の逆
- 命題$\overline{p}\Rightarrow\overline{q}$を命題$p\Rightarrow q$の裏
- 命題$\overline{q}\Rightarrow\overline{p}$を命題$p\Rightarrow q$の対偶
という．
例えば，$U$を整数全部の集合として，$U$の要素に関する条件$p$, $q$を
- $p$：$x$は$4$の倍数
- $q$：$x$は偶数
とすると，命題$p\Rightarrow q$は「整数$x$に対して，$x$が$4$の倍数なら$x$は偶数」ですね．
この命題$p\Rightarrow q$に対して，
- 逆は「整数$x$に対して，$x$が偶数なら$x$は$4$の倍数」
- 裏は「整数$x$に対して，$x$が$4$の倍数でないなら$x$は偶数でない」
- 対偶は「整数$x$に対して，$x$が偶数でないなら$x$は$4$の倍数でない」
となります．
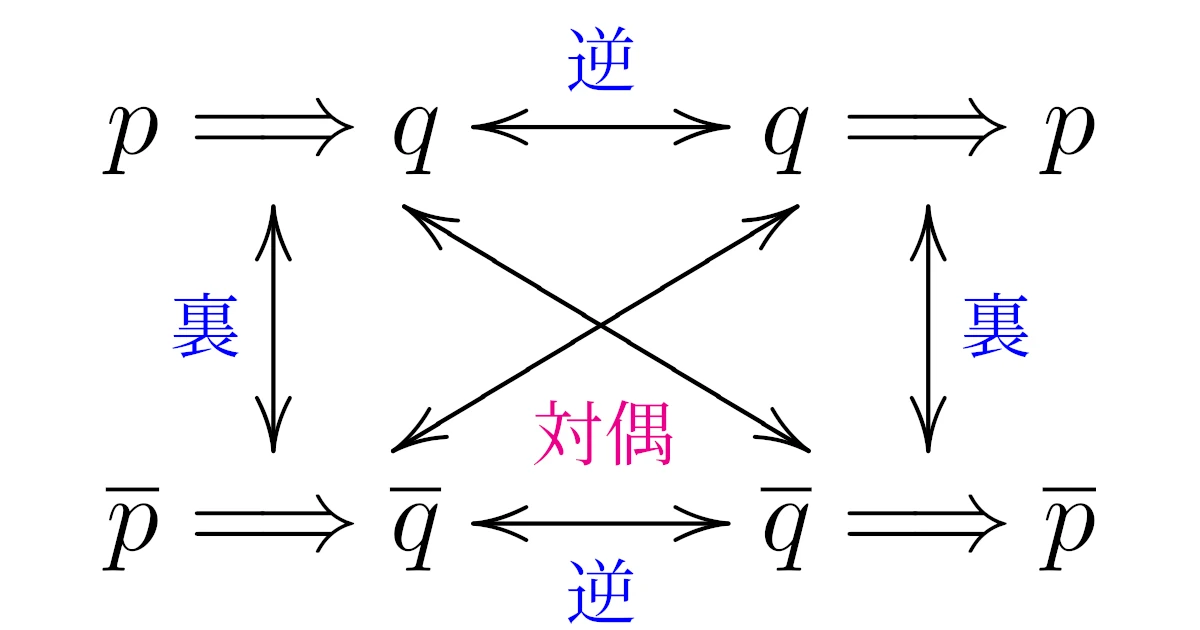
逆・裏・対偶の関係
例えば，「命題$p\Rightarrow q$の逆」の逆は元に戻って$p\Rightarrow q$となります．
他にも「命題$p\Rightarrow q$の逆」の裏は，対偶$\overline{q}\Rightarrow\overline{p}$となります．
このように，逆・裏・対偶には関係があり，下図のようになりますね．
逆・裏の注意点
逆・裏に関して，次のことに注意してください．
もとの命題が真であっても，逆・裏は真であるとは限らない．
例えば，上と同じく$U$を整数全部の集合として，$U$の要素に関する条件$p$, $q$を
- $p$：$x$は4の倍数である
- $q$：$x$は偶数である
とすると，命題$p\Rightarrow q$は真ですが
- 逆$q\Rightarrow p$は偽
- 裏$\overline{p}\Rightarrow\overline{q}$は偽
ですね．
対偶に関する定理
冒頭でも書いた通り，対偶について次の定理が成り立ちます．
条件$p$, $q$に対して，命題$p\Rightarrow q$の真偽とその対偶$\overline{q}\Rightarrow\overline{p}$の真偽は一致する．
つまり，
- $p\Rightarrow q$が真なら$\overline{q}\Rightarrow\overline{p}$も真
- $p\Rightarrow q$が偽なら$\overline{q}\Rightarrow\overline{p}$も偽
というわけですね．
証明
証明には前回の記事で説明した真理集合を用います．
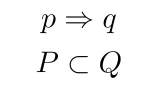
「命題の真偽」を「集合の包含」で考える話
条件$p$の真理集合を$P$，条件$q$の真理集合を$Q$とすると
- $p\Rightarrow q$が真
- $P\subset Q$
は同値である．また，このとき条件$\overline{p}$の真理集合は$P$の補集合$\overline{P}$，条件$q$の真理集合は$Q$の補集合$\overline{Q}$なので，
- $\overline{q}\Rightarrow\overline{p}$が真
- $\overline{Q}\subset\overline{P}$
は同値である．さらに，$P\subset Q$と$\overline{Q}\subset\overline{P}$は同値なので，結局
- $p\Rightarrow q$が真
- $\overline{q}\Rightarrow\overline{p}$が真
は同値となって，命題$p\Rightarrow q$とその対偶$\overline{q}\Rightarrow\overline{p}$の真偽は一致する．
対偶を利用した証明
この対偶の性質は次のような証明問題で有効です．
実数$x$, $y$が$x+y>0$をみたすなら，$x>0$または$y>0$であることを示せ．
２つの実数$(x,y)$の組全部の集合を$U$とし，$U$の要素$(x,y)$の条件$p$, $q$を
- $p$：$x+y>0$をみたす
- $q$：$x>0$または$y>0$をみたす
とすると，「$p\Rightarrow q$を示せ」ということになりますね．
これを直接示そうとするといくつか場合分けをする必要があって少々面倒ですが，対偶の性質を用いると簡単に証明することができます．
示すべき命題の対偶は「実数$x$, $y$が$x\leqq0$かつ$y\leqq0$をみたすとき，$x+y\leqq0$をみたす」である．
$x\leqq0$かつ$y\leqq0$なら辺々加えて$x+y\geqq0$なので，この対偶は真である．
一般にもとの命題とその対偶の真偽は一致するから，示すべき命題が成り立つことが分かった．
コメント