中学入試などでは,例えば
「$1,3,7,13,21,31,\square$の$\square$に入る数字を求めよ」
といった問題が出題されることがあります.
実はこれはまさに数列の問題で,これを詳しく扱っていくのが高校数学での数列です.
高校数学での数列で基礎となるのは
- 等差数列
- 等比数列
です.少し複雑な数列も等差数列または等比数列に帰着させることが多いので,この2つの数列はしっかり理解しておきましょう.
この記事では,これら
- 等差数列
- 等比数列
について説明します.
「数列」の一連の記事
数列の基本
まず,数列の基本から説明します.
数列とは
数列とは以下のものを言います.
数を一列に並べたものを数列という.数列の中でも
- 途中で終わる数列を有限数列
- 無限に続く数列を無限数列
という.
例えば,以下は全て数列です.
- $1,\ 3,\ 5,\ 7,\ 9,\ 11$
- $2,\ 3,\ 4,\ 5,\dots$
- $2,\ 4,\ 8,\ 16,\dots$
- $1,\ 1.4,\ 1.41,\ 1.414,\dots$
- $5,\ 168.2, -\pi,\ 25684,\dots$
最初のものは有限数列で,最初以外は全て無限数列ですね.
最後の数列には規則がなさそうに見えますが関係ありません.数が並んでいれば規則性があろうがなかろうが全て数列と言います.
数列の表し方
一般に,数列$a_1,\ a_2,\ a_3,\ \dots$を$\{a_n\}$と表します.
数列$\{a_n\}$について,$k$番目の数$a_k$を第$k$項という.また,第1項を初項といい,有限数列の最後の項を末項という.
さらに,任意の$n$に対して考える$a_n$を一般項という.
具体的に考えてみましょう.
次の数列を第3項まで求めよ.
- 一般項が$a_n=2n$の数列$\{a_n\}$
- 一般項が$b_n=\bra{-\frac{1}{2}}^n$の数列$\{b_n\}$
(1)$a_n=2n$に$n=1,2,3$を代入して
だから,初項から順に$2,4,6$である.
(2)$b_n=\bra{-\frac{1}{2}}^n$に$n=1,2,3$を代入して
だから,初項から順に$-\dfrac{1}{2},\dfrac{1}{4},-\dfrac{1}{8}$である.
等差数列と等比数列
数が並んでさえいれば規則性があろうがなかろうが全て数列ではありますが,めちゃくちゃな数列を考えてもよい結果は得られそうにないですね.
そこで,最も考えやすい基本的な数列として
- 等差数列
- 等比数列
があります.
等差数列
等差数列とは以下のような数列を指します.
1つ次の項に移るごとに,同じ数が足されている数列を等差数列という.また,このときに1つ次の項に移るごとに足されている数を公差という.
具体的にみてみましょう.
次の数列を第5項まで求めよ.
- 初項$1$,公差$1$の等差数列$\{a_n\}$
- 初項$3$,公差$1.5$の等差数列$\{b_n\}$
- 初項$7$,公差$-2$の等差数列$\{c_n\}$
(1)初項が$1$であることから$a_1=1$であり,これに公差$1$を加えていくと
だから,初項から順に$1,\ 2,\ 3,\ 4,\ 5$である.
(2)初項が$3$であることから$b_1=3$であり,これに公差$1.5$を加えていくと
だから,初項から順に$3,\ 4.5,\ 6,\ 7.5,\ 9$である.
(3)初項が$7$であることから$c_1=7$であり,これに公差$-2$を加えていくと
だから,初項から順に$7,\ 5,\ 3,\ 1,\ -1$である.
等比数列
等比数列も等差数列とほとんど同様に議論を進めることができます.
1つ次の項に移るごとに,同じ数がかけられている数列を等比数列という.また,このときに1つ次の項に移るごとにかけられている数を公比という.
具体的にみてみましょう.
次の数列を第5項まで求めよ.
- 初項$1$,公比$2$の等比数列$\{a_n\}$
- 初項$9$,公比$\dfrac{1}{3}$の等比数列$\{b_n\}$
- 初項$2$,公比$-2$の等比数列$\{c_n\}$
(1)初項が$1$であることから$a_1=1$であり,これに公比$2$をかけていくと
だから,初項から順に$1,\ 2,\ 4,\ 8,\ 16$である.
(2)初項が$9$であることから$b_1=9$であり,これに公比$\dfrac{1}{3}$をかけていくと
だから,初項から順に$9,\ 3,\ 1,\ \dfrac{1}{3},\ \dfrac{1}{9}$である.
(3)初項が$2$であることから$c_1=2$であり,これに公比$-2$をかけていくと
だから,初項から順に$2,\ -4,\ 8,\ -16,\ 32$である.
等差数列と等比数列の一般項
次に,等差数列と等比数列の一般項がどのように表せるかを考えましょう.
等差数列の一般項
初項$a$,公差$d$の等差数列は
- 初項は$a$
- 第2項は$a+d$
- 第3項は$a+2d$
- 第4項は$a+3d$
- ……
- 第100項は$a+99d$
- ……
と項が順に求まっていきます.このことから,次が成り立つことがみてとれますね.
初項$a$,公差$d$の等差数列$\{a_n\}$の一般項は
である.
このように,初項と公差が分かれば,等差数列の一般項が得られることは当たり前にしておきましょう.
また,逆に一般項が$a_n=a+(n-1)d$の数列$\{a_n\}$を考えると,
ですから$\{a_n\}$は初項$a$,公差$d$の等差数列になります.よって,上の定理の逆も成り立ちますね.
等比数列の一般項
初項$a$,公比$r$の等比数列は
- 初項は$a$
- 第2項は$ar$
- 第3項は$ar^2$
- 第4項は$ar^3$
- ……
- 第100項は$ar^99$
- ……
と項が順に求まっていきます.このことから,次が成り立つことがみてとれますね.
初項$a$,公比$d$の等比数列$\{a_n\}$の一般項は
である.
このように,初項と公比が分かれば,当比数列の一般項が得られることは当たり前にしておきましょう.
また,逆に一般項が$a_n=ar^{n-1}$の数列$\{a_n\}$を考えると,
ですから$\{a_n\}$は初項$a$,公比$r$の等比数列になります.よって,上の定理の逆も成り立ちますね.
等差数列と等比数列の違いは一定の数をかけていくか足していくかだけで,並行に話を進めることができますね.
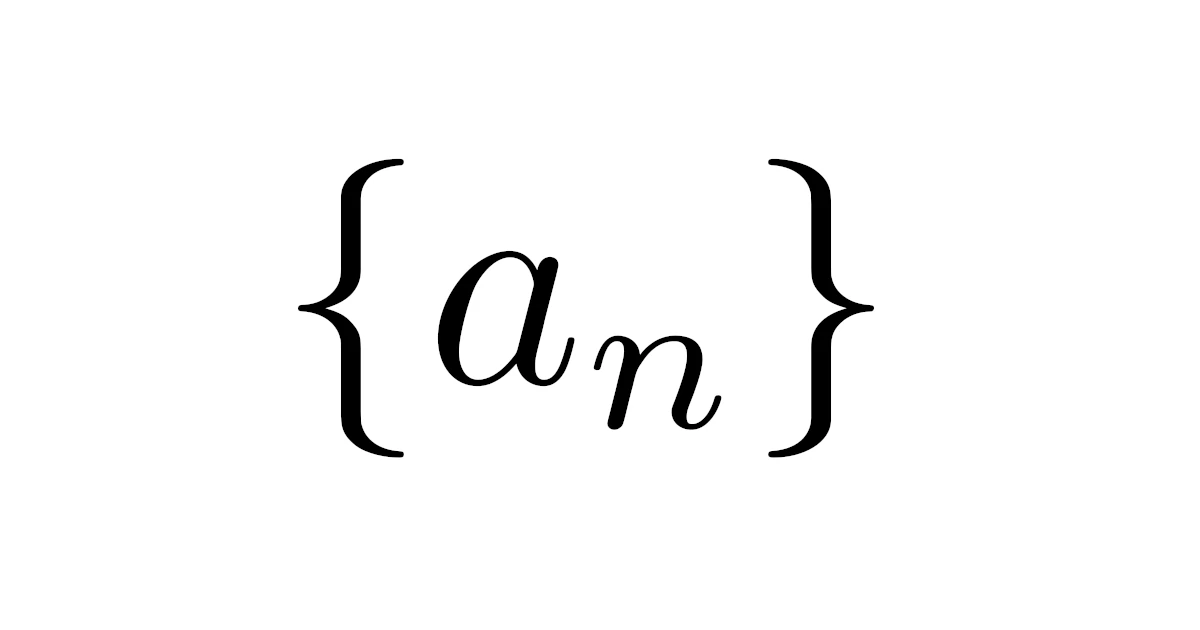
コメント