等比数列の和の公式｜例題から２パターンの使い分けを理解する

数列
2015.07.30
数列

最も基本的な数列として，等差数列・等比数列があるのでした．

これらの数列はさまざまな分かりやすい性質を持っており，初項から第$n$項までの和を求める公式もよく知られています．

等差数列の和の公式は前回の記事で説明したので，この記事では

  • 等比数列の和の公式と具体例
  • 等比数列の和の公式の導出
  • 等比数列の和の公式の補足

を順に説明します．

「数列」の一連の記事

  1. 数列の基礎
    1. 1 最初の一歩は等差数列と等比数列！
    2. 2 等差数列の和の公式を直感的に理解する方法
    3. 3 等比数列の和の公式を具体例から理解する
    4. 4 数列の和を表せるシグマ記号Σの定義と性質
    5. 5 超重要な１乗和・２乗和・３乗和の公式
    6. 6 階差数列の考え方は簡単！階差数列の公式
    7. 7 部分分数分解を用いて計算する数列の和
    8. 8 [等差×等比]型の数列の和は引き算がポイント
  1. 漸化式
    1. 9 漸化式とは？漸化式の考え方を例から解説！
    2. 10 等差数列，等比数列の漸化式
    3. 11 数学的帰納法はイメージは「ドミノ倒し」！

等比数列の和の公式と具体例

等比数列の和の公式は

  • 公比$r$が$r=1$の場合
  • 公比$r$が$r\neq1$の場合

の２種類ありますが，$r=1$の場合は簡単なので重要なのは$r\neq1$の場合です．

初項$a$，公比$r$の等比数列の初項から第$n$項までの和は

   \begin{align*}a+ar+ar^2+\dots+ar^{n-1} =\begin{cases} \dfrac{a(r^n-1)}{r-1}&(r\neq1)\\ an&(r=1) \end{cases}\end{align*}

である．

具体例から使い方を見てみましょう．

具体例１（公比$r$が$r=1$の場合）

初項３，公比１の等比数列$3,\ 3,\ 3,\ 3,\dots$の初項から第$n$項までの和を$n$で表せ．

上の公式の$a=3$, $r=1$の場合なので，

   \begin{align*}3+3+3+\dots+3=3n\end{align*}

である．

このように，公比が$1$のときは同じものを$n$個足し合わせるだけなので当たり前ですね．

具体例２（公比$r$が$r\neq1$の場合）

等比数列$3,\ 6,\ 12,\ 24,\ 38,\dots$の初項から第５０項までの和を求めよ．

等差数列$3,\ 6,\ 12,\ 24,\ 38,\dots$は初項３，公比２の等差数列だから上の公式の$a=3$, $r=2$の場合である．

よって，この数列の初項から第５０項までの和は

   \begin{align*}&\frac{3(2^{10}-1)}{2-1}=3(1024-1)=3069\end{align*}

である．

等比数列の和の公式の導出

それでは公式を導出しましょう．

公比$r$が$r=1$の場合

$r=1$のとき，数列は

   \begin{align*}a,\ a,\ a,\ a,\ \dots\end{align*}

です．よって，初項から第$n$項までの和は$a$を$n$個足すわけですから

   \begin{align*}a+a+a+\dots+a=na\end{align*}

となりますね．

公比$r$が$r\neq1$の場合

まず，和を$S_n$とおきます．つまり，

   \begin{align*}S_n=a+ar+ar^2+\dots+ar^{n-1}\end{align*}

です．両辺に$r-1$をかければ，

   \begin{align*}(r-1)S_n=(r-1)\bra{a+ar+ar^2+\dots+ar^{n-1}}\end{align*}

となります．この右辺は

   \begin{align*}&(r-1)\bra{a+ar+ar^2+\dots+ar^{n-1}} \\=&a(r-1)\bra{1+r+r^2+\dots+r^{n-1}} \\=&a\brb{(r-1)+(r^2-r)+(r^3-r^2)+\dots+(r^n-r^{n-1})} \\=&a(r^n-1)\end{align*}

と変形できるので，

   \begin{align*}(r-1)S_n=a(r^n-1)\end{align*}

が成り立ちます．両辺を$r-1$で割って，求める公式

   \begin{align*}S_n=\frac{a(r^n-1)}{r-1}\end{align*}

が得られます．

等比数列の和の公式の補足

基本が押さえられれば，以下のことにも注意できるようになると一層良いでしょう．

因数分解から$r\neq1$の場合の公式を求める

$x^2-y^2$や$x^3-y^3$が因数分解できるように，($n$乗)-($n$乗)も因数分解することができます．

実際，実数$x$, $y$と任意の自然数$n$に対し，$x^n-y^n$は

   \begin{align*}x^n-y^n=(x-y)(x^{n-1}+x^{n-2}y+x^{n-3}y^2+\dots+y^{n-1})\end{align*}

と因数分解できます．これを知っていれば，$x=r$, $y=1$を代入して

   \begin{align*}r^n-1=(r-1)(r^{n-1}+r^{n-2}+r^{n-3}+\dots+1)\end{align*}

となり，両辺に$\dfrac{a}{1-r}$をかけることで，すぐに等比数列の和の公式

   \begin{align*}\frac{r^n-1}{r-1}=a+ar+ar^2+\dots+ar^{n-1}\end{align*}

が得られます．

先ほどの導出と本質的には同じです．

公比$r$が１より大きいか小さいかで対応する

公比が$r\neq1$の場合の和は

   \begin{align*}a+ar+ar^2+\dots+ar^{n-1}=\frac{a(r^n-1)}{r-1}\end{align*}

ですが，右辺の分母と分子に$-1$をかけて

   \begin{align*}a+ar+ar^2+\dots+ar^{n-1}=\frac{a(1-r^n)}{1-r}\end{align*}

とも表せます．これらを

  • $r>1$の場合には$\dfrac{a(r^n-1)}{r-1}$
  • $r<1$の場合には$\dfrac{a(1-r^n)}{1-r}$

で使い分けると，いずれも分母は正の数となりますね．

このように，公比が１より大きいか小さいかで公式の形を使い分ければ，計算が少し見通しよくなります．

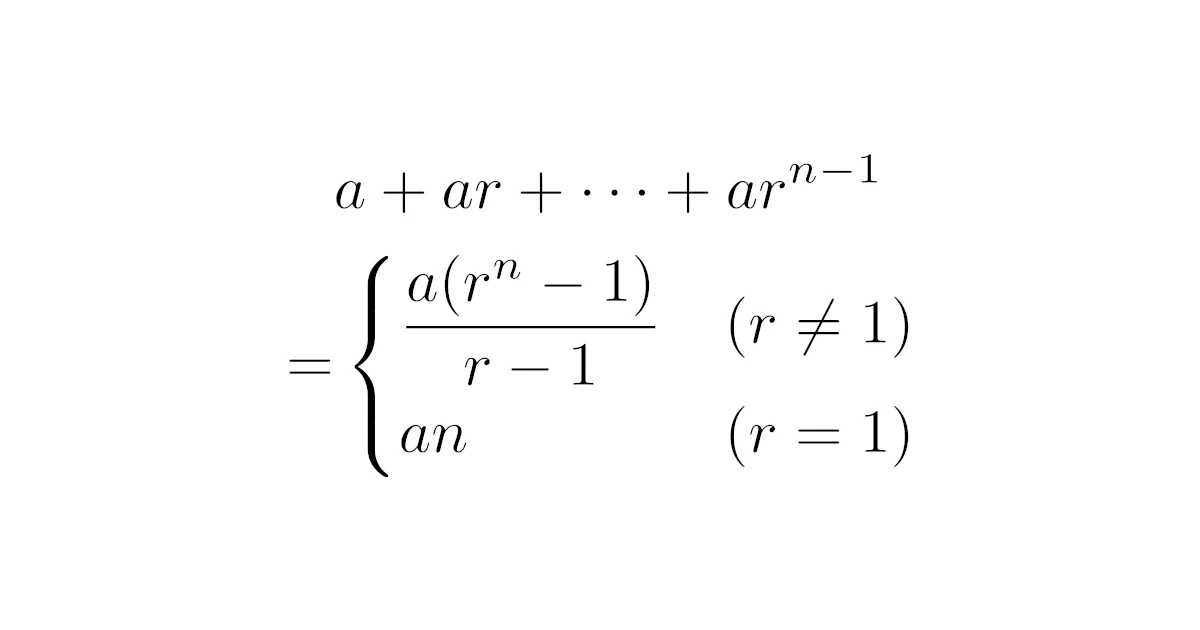
コメント