2次式の因数分解について重要なものとして
がありました.3次以上の多項式でもよく用いられる因数分解公式や定石がいくつかあります.
この記事では
- 3次式の展開・因数分解の基本の4公式
- $x^3+y^3+z^3-3xyz$の因数分解
- 偶数次のみの多項式の因数分解
- 複2次式特有の因数分解
- $x^n-y^n$と$x^n+y^n$の因数分解
を順に解説します.
「多項式」の一連の記事
3次式の展開・因数分解の基本の4公式
3次式の展開・因数分解について,次の4つの基本公式は確実に身につけてください.
実数$x$, $a$に対して,次の等式が成り立つ.
\begin{align*}&x^3+a^3=(x+a)(x^2-ax+a^2),
\\&x^3-a^3=(x-a)(x^2+ax+a^2),
\\&x^3+3ax^2+3a^2x+a^3=(x+a)^3,
\\&x^3-3ax^2+3a^2x-a^3=(x-a)^3.\end{align*}
いずれも右辺を展開することで等しいことはすぐに分かりますね.
具体例1($x^3+1$の因数分解)
公式$x^3+a^3=(x+a)(x^2-ax+a^2)$の$a=1$の場合を用いて,
\begin{align*}x^3+1&=x^3+1^3
\\&=(x+1)(x^2-x+1)\end{align*}
と因数分解できる.
具体例2($x^3-8$の因数分解)
$x$の3次式$x^3-8$を因数分解せよ.
公式$x^3-a^3=(x-a)(x^2+ax+a^2)$の$a=2$の場合を用いて,
\begin{align*}x^3-8&=x^3-2^3
\\&=(x-2)(x^2+2x+4)\end{align*}
と因数分解できる.
$x^3-8=x^3+(-2)^3$とみて,公式$x^3+a^3=(x+a)(x^2-ax+a^2)$を用いることでも因数分解できますね.
具体例3($x^3+6x^2+12x+8$の因数分解)
$x$の3次式$x^3+6x^2+12x+8$を因数分解せよ.
公式$x^3+3ax^2+3a^2x+a^3=(x+a)^3$の$a=2$の場合を用いて,
\begin{align*}x^3+6x^2+12x+8
&=x^3+3\cdot2\cdot x^2+3\cdot2^2\cdot x+2^3
\\&=(x+2)^3\end{align*}
と因数分解できる.
具体例4($x^3-9x^2+27x-27$の因数分解)
$x$の3次式$x^3-9x^2+27x-27$を因数分解せよ.
公式$x^3-3ax^2+3a^2x-a^3=(x-a)^3$の$a=3$の場合を用いて,
\begin{align*}x^3-9x^2+27x-27
&=x^3-3\cdot3\cdot x^2+3\cdot3^2\cdot x-3^3
\\&=(x-3)^3\end{align*}
と因数分解できる.
$x^3+3\cdot(-3)\cdot x^2+3\cdot(-3)^2\cdot x+(-3)^3$とみて,公式$x^3+3ax^2+3a^2x+a^3=(x+a)^3$を用いることでも因数分解できますね.
$x^3+y^3+z^3-3xyz$の因数分解
次の3変数の因数分解公式もよく問われるので知っておきたい公式です.
実数$x$, $y$, $z$に対して,次の等式が成り立つ.
\begin{align*}&x^3+y^3+z^3-3xyz
\\&=(x+y+z)(x^2+y^2+z^2-xy-yz-zx).\end{align*}
この公式も右辺を展開することで等しいことはすぐに分かりますね.
具体例5($x^3+y^3+z^3-3xyz$は非負)
$x+y+z\ge0$を満たす実数$x$, $y$, $z$に対して,$x^3+y^3+z^3-3xyz\ge 0$であることを示せ.
公式より$x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-xy-yz-zx)$だから,$x+y+z\ge0$を併せて,$x^2+y^2+z^2-xy-yz-zx\ge0$を示せばよい.
\begin{align*}&x^2+y^2+z^2-xy-yz-zx
\\&=\frac{1}{2}(2x^2+2y^2+2z^2-2xy-2yz-2zx)
\\&=\frac{1}{2}\{(x^2-2xy+y^2)+(y^2-2yz+z^2)+(z^2-2zx+x^2)\}
\\&=\frac{1}{2}\{(x-y)^2+(y-z)^2+(z-x)^2\}\ge0\end{align*}
だから,$x^3+y^3+z^3-3xyz\ge0$である.
偶数次のみの多項式の因数分解
偶数次の項のみもつ多項式は,$x^2=t$などと2乗をひとつとみることで因数分解できることがあります.
最終的には$x^2=t$とおかなくても因数分解できるくらいに慣れたいところです.
具体例6($x^4-10x^2+9$の因数分解)
$x$の4次式$x^4-10x^2+9$を因数分解せよ.
$t=x^2$とおくと,
\begin{align*}x^4-10x^2+9&=t^2-10t+9=(t-9)(t-1)
\\&=(x^2-9)(x^2-1)
\\&=(x+3)(x-3)(x+1)(x-1)\end{align*}
と因数分解できる.
具体例7($x^6-3x^4+3x^2-1$の因数分解)
$x$の6次式$x^6-3x^4+3x^2-1$を因数分解せよ.
$t=x^2$とおくと,
\begin{align*}x^6-3x^4+3x^2-1&=t^3-3t^2+3t-1=(t-1)^3
\\&=(x^2-1)^3=(x+1)^3(x-1)^3\end{align*}
と因数分解できる.
複2次式特有の因数分解
偶数次の項のみの4次式を複2次式といいます.複2次式はうまく2次の項を分けることで$X^2-Y^2$の形に持ち込んで因数分解できることがあります.
具体例8($x^4+x^2+1$の因数分解)
$x$の4次式$x^4+x^2+1$を因数分解せよ.
$t=x^2$とおき,$t^2+2t+1=(t+1)^2$に注目すると,
\begin{align*}x^4+x^2+1&=t^2+t+1=(t^2+2t+1)-t
\\&=(t^2+2t+1)-t=(t+1)^2-x^2
\\&=\{(t+1)+x\}\{(t+1)-x\}
\\&=(x^2+x+1)(x^2-x+1)\end{align*}
と因数分解できる.
具体例9($x^4-3x^2+1$の因数分解)
$x$の4次式$x^4-3x^2+1$を因数分解せよ.
$x^4-2x^2+1=(x^2-1)^2$に注目すると,
\begin{align*}x^4-3x^2+1&=(x^4-2x^2+1)-x^2=(x^2-1)^2-x^2
\\&=\{(x^2-1)+x\}\{(x^2-1)-x\}
\\&=(x^2+x-1)(x^2-x-1)\end{align*}
と因数分解できる.
具体例10($x^4-5x^2+4$の因数分解)
$x$の4次式$x^4-5x^2+4$を因数分解せよ.
$x^4-4x^2+4=(x^2-2)^2$に注目すると,
\begin{align*}x^4-5x^2+4&=(x^4-4x^2+4)-x^2=(x^2-2)^2-x^2
\\&=\{(x^2-2)+x\}\{(x^2-2)-x\}=(x^2+x-2)(x^2-x-2)\end{align*}
と因数分解できる.
$x^n-y^n$と$x^n+y^n$の因数分解
2以上の整数$n$に対して$x^n-y^n$は因数分解でき,3以上の奇数$n$に対して$x^n+y^n$は因数分解できます.
$x^n-y^n$の因数分解($n$は2以上の整数)
因数分解公式
\begin{align*}&x^2-y^2=(x-y)(x+y),
\\&x^3-y^3=(x-y)(x^2+xy+y^2)\end{align*}
から類推されるように,$x^n-y^n$($n$は2以上の整数)は次のように因数分解できます.
$n$を2以上の整数とする.実数$x$, $y$に対して,次の等式が成り立つ.
\begin{align*}x^n-y^n=(x-y)(x^{n-1}+x^{n-2}y+\dots+y^{n-1}).\end{align*}
実際に右辺を展開すれば,ほとんどの項が足し引きで消えて$x^n$と$y^n$だけが残って左辺に等しいことが分かります.
右辺を展開して
\begin{align*}&(x-y)(x^{n-1}+x^{n-2}y+\dots+y^{n-1})
\\&=x(x^{n-1}+x^{n-2}y+\dots+y^{n-1})-y(x^{n-1}+x^{n-2}y+\dots+y^{n-1})
\\&=(x^n+x^{n-1}y+\dots+xy^{n-1})-(x^{n-1}y+x^{n-2}y^2+\dots+y^n)
\\&=x^n-y^n\end{align*}
を得る.
例えば,$n=4,5$の場合には
\begin{align*}&x^4-y^4=(x-y)(x^3+x^2y+xy^2+y^3),
\\&x^5-y^5=(x-y)(x^4+x^3y+x^2y^2+xy^3+y^4)\end{align*}
となります.
$x^4-y^4$は$(x^2)^2-(y^2)^2$とみて$x^4-y^4=(x^2+y^2)(x^2-y^2)=(x^2+y^2)(x+y)(x-y)$と因数分解することもできます.
$x^n+y^n$の因数分解($n$は3以上の奇数)
因数分解公式
\begin{align*}x^3+y^3=(x+y)(x^2-xy+y^2)\end{align*}
から類推されるように,$x^n+y^n$($n$は3以上の奇数)は次のように因数分解できます.
$n$を3以上の奇数とする.実数$x$, $y$に対して,次の等式が成り立つ.
\begin{align*}x^n+y^n=(x+y)(x^{n-1}-x^{n-2}y+\dots-xy^{n-2}+y^{n-1})\end{align*}
右辺の後ろの( )の中は+の項とーの項が交互に足されますが,$n$は奇数なので最後は+の項$+y^{n-1}$になりますね.
$x^n-y^n$の因数分解と同様に,実際に右辺を展開すれば,ほとんどの項が足し引きで消えて$x^n$と$y^n$だけが残って左辺に等しいことが分かります.
右辺を展開して
\begin{align*}&(x+y)(x^{n-1}-x^{n-2}y+\dots-xy^{n-2}+y^{n-1})
\\&=x(x^{n-1}-x^{n-2}y+\dots-xy^{n-2}+y^{n-1})+y(x^{n-1}-x^{n-2}y+\dots-xy^{n-2}+y^{n-1})
\\&=(x^n-x^{n-1}y+\dots-x^2y^{n-2}+xy^{n-1})+(x^{n-1}y-x^{n-2}y^2+\dots-xy^{n-1}+y^n)
\\&=x^n+y^n\end{align*}
を得る.
例えば,$n=5$の場合には
\begin{align*}x^5+y^5=(x+y)(x^4-x^3y+x^2y^2-xy^3+y^4)\end{align*}
となります.
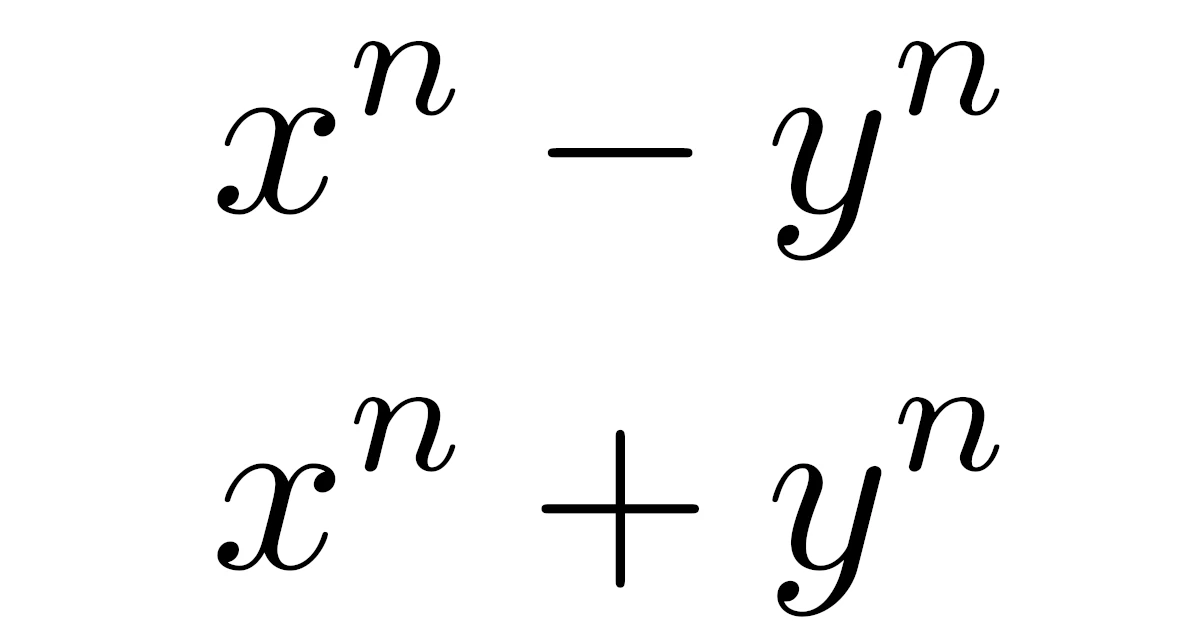
コメント