剛体の運動３｜剛体にはたらく力のつりあいとその例

物体の大きさを考えない「質点」にはたらく力がつり合っているとは単に合力が $\ve{0}$ であることをいい，例えば静止している物体にはたらく力がつり合っていれば，その物体は静止し続けるのでした．

このように，質点にはたらく力がつり合っていると，あたかも力がはたらいていないかのように質点は運動をします．

物体の大きさを考える「剛体」については，単純に力の和が0であることだけでは十分ではありません．

例えば，前回の記事で説明したように，大きさが等しく逆向きの2力があり，この2力の作用線が異なる場合には，合力は $\ve{0}$ ですが，物体は静止せず回転します．

このように，合力が $\ve{0}$ であっても物体が静止しない場合があります．

したがって，剛体の運動では回転(力のモーメント)も考える必要もあります．

一連の記事はこちら

【剛体の運動１｜物体の回転を考えるときは「力のモーメント」】
【剛体の運動２｜剛体にはたらく力の合成の４パターン】
【剛体の運動３｜剛体にはたらく力のつりあいとその例】←今の記事
【剛体の運動４｜物体の重力はドコにはたらく？重心とは！？】

【SPONSORED LINK】

1 剛体にはたらく力のつりあい
2 剛体にはたらく力のつりあいの例

剛体にはたらく力のつりあい

[剛体にはたらく力のつりあい]は，次のようになります．

[剛体にはたらく力のつりあい]　剛体にはたらく力 $\ve{F}_1,\dots,\ve{F}_n$ がつりあっているとは，次の1，2をみたすことをいう．

$\ve{F}_1+\dots+\ve{F}_n=\ve{0}$
任意の点を中心とした $\ve{F}_1,\dots,\ve{F}_n$ の力のモーメントの和が0

「力がつり合っている」と言う場合に，加わる力のベクトルの和が $\ve{0}$ であることを述べた条件1は自然ですね．

冒頭でも述べたように，質点にはたらく力のつりあいは「並進運動しない条件」である条件1だけでしたが，剛体の力のつりあいは「回転しない条件」である条件2が加わります．

剛体にはたらく力がつりあっているときには，以下が成り立ちます．

剛体にはたらく力がつりあっているとする．このとき，剛体が静止していれば静止し続け，運動していれば回転せずに等速直線運動をする．

逆に，剛体が静止していれば静止し続け，運動していれば回転せずに等速直線運動をしているとする．このとき，剛体にはたらく力はつりあっている．

このことは，質点にはたらく力のつりあいの場合と同じなので，質点の場合が分かっていればその類推で理解できますね．

【力の基本２｜力がつりあっているとどうなる？力のつりあいの例】

質点にはたらく力の合力が $\ve{0}$ のとき，それらの力はつり合っているといいます．力がつり合っているときには，あたかも力がはたらいていないかのように物体は運動します．すなわち，静止している物体は静止し続け，運動している質点は等速直線運動を続けます．

剛体にはたらく力のつりあいの例

具体例を考えます．

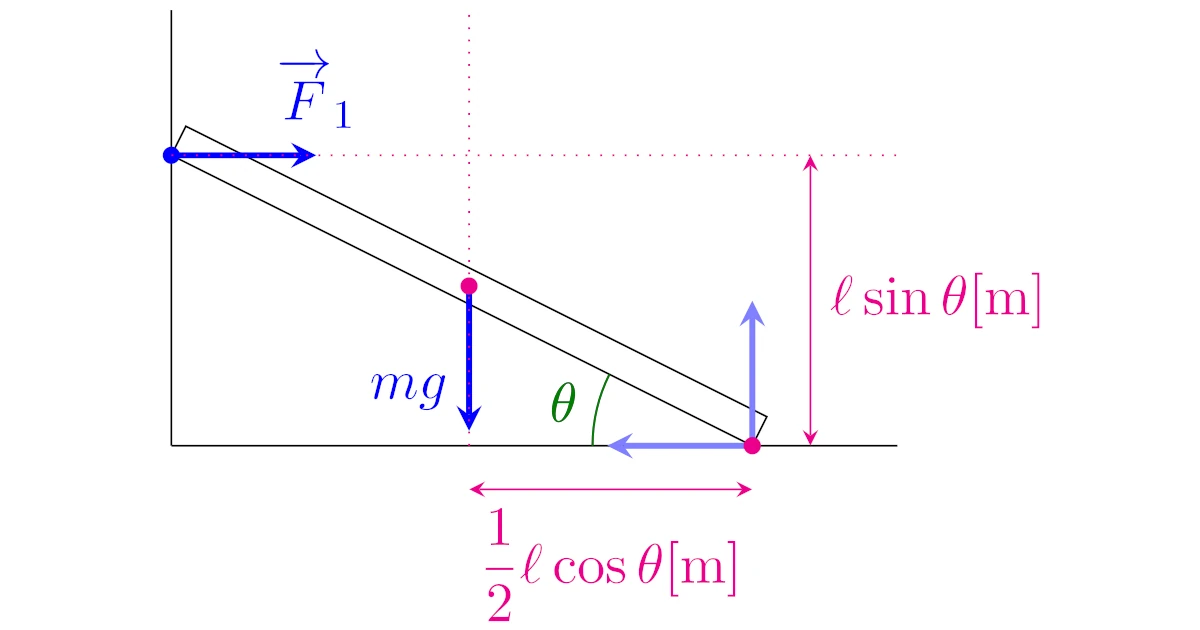
洗い床，滑らかな壁があるとし，ここに質量 $m[\mrm{kg}]$ の棒を床との角度が $\theta$ となるように壁に立てかけ，棒が静止した．このとき，

壁からの垂直抗力 $\ve{F}_1$
床と物体の摩擦力 $\ve{F}_2$
床からの垂直抗力 $\ve{F}_3$

を求めよ．ただし，重力加速度を $\ve{g}$ (大きさを $g[\mrm{m/s^2}]$ )とする．

棒は静止しているので，剛体としての棒にはたらく力はつり合っています．棒にはたらく力は

壁からの垂直抗力 $\ve{F}_1$
床と物体の摩擦力 $\ve{F}_2$
床からの垂直抗力 $\ve{F}_3$
重力 $m\ve{g}$ (大きさ $mg[\mrm{N}]$ )

ですね．ここで， $\ve{F}_1$ , $\ve{F}_2$ , $\ve{F}_3$ の大きさをそれぞれ $F_1[\mrm{N}]$ , $F_2[\mrm{N}]$ , $F_3[\mrm{N}]$ としておきましょう．

【摩擦力の基本｜摩擦力の３パターンを理解する】

摩擦力には「物体が動いていないときの摩擦力」，「物体が動かないギリギリのときの摩擦力」，「物体が動いているときの摩擦力」の3種類があります．それぞれで摩擦力の大きさがどのように表されるのかをまとめます．

合力の大きさが0

[剛体にはたらく力のつりあい]の条件1から，剛体である棒にはたらく力の合力は $\ve{0}$ になっています．すなわち，

$\begin{align*} \ve{F}_1+\ve{F}_2+\ve{F}_3+m\ve{g}=\ve{0} \end{align*}$

なので，

鉛直方向の成分
水平方向の成分

を考えると，

$\begin{align*} \begin{cases} mg=F_3\\ F_1=F_2 \end{cases} \end{align*}$

が得られます．

力のモーメントの和が0

次に，[剛体にはたらく力のつりあい]の条件2を考えます．

条件2から，どの点の周りの力のモーメントの和も0となるので，棒の接地している点の周りでの力のモーメントの和は0となっています．

まず，

$\ve{F}_2$ の作用線
$\ve{F}_3$ の作用線

はいずれも回転軸を通るので，この2本の作用線と回転軸の距離は0です．

よって， $\ve{F}_2$ と $\ve{F}_3$ の力のモーメントは0です．

ここで，棒の長さを $\ell$ とします．

このとき，

回転軸と重力 $m\ve{g}$ の作用線との距離は $\dfrac{l}{2}\ell\cos{\theta}$
回転軸と垂直抗力 $\ve{F}_1$ の作用線との距離は $\ell\sin{\theta}$

なので，

重力 $m\ve{g}$ の力のモーメントは正(反時計回り)で，大きさは $\dfrac{l}{2}mg\ell\cos{\theta}$
垂直抗力 $\ve{F}_1$ の力のモーメントは負(時計回り)で，大きさは $F_1\ell\sin{\theta}$

となりますね．

以上の全ての力のモーメントがつり合っている，すなわち和が0なので，

$\begin{align*} &0+0+\dfrac{l}{2}mg\ell\cos{\theta}-F_1\ell\sin{\theta}=0 \\\iff& mg=2F_1\tan{\theta} \end{align*}$

となります．

剛体にはたらく力のつりあい

以上から，3つの等式

$\begin{align*} \begin{cases} mg=F_3\\ F_1=F_2\\ mg=2F_1\tan{\theta} \end{cases} \end{align*}$

が得られました．これを解いて， $F_1=F_2=\dfrac{mg}{2\tan\theta}$ , $F_3=mg$ となります．よって，

$\ve{F}_1$ は水平方向の壁と逆向きに大きさ $\dfrac{mg}{2\tan\theta}$
$\ve{F}_2$ は水平方向の壁向きに大きさ $\dfrac{mg}{2\tan\theta}$
$\ve{F}_3$ は鉛直上向きに大きさ $mg$

と分かります．

なお，結果を見れば分かるように，棒の長さ $\ell[\mrm{m}]$ は全く関係がありませんね．

ですから，質量 $m[\mrm{kg}]$ と立てかける角度 $\theta$ が同じなら，長い棒であろうが短い棒であろうが $\ve{F}_1$ , $\ve{F}_2$ , $\ve{F}_3$ は変化しません．

【次の記事：剛体の運動４｜物体の重力は「重心」にはたらく！】

剛体にはたらく力を考える際には，「大きさ」と「向き」だけではなく「作用点」も大切なのでした．重力が剛体にはたらくときの作用点は重心であり，これについて例を用いて解説します．