この記事では次の問題を考えましょう.
定義域$-1\leqq x\leqq 4$の関数
\begin{align*}f(x)=\dfrac{1}{4}\bra{x^3-3x^2-2}\end{align*}
の最大値・最小値を求めよ.
微分可能な関数$f$の導関数$f’$について
- $f'(x)>0$なら単調増加
- $f'(x)<0$なら単調減少
となるのでした.
このことを利用すれば,微分可能な関数$f$の極値(極大値・極小値)を求められることを前回の記事で説明しました.
さて,関数$f$の極値は$f$の最大値・最小値の候補となる重要な値で,上の問題でもキーポイントとなります.
この記事では
- 関数の最大値・最小値の候補
- 関数の最大値・最小値の具体例
を順に説明します.
「微分法」の一連の記事
最大値,最小値の候補
そもそも関数の最大値・最小値は以下のように定義されますね.
関数$f$が$a$で最大値をとるとは,任意の$x$に対して$f(x)\leqq f(a)$となることをいう.また,関数$f$が$b$で最小値をとるとは,任意の$x$に対して$f(x)\geqq f(b)$となることをいう.
一般に$f(x)$が最大値,最小値となるような$x$の候補は
- 極値をとる$x$
- 定義域の端点$x$
- グラフが繋がっていない$x$
の3つで,この他の$x$で関数が最大値・最小値をとることはありません.
3つ目は数学IIではほぼ扱われませんが,数学IIIでは不連続点として学びます.
極値をとる点
関数の極値での値は最大値・最小値をとる点の候補です.
関数$f$が$a$で極大値をとるとは,$a$の十分近くの$x$に対して$f(x)\geqq f(a)$が成り立つことを言うのでした.
実数全体で最大であれば当然$a$の十分近くの$x$に対して$f(x)\geqq f(a)$となりますから,極大値は最大値の候補ですね.
例えば,$f(x)=-(x+1)^2+2$は$x=-1$で極大値$2$をとりますが,この極大値$2$は最大値でもありますね.
極小値についても同様に,極小値は最小値の候補ですね.
端点
関数$f$に定義域が定められているとき,定義域の「端の値」のことを端点と言い,端点は最大値,最小値をとる$x$の候補です.
例えば,$f(x)=-(x+1)^2+2$ $(-3\leqq x\leqq -2)$に対して,$y=f(x)$のグラフは下図のようになります.
よって,
- 端点$x=-2$で最大値$1$
- 端点$x=-3$で最小値$-2$
をとります.
不連続点
関数の連続性は数学IIIの範囲なので,数学IIの範囲でこの場合の最大・最小が出題されることはほとんどありません.そのため,分からない人はここを読み飛ばしても構いません.
関数$f$が$a$で不連続であるとは,大雑把に言えば「$y=f(x)$のグラフが$x=a$で切れている」ということを言い,不連続点は最大値,最小値をとる$x$の候補です.
例えば,
\begin{align*}f(x)=\begin{cases}0&(x<-1,1<x)\\x&(-1\leqq x\leqq1)\end{cases}\end{align*}
に対して,$y=f(x)$のグラフは下図のようになります.
よって,
- 不連続点$x=-1$で最小値$-1$
- 不連続点$x=1$で最大値1
をとります.
具体例
それでは具体例を考えましょう.
定義域$-1\leqq x\leqq 4$の関数
\begin{align*}f(x)=\dfrac{1}{4}\bra{x^3-3x^2-2}\end{align*}
の増減表を書き,最大値・最小値を求めよ.
関数$f(x)=\dfrac{1}{4}(x^3-3x^2-2)$の導関数$f'(x)$は
\begin{align*}f'(x)=&\dfrac{1}{4}(3x^2-6x)
\\=&\dfrac{3}{4}x(x-2)\end{align*}
なので,方程式$f'(x)=0$を解くと$x=0,2$です.また,
\begin{align*}&f(-1)=\frac{(-1)^3-3\times(-1)^2-2}{4}=-\frac{3}{2},
\\&f(0)=\frac{0^3-3\times0^2-2}{4}=-\frac{1}{2},
\\&f(2)=\frac{2^3-3\times2^2-2}{4}=-\frac{3}{2},
\\&f(4)=\frac{4^3-3\times4^2-2}{4}=\frac{7}{2}\end{align*}
なので,$-1\leqq x\leqq 4$での$f(x)$の増減表は,
\begin{align*}\begin{array}{c||c|c|c|c|c|c|c}
x & -1&\dots & 0 & \dots & 2 & \dots & 4 \\ \hline
f'(x) & &+ & 0 & – & 0 & + & \\ \hline
f(x) & -\frac{3}{2} &\nearrow & -\frac{1}{2} & \searrow & -\frac{3}{2} & \nearrow & \frac{7}{2}
\end{array}\end{align*}
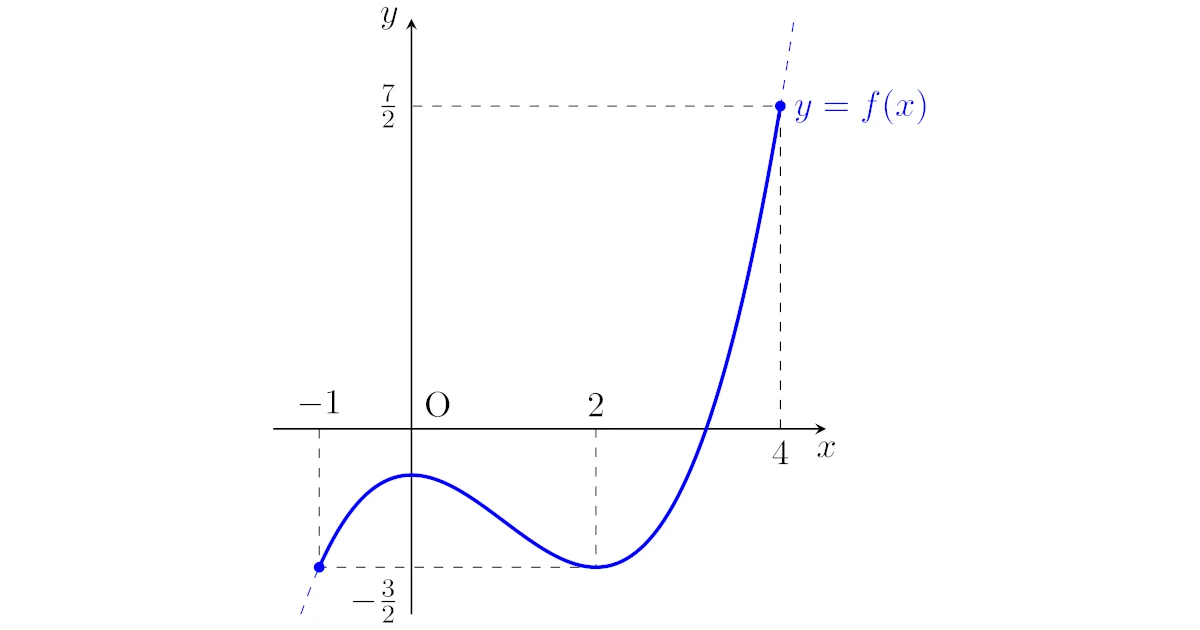
となります.増減表より$f(x)$は
- $x=4$のときに最大値$\dfrac{7}{2}$
- $x=-1,2$のときに最小値$-\dfrac{3}{2}$
をとりますね.
この例ように最大値・最小値をとる$x$が2つ以上ある場合もあります.
コメント