 場合の数と確率
場合の数と確率 組み合わせの場合の数ₙCₖ|考え方・求め方・基本性質を攻略
「6個の文字A, B, C, D, E, Fから3つ選ぶ場合の数」のように,いくつかのものからいくつかを選ぶことを「組み合わせ」と言い,場合の和では基本中の基本です.この記事では,組み合わせの場合の数の考え方と求め方を説明します.
 場合の数と確率
場合の数と確率 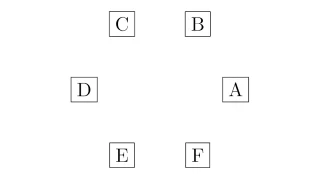 場合の数と確率
場合の数と確率  場合の数と確率
場合の数と確率 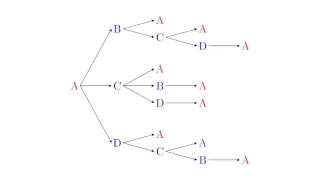 場合の数と確率
場合の数と確率  ワンポイント数学
ワンポイント数学  ワンポイント数学
ワンポイント数学 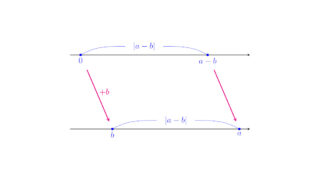 ワンポイント数学
ワンポイント数学 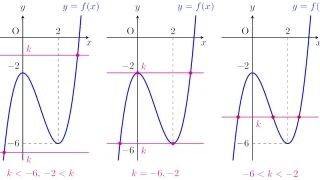 微分法
微分法 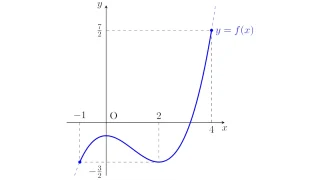 微分法
微分法 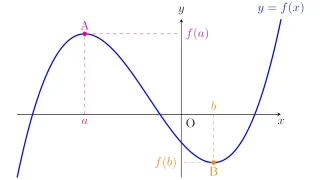 微分法
微分法