$xy$平面上で考える距離については
- 2点間の距離
- 点と直線の距離
の2つが重要です.
2点間の距離は中学校でも習うように,三平方の定理が分かっていれば簡単に導けますが,一方の点と直線の距離の少し複雑で苦手意識のある人も少なくないようです.
この記事では,この2種類の距離
- 2点間の距離
- 点と直線の距離
を順に説明します.
「図形と方程式」の一連の記事
2点間の距離
$xy$平面上の2点の距離は次のように求められます.
$xy$平面上の2点$\mrm{A}(x_1,y_1)$, $\mrm{B}(x_2,y_2)$間の距離$\mrm{AB}$は次で得られる.
\begin{align*}\mrm{AB}=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\end{align*}
ベースにあるのは三平方の定理ですね.
$x_1\neq x_2$かつ$y_1\neq y_2$のとき,点$\mrm{C}(x_1,y_2)$をとると,$\tri{ABC}$は
\begin{align*}\mrm{AC}=|y_2-y_1|,\quad
\mrm{BC}=|x_2-x_1|,\quad
\ang{ACB}=90^{\circ}\end{align*}
を満たす.
よって,$\tri{ABC}$について三平方の定理より,
\begin{align*}\mrm{AB}
=&\sqrt{\mrm{BC}^2+\mrm{CA}^2}
\\=&\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\end{align*}
を得る.
また,$y_1=y_2$のときは
\begin{align*}\mrm{AB}
=&|x_2-x_1|
=\sqrt{(x_1-x_2)^2}
\\=&\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\end{align*}
となって成り立ち,$x_1=x_2$のときは
\begin{align*}\mrm{AB}
=&|y_2-y_1|
=\sqrt{(y_1-y_2)^2}
\\=&\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\end{align*}
となって成り立つ.
[2], [3]の場合は「潰れた直角三角形」を考えていると思えば[1]と同じですね.
なお,途中では$\sqrt{a^2}=|a|$であることを用いています.$\sqrt{a^2}=a$は間違いなので注意して下さい.
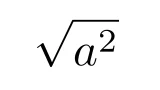
平方根と根号√の基本・二重根号の外し方
点と直線の距離
それでは点と直線の距離の説明に移ります.
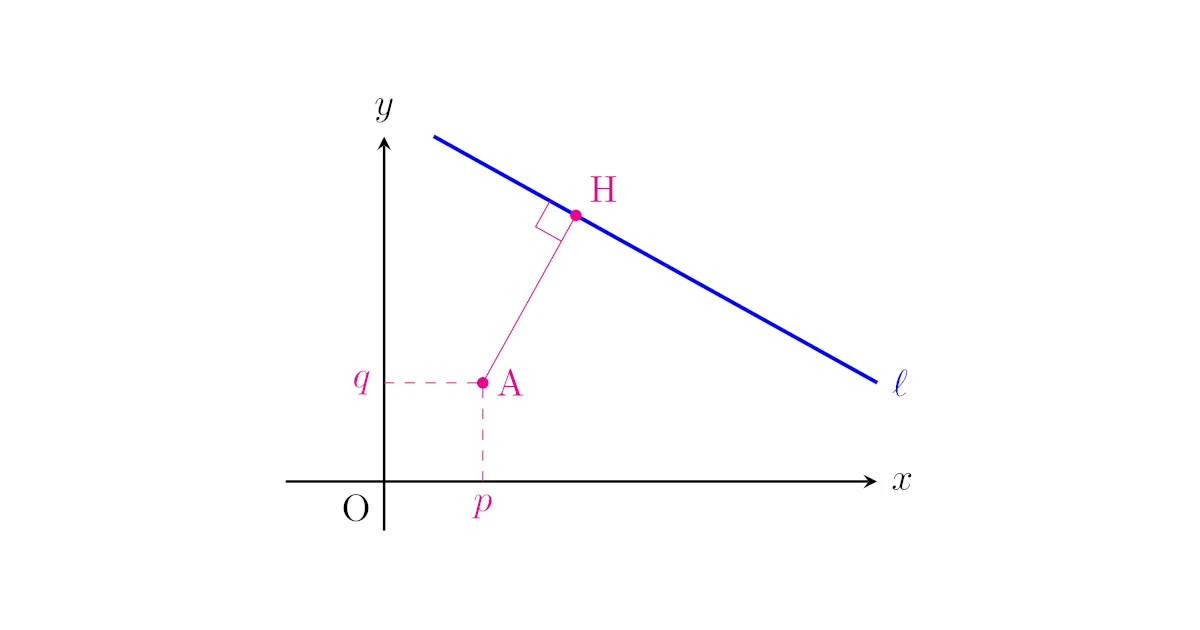
点$\mrm{A}$と直線$\ell$に対して,点$\mrm{A}$を通り直線$\ell$に垂直な直線と直線$\ell$の交点$\mrm{H}$をとる.
このとき,線分$\mrm{AH}$の長さを点$\mrm{A}$と直線$\ell$の距離という.
この定義で点$\mrm{H}$を点$\mrm{A}$から直線$\ell$に下ろした垂線の足といいます.
点と直線の距離の定義には座標が使われていないので,座標上でなくても考えることができますね.
垂線の足との距離を「点と直線の距離」という名前は,次が成り立つことに由来します.
点$\mrm{A}$と直線$\ell$に対して,点$\mrm{A}$と直線$\ell$上の点$\mrm{X}$をとる.このとき,線分$\mrm{AX}$の長さの最小値は点$\mrm{A}$と直線$\ell$の距離に等しい.
要するに,点$\mrm{X}$を直線$\ell$上を動かして点$\mrm{A}$に最も近付くのが$\mrm{X}$が点$\mrm{A}$から直線$\ell$に下ろした垂線の足に一致するときで,その長さが点と直線の距離ということですね.
点$\mrm{A}$から直線$\ell$に下ろした垂線の足を$\mrm{H}$とする.
このとき,$\mrm{H}\neq\mrm{X}$なら$\tri{ABH}$は$\ang{B}=90^\circ$の直角三角形だから,三平方の定理より
\begin{align*}\mrm{AX}^2
=\mrm{AH}^2+\mrm{XH}^2
>\mrm{AH}^2\end{align*}
なので,$\mrm{AX}>0$, $\mrm{AH}>0$より$\mrm{AX}>\mrm{AH}$が成り立つ.
また,$\mrm{H}=\mrm{X}$なら$\mrm{AX}=\mrm{AH}$が成り立つから,線分$\mrm{AX}$の長さの最小値は点$\mrm{A}$と直線$\ell$の距離に等しい.
点と直線の距離の公式
$xy$平面において
- 点$\mrm{A}$の座標
- 直線$\ell$の方程式
が分かっている場合,次のように点と直線の距離を求めることができます.
$xy$平面上の点$\mrm{A}(p,q)$と直線$\ell:ax+by+c=0$の距離$d$は次で得られる.
\begin{align*}d=\frac{|ap+bq+c|}{\sqrt{a^2+b^2}}\end{align*}
形としては
- 分子は直線の方程式$ax+by+c=0$に点の座標$(p,q)$を代入した値の絶対値
- 分母は$\sqrt{(\text{$x$の係数})^2+(\text{$y$の係数})^2}$
となっていますね.
具体例
証明は後回しにして,先に具体例から使い方を見てみましょう.
直線$2x+3y-6=0$と点$(4,3)$の距離$d$を求めよ.
点と直線の距離の公式において,$(a,b,c)=(2,3,-6)$, $(p,q)=(4,3)$の場合に相当するので,
\begin{align*}
\frac{|2\times5+3\times1-4|}{\sqrt{2^2+3^2}}
=\frac{9}{\sqrt{13}}
\bra{=\frac{9}{13}\sqrt{13}}
\end{align*}
が求める距離となりますね.
証明
それでは証明しましょう.
点$\mrm{A}$から直線$\ell$に下した垂線の足を点$\mrm{H}$とする.このとき,$d=\mrm{AH}$である.
直線$\mrm{AH}$は点$\mrm{A}(p,q)$を通り,直線$\ell:ax+by+c=0$に垂直だから,一般の直線の方程式の垂直条件より直線$\mrm{AH}$の方程式は,
\begin{align*}&b(x-p)-a(y-q)=0
\\\iff& bx-ay-bp+aq=0\end{align*}
である.よって,直線$\ell$の方程式と直線$\mrm{AH}$の方程式の連立方程式
\begin{align*}\begin{cases}
ax+by+c=0\\
bx-ay-bp+aq=0
\end{cases}\end{align*}
を解けば,点$\mrm{H}$の座標が得られる.
第1式の両辺を$a$倍,第2式の両辺を$b$倍して足し合わせると,
\begin{align*}
&a(ax+by+c)+b(bx-ay-bp+aq)=0
\\\iff& x=\frac{b^2p-abq-ac}{a^2+b^2}
\end{align*}
であり,これを連立方程式の第1式に代入して
\begin{align*}
&\frac{ab^2p-a^2bq-a^2c}{a^2+b^2}+by+c=0
\\\iff& y=\frac{a^2q-abp-bc}{a^2+b^2}
\end{align*}
となるから,点$\mrm{H}$の座標は,
\begin{align*}\bra{\frac{b^2p-abq-ac}{a^2+b^2},\frac{a^2q-abp-bc}{a^2+b^2}}\end{align*}
である.よって,
\begin{align*}d=&\mrm{AH}
\\=&\sqrt{\bra{\frac{b^2p-abq-ac}{a^2+b^2}-p}^2+\bra{\frac{a^2q-abp-bc}{a^2+b^2}-q}^2}
\\=&\sqrt{\bra{\frac{-a^2p-abq-ac}{a^2+b^2}}^2+\bra{\frac{-b^2q-abp-bc}{a^2+b^2}}^2}
\\=&\sqrt{\brb{\frac{a(ap+bq+c)}{a^2+b^2}}^2+\brb{\frac{b(bq+ap+c)}{a^2+b^2}}^2}
\\=&\sqrt{\frac{(a^2+b^2)(ap+bq+c)^2}{(a^2+b^2)^2}}
\\=&\sqrt{\frac{(ap+bq+c)^2}{a^2+b^2}}
=\frac{|ap+bq+c|}{\sqrt{a^2+b^2}}\end{align*}
となって,点と直線の距離の公式を得る.
コメント