高校数学で学ぶ重要な証明方法である背理法は
「『$X$が成り立たない』と仮定して矛盾を導くことができれば,この仮定は誤りで『$X$が成り立つ』ことが分かる」
という論法のことをいうのでした.
「$X$が成り立たない」という嘘を暴きたければ,その嘘と矛盾することを示せばいいという考え方が背理法なわけですね.
ただ背理法の考え方に加えて,どのような証明で背理法が有効なのかが分かっていないと実際の問題で背理法を思いつくのは難しいかもしれません.
そこで,この記事では
- 背理法が有効な証明問題の特徴
- 背理法を用いる他の証明問題の具体例
を順に説明します.
背理法が有効な証明の特徴
背理法が有効な証明問題は「証明したいことを否定すると扱いやすくなる」というタイプの問題です.その具体例としてよくあるのは
- 否定の証明
- 「少なくとも〜」の証明
です.もちろんこれら以外でも背理法が有効な証明問題もありますが,これら2つタイプの証明で背理法が有効なことはとても多いので,しっかり意識しておきましょう.
実際,前回の記事では以下の問題を証明しました.
$\sqrt{2}$は無理数であることを示せ.
そもそも無理数の定義が「有理数でない実数」でしたから,この問題は「$\sqrt{2}$は有理数でないことを示せ」と否定の証明になっているわけですね.
無理数であることを証明する際に背理法を用いると証明しやすいことが多いのはこれが理由です.
背理法の具体例
それでは具体的に背理法が有効な証明問題を考えましょう.
次の問いに答えよ.
- 実数$x$, $y$, $z$が$xyz=0$を満たすとき,$x$, $y$, $z$の少なくとも1つは$0$であることを示せ.
- 実数$x$, $y$が$x+y>0$を満たすとき,$x>0$または$y>0$が成り立つことを示せ.
- 整数$a$, $b$は等式$a^2+2=4b$を満たし得ないことを示せ.
- $a$, $b$が無理数なら,$a+b$と$a-b$の少なくとも一方は無理数であることを示せ.
- 素数が無限に存在することを示せ.
- $\tan{1^\circ}$は有理数か(2006 京大).
例1(積が0となる実数)
実数$x$, $y$, $z$が$xyz=0$を満たすとき,$x$, $y$, $z$の少なくとも1つは0であることを示せ.
「『少なくとも〜』の証明」なので背理法を真っ先に思いつきたいところです.
背理法により示す.すなわち,「$x$, $y$, $z$の少なくとも1つは0」の否定「$x$, $y$, $z$はいずれも0でない」が成り立つと仮定して矛盾を導く.
この仮定より$xyz\neq0$だから,$xyz=0$に矛盾する.
よって,仮定が誤りなので「$x$, $y$, $z$の少なくとも1つは0」が成り立つ.
例2(和が正となる実数)
実数$x$, $y$が$x+y>0$を満たすとき,$x>0$または$y>0$が成り立つことを示せ.
「$x>0$または$y>0$が成り立つ」は「$x>0$と$y>0$の少なくとも一方が成り立つ」ということなので,「『少なくとも〜』の証明」になっています.
背理法により示す.すなわち,「$x>0$または$y>0$」の否定「$x\le0$かつ$y\le0$」が成り立つと仮定して矛盾を導く.
この仮定より$x+y\le0+0=0$だから,$x+y>0$に矛盾する.
よって,仮定「$x\le0$かつ$y\le0$」が誤りなので,「$x>0$または$y>0$」が成り立つ.
なお,この問題の対偶を用いた証明は以下の記事を参照してください.
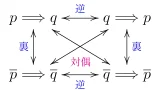
例3(整数の等式)
整数$a$, $b$は等式$a^2-2=4b$を満たし得ないことを示せ.
「否定の証明」なので背理法が真っ先に思い付きたいところです.
背理法により示す.すなわち,「整数$a$, $b$が等式$a^2-2=4b$を満たす」と仮定して矛盾を導く.
この仮定より$a^2=2(1+2b)$なので$a^2$は偶数だから,$a$も偶数となる.
よって,$a=2k$($k$は整数)とおけるから,$a^2=2(1+2b)$に代入して
となる.しかし,左辺$2k^2$は偶数,右辺$1+2b$は奇数だから矛盾する.
よって,仮定が誤りなので整数$a$, $b$は等式$a^2-2=4b$を満たし得ない.
例4(無理数の和と差)
$a$, $b$が無理数なら,$a+b$と$a-b$の少なくとも一方は無理数であることを示せ.
「『少なくとも〜』の証明」であり「否定の証明」でもありますね.
$a+b$と$a-b$がいずれも有理数であると仮定して矛盾を導く.
この仮定から$a+b=\dfrac{q}{p}$($p$, $q$は整数,$p\neq0$),$a+b=\dfrac{s}{r}$ ($r$, $s$は整数,$r\neq0$)とおける.
2式の辺々を加えたものと引いたものはそれぞれ
である.$2pr$, $qr+ps$, $qr-ps$はいずれも整数だから$a$, $b$はともに有理数である.
よって矛盾するから,$a+b$と$a-b$の少なくとも一方は無理数である.
例5(素数は無限に存在する)
素数が無限に存在することを示せ.
「無限」の定義が「有限でない」なので「否定の証明」と考えられます.
「無理数」の定義が「有理数でない」であるのと似た感覚ですね.
素数が有限個$a_1,\dots,a_n$しかないと仮定して矛盾を導く.
このとき,任意の$i=1,\dots,n$に対して
であり,$a_i\ge2$より$\dfrac{1}{a_i}$は整数でないので,$\dfrac{x}{a_i}$も整数でない.
よって,$x$は$a_i$で割り切れないから,$x$は自身と1でしか割り切れないことになり素数である.
一方,$x>a_1$だから$a_1,\dots,a_n$のいずれとも異なり,$a_1,\dots,a_n$が全ての素数としたことに矛盾する.
よって,素数は無限に存在する.
例6($\tan{1^\circ}$は有理数か?)
$\tan{1^\circ}$は有理数か(2006 京大).
(6)は少し三角関数に慣れていれば$\tan{1^\circ}$が無理数になりそうだという直感がはたらくかと思います.
とするなら,「無理数」は「有理数でない」でしたから「否定の証明」となりますね.
$\tan{1^\circ}$が有理数であると仮定して矛盾を導く.
このとき,$\tan$の加法定理より$\tan{(1^\circ+n^\circ)}=\dfrac{\tan{1^\circ}+\tan{n^\circ}}{1-\tan{1^\circ}\tan{n^\circ}}$が成り立つ.
$\tan{n^\circ}$が有理数なら,右辺は有理数だから$\tan{(1^\circ+n^\circ)}$も有理数である.
また,仮定より$\tan{1^\circ}$は有理数だから,数学的帰納法により任意の自然数$n$に対して$\tan{n^\circ}$は有理数である.
一方,$\tan{30^\circ}=\dfrac{1}{\sqrt{3}}$は無理数なので,矛盾する.よって,$\tan{1^\circ}$は無理数である.
いまの解答では省略しましたが,実際の入試では$\dfrac{1}{\sqrt{3}}$が無理数であることも証明しておくのが無難です.
「$\dfrac{1}{\sqrt{3}}$が無理数であること」の証明は「$\sqrt{2}$が無理数であること」の証明と同様に示すことができるので,前回の記事を参照してください.
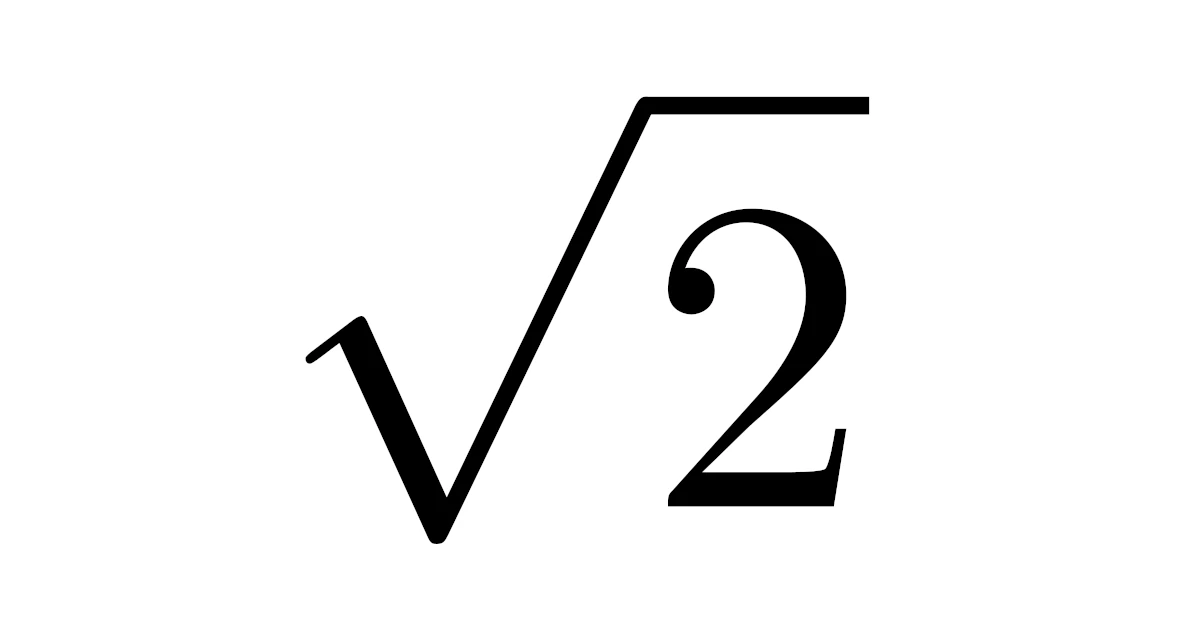
コメント