前回の記事では関数$f$の導関数$f’$が
で定義されることを説明し,具体的にいくつか導関数を求めました.そこで,次の問題を考えましょう.
関数$f(x)=x^{4}-3x^{2}+5$を微分せよ.
導関数$f’$の定義に従って解くなら
を計算することになりますが,この計算は少し面倒そうです.
実は多項式の導関数は簡単に求める公式が知られており,その公式を用いると定義に従って計算しなくても導関数が求まります.
この記事では,
- $f(x)=x^n$の導関数
- 定数倍・和の導関数
- 多項式の導関数
を順に説明します.
「微分法」の一連の記事
$f(x)=x^n$の導関数
関数$f(x)=x^n$の導関数は次のようになります.
公式
これはとても重要なので当たり前に言えるようにしてください.
$0$以上の整数$n$に対し,$f(x)=x^{n}$の導関数は
である.ただし,$n=0$のときは$f(x)=1$で$f'(x)=0$,$n=1$のときは$f(x)=x$で$f'(x)=1$である.
証明は
- $n=0$のとき
- $n=1$のとき
- $n\geqq2$のとき
に分けて行いましょう.
[$n=0$のとき] $f(x)=1$なので
が成り立つ.
[$n=1$のとき] $f(x)=x$なので
が成り立つ.
[$n\geqq2$のとき] 二項定理より
だから,
が従う.
$n\geqq2$のときに用いた二項定理について詳しくは,以下の記事を参照してください.
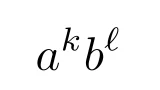
導関数のもうひとつの定義式$f'(x)=\lim\limits_{b\to x}\dfrac{f(x)-f(b)}{x-b}$からも導くことができます.
具体例
例えば,次のようになりますね.
関数$f(x)=x^3$を微分せよ.
上の公式で$n=3$の場合に相当するから,
である.
形式的には$x^n$の指数部分$n$が$-1$され,$n$が係数に降りてくるというわけですね.
定数倍・和の導関数
導関数をもつ関数の定数倍・和については,次の定理が基本的です.
[定数倍・和の導関数] 定数$k$と導関数をもつ関数$f$, $g$に対して,
が成り立つ.
言葉で説明すると
- 関数の定数倍は微分に関係しない
- 和の導関数$(f+g)’$は導関数の和$f’+g’$に等しい
が成り立つというわけですね.
導関数の定義より
だから,$(kf)’=kf’$が成り立つ.また,やはり導関数の定義より
だから,$(f+g)’=f’+g’$が成り立つ.
この2つの等式をまとめて,次のようにいうこともできます.
[定数倍・和の導関数2] 定数$k$, $\ell$と導関数をもつ関数$f$, $g$に対して,
が成り立つ.
いま示した定理より
が成り立つ.
[定数倍・和の導関数2]で,$\ell=0$とすると$(kf)’=kf’$が成り立ち,$k=\ell=1$とすると$(f+g)’=f’+g’$が成り立つので,[定数倍・和の導関数2]は[定数倍・和の導関数]のそれぞれの公式の拡張になっているということもできますね.
多項式の導関数
以上を踏まえて多項式の導関数を考えましょう.
[定数倍・和の導関数2]で微分をバラバラにしてから,$f(x)=x^{n}$の導関数の公式で各項を微分すれば多項式を微分することができます.
具体例1
関数$f(x)=x^{3}-x^{2}$を微分せよ.
[定数倍・和の導関数2]の公式と$f(x)=x^{n}$の導関数の公式より
である.
具体例2
関数$f(x)=2x^{4}-3x^{2}+5$を微分せよ.
[定数倍・和の導関数2]の公式と$f(x)=x^{n}$の導関数の公式より
である.
この多項式は3項からなりますが,一般に
と1歩ずつ考えれば,全部バラバラにできることが分かりますね.
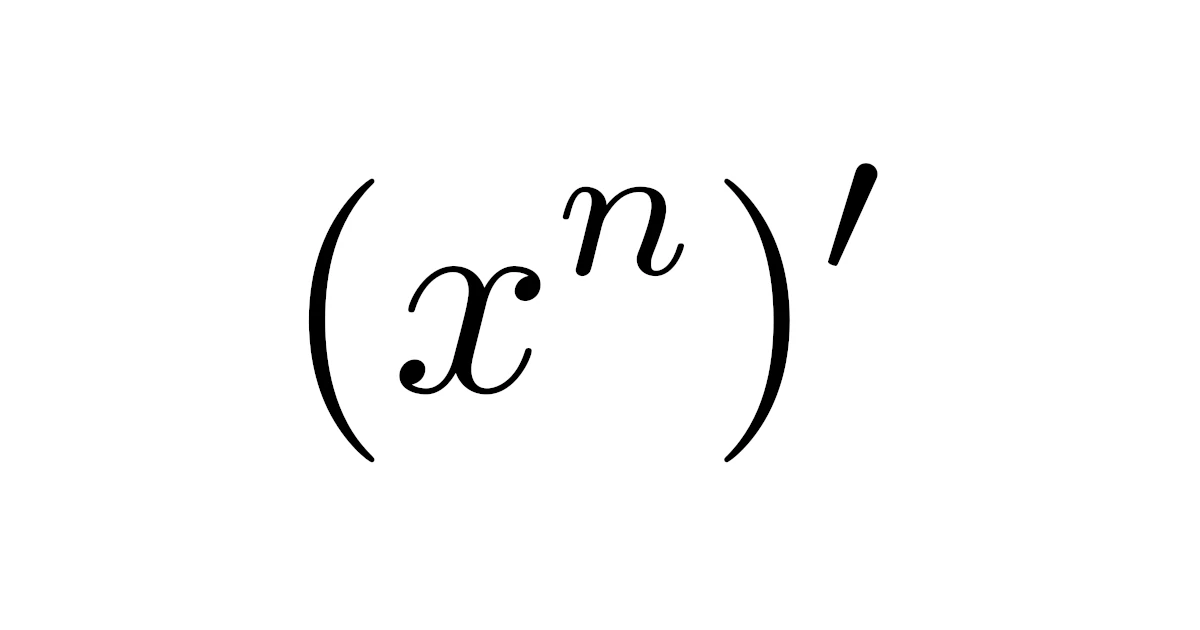
コメント