この記事では次の問題を考えます.
等式$1=0.999\dots$は成り立つか?
この話題を初めて考えた人は「いやいや,どう見ても成り立たんやろ」「成り立ちそう」「うーむ,分からぬ……」と様々な考えが浮かぶと思います.
結論から言えば,実は$1=0.999\dots$は数学的に正しいことが証明できます.
人によっては「いやいや,そんなことないやろ!」と受け入れ難い人もいるかもしれませんね.
この記事では
- 怪しい証明
- それっぽい証明
- 無限級数による説明
- 無限小数の定義
詳しくは無限級数の知識を使うことで$1=0.999\dots$が導けるのですが,途中までは無限級数の知識がなくても成り立ちそうだと思えるように説明しています.
怪しい証明
まずは怪しい証明ですが,「成り立ちそう」ということを実感してもらうために1つ書いてみます.
[怪しい証明]例えば,
\begin{align*}&1-0.9=0.1,\\&1-0.99=0.01,\\&1-0.999=0.001\end{align*}
である.同様に,小数第$n$位まで9が続く実数$0.999\dots9$と$1$の差は
\begin{align*}1-0.999\dots9=0.00\dots01\end{align*}
と$0.00\dots01$は小数第$n$位に初めて1が現れる.
いま,$0.999\dots$は9が無限に続くので,$1-0.999\dots$は0が無限に続く,つまり0となる.
よって,$1=0.999\dots$である.
おお!怪しい!ものすごく怪しい!
ですが,$1=0.999\dots$が正しいと主張する気持ちを少しは分かって頂けたのではないかと思います.
それっぽい証明
次に「それっぽい証明」を2つしてみます.
それっぽい証明1
[それっぽい証明1]$\dfrac{1}{3}=0.333\dots$である.
左辺を3倍すると$3\times\dfrac{1}{3}=1$であり,右辺を3倍すると$3\times0.333\dots=0.999\dots$である.
よって,$1=0.999\dots$を得る.
ううむ,確かにそれっぽい.しかし,煙に巻かれたような気もします.
なんとなく$3\times0.333\dots=0.999\dots$が怪しいですね.無限小数に3をかけているのが少し気持ち悪い.
そこまで考えると$\dfrac{1}{3}=0.333\dots$が本当に正しいのかも,ちゃんと証明しなければならない気持ちにもなってきます.
同じくつぎの「証明」もそれっぽいですが,やはり少し気持ち悪いです.
それっぽい証明2
[それっぽい証明2]$x=0.999\dots$とおく.両辺を10倍すると$10x=9.999\dots$である.これから$x=0.999\dots$を引くと,\begin{align*}\begin{matrix}&10x&=&9.999\dots\\-)&x&=&0.999\dots\\\hline&10x-x&=&9\end{matrix}\end{align*}
と分かる.
こうして得られた方程式$10x-x=9$を解くと$x=1$となる.もとより$x=0.999\dots$だったので,$1=0.999\dots$を得る.
ううむ,これもそれっぽいですが,やはり煙に巻かれた感がありますね.
その原因はやはり無限小数を$10$倍していたり,無限小数から無限小数を引いているあたりでしょう.
しかし,「それっぽい説明1」よりは,少し数学的になった気はします.
無限級数による説明
さて,ここからきちんと数学の話になってきます.
ここまで読まれた方は「$0.999\dots$の$\dots$の正体が分かっていないのが,なんかモヤモヤしている原因だなあ」という気になってきたと思います.なってきたことにしてください.
では,数学的に”$0.999\dots$”がどういうことなのかを説明します.
ここで,一番最初にした[怪しい説明]が生きてきます.
たとえば,$0.1=10^{-1}$, $0.01=10^{-2}$, $0.001=10^{-3}$のように,$0.000\dots01$と$n$個並ぶものは$10^{-n}$と表せることを思い出してください.
これを使って$0.9$, $0.99$, $0.999$を各桁について数を分解すると,
\begin{align*}&0.9=9\times10^{-1},
\\&0.99=9\times10^{-1}+9\times10^{-2},
\\&0.999=9\times10^{-1}+9\times10^{-2}+9\times10^{-3}\end{align*}
となります.これは
\begin{align*}&0.9=\sum_{k=1}^{1}9\times10^{-k},
\\&0.99=\sum_{k=1}^{2}9\times10^{-k},
\\&0.999=\sum_{k=1}^{3}9\times10^{-k}\end{align*}
と表せますね.
これをずっと続けていくと,
\begin{align*}\sum_{k=1}^{n}9\times10^{-k}=0.999\dots9\end{align*}
となります.これは等比数列の無限級数
\begin{align*}\sum_{k=1}^{\infty}9\times10^{-k}\end{align*}
の部分和です.どうでしょう.見えてきましたか?
無限小数とは
ここで,「なんだか$0.999\dots$は無限級数$\displaystyle\sum_{k=1}^{\infty}9\times10^{-k}$に等しそうだなあ」という気持ちになります.
${0.999\dots}$の定義
しかし,この書き方だと「$0.999\dots$があって,それが$\displaystyle\sum_{k=1}^{\infty}9\times10^{-k}$に等しい」ということですが,まだ無限小数$0.999\dots$をきちんと定義していないので,なんとも言えません.
では,どうするか.
実は「$0.999\dots$を$\displaystyle\sum_{k=1}^{\infty}9\times10^{-k}$で定義」してしまうのです.
無限級数は数学IIIの範囲ですが,数学IIIを履修していなくてもこのずっと続く気持ちは理解して頂けると思います.
小学校では「$0.333\dots$ってずっと続く小数は無限小数って言うんやで!」と習いますが,本当は数IIIで無限級数を習って初めて厳密に定義できるのです.
さて,$0.999\dots=\displaystyle\sum_{k=1}^{\infty}9\times10^{-k}$で定義したわけですが,右辺は無限等比級数ですから(数学IIIで学ぶように)計算ができます.
いま,数列$\{a_n\}$は一般項が$a_n=9\times10^{-n}$の等比数列で,この初項は$a_1=0.9$で公比$r=10^{-1}$は$-1<r<1$をみたすので,無限等比級数$\displaystyle\sum_{k=1}^{\infty}9\times10^{-k}$は
\begin{align*}\sum_{k=1}^{\infty}9\times10^{-k}=\dfrac{0.9}{1-10^{-1}}=\dfrac{0.9}{1-0.1}=\dfrac{0.9}{0.9}=1\end{align*}
と計算されます!
おお!たしかに$1=0.999\dots$となりましたね!
無限小数の定義
一般に無限小数は次のように定義されます.
各項が0から9までのいずれかの整数をとる数列を$\{a_n\}$とする.このとき,無限級数
\begin{align*}\sum_{k=1}^{\infty}a_{k}\times10^{-k}\end{align*}
で定まる実数を$0.a_1a_2a_3\dots$と表し,この実数の表し方を十進小数表示という.
任意の正の整数$n$に対して$a_{n’}\neq0$となるような$n$より大きい整数$n’$が存在するとき,$0.a_1a_2a_3\dots$を無限小数という.
後半の「任意の正の整数$n$に対して$a_{n’}\neq0$となるような$n$より大きい整数$n’$が存在する」とは,「小数点以下どこまでいっても必ず0以外の数が現れる」ということを言っています.
いままで何気なく使ってきた無限小数が,実は無限級数で定義されるということが理解できたでしょうか?
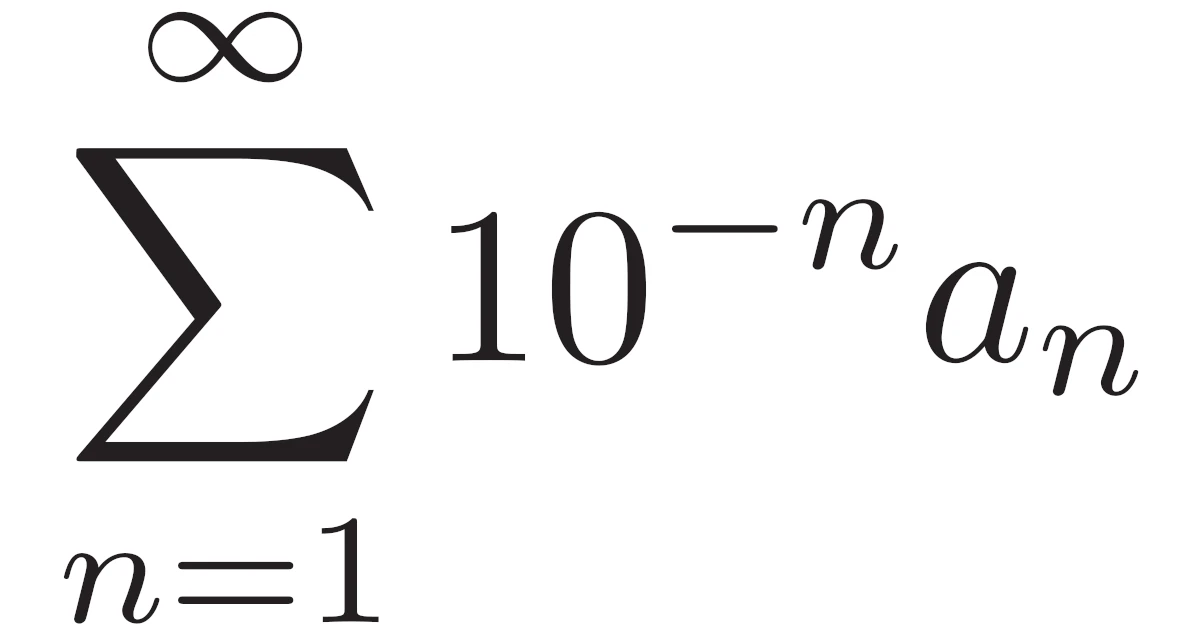
コメント