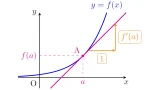
微分不可能な関数の例は？｜微分可能性の直感的な理解

関数$f(x)$を微分して導関数$f'(x)$を考えることにより，$xy$平面上のグラフ$y=f(x)$の接線の傾きを考えることができるのでした．

また，これにより関数$f(x)$の増減を考えることもできますね．

このように，微分法は関数の増減を調べるためにとても便利ですが，関数はいつでも微分可能であるとは限りません．

「微分可能でないこと」を「微分不可能」と言いますが，高校数学では微分不可能であるような関数を扱うことは多くありません．

とはいえ，数学IIIでは微分の考え方をある程度扱う以上，微分不可能であるような例も知っておくとより理解が深まります．

この記事では，微分不可能な関数について考えます．

関数$f(x)$に対して，$y=f(x)$のグラフの接線を求めるには，微分係数を用いることになります．微分係数は極限で定義されますが，その本質は平均変化率の極限です．微分係数の求め方が図形的にイメージできていれば，２度と定義式を忘れることはありません．

【微分法４｜y=f(x)のグラフの描き方は４ステップでOK】

$y=f(x)$のグラフの概形を調べるためには，関数$f(x)$の増減を見るのが最も素朴な方法でしょう．増加していれば右上がりの概形に，減少していれば右下がりの概形になります．関数$f(x)$の増減は$y=f(x)$のグラフの接線の傾きを見ることで理解することができ，そのために微分法を用います．

1 微分可能性の定義と性質
2 微分可能性の例

微分可能性の定義と性質

最初に

微分可能性の定義
微分可能性と連続性の関係

をみておきましょう．

微分可能性の定義

関数が微分可能であるとは次のように定義されます．

[微分可能性]　関数$f(x)$と実数$a$に対して，極限

$\begin{align*} \lim_{b\to a}\frac{f(b)-f(a)}{b-a}\bra{=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}} \end{align*}$

が有限の値として存在するとき，$f(x)$は$x=a$で微分可能であるという．また，微分可能でないとき，微分不可能であるという．

定義式は

$\lim\limits_{b\to a}\dfrac{f(b)-f(a)}{b-a}$
$\lim\limits_{h\to 0}\dfrac{f(a+h)-f(a)}{h}$

の２つ考えられますが，これらが等しいことについては以下の記事で説明しています．

【ワンポイント数学５｜２つの微分の定義式を図から理解しよう】

$x=a$での関数$f(x)$の微分係数を求める際には，$f(x)$の$x=a$から少し動かした場合の平均変化率を考えることになります．その際，「$a$から$a+h$までの平均変化率」と考えるか「$a$から$b$までの平均変化率」と考えるかで定義式は２種類考えられます．

微分可能性を考えるときには

どの関数が
どこで

という２つが重要です．

直感的には，「$f(x)$が$x=a$で微分可能である」とは，「グラフ$y=f(x)$は$x=a$で『接線が引ける』=『なめらか』である」ということを表しています．

また，前後しますが，極限についても定義を確認しておきましょう．

[極限]　関数$f(x)$と実数$a$に対して，極限$\lim\limits_{x\to a}f(x)$が存在するとは，

$x>a$で$x\to a$とする右極限$\lim\limits_{x\to a+0}f(x)$
$x<a$で$x\to a$とする左極限$\lim\limits_{x\to a-0}f(x)$

が共に存在して一致することをいう．なお，$a=0$のときは

右極限を$\lim\limits_{x\to +0}f(x)$
左極限を$\lim\limits_{x\to -0}f(x)$

と書く．

この「右極限」と「左極限」は数学IIIの範囲ですね．

関数$f(x)$が$x=a$で微分可能であるとは，図形的には$y=f(x)$のグラフが$x=a$で滑らかであるということである．

連続性の定義

次に連続性の定義を確認しましょう．

[連続性]　関数$f(x)$と実数$a$に対して，$\lim\limits_{x\to a}f(x)$が存在して$f(a)$に一致するとき，$f(x)$は$x=a$で連続であるという．また，連続でないとき不連続であるという．

微分可能性と同様に，連続性を考えるときには

どの関数が
どこで

という２つが重要です．

直感的には，「$f(x)$が$x=a$が連続である」とは，「グラフ$y=f(x)$が$x=a$で『繋がっている』」ということを表しています．

逆に「$f(x)$が$x=a$が不連続である」とは，「グラフ$y=f(x)$が$x=a$で『切れて』いる」ということになります．

また，「$\lim\limits_{x\to a}f(x)$が存在して」いても，それが「$f(a)$に一致」していなければ連続ではありません．

関数$f(x)$が$x=a$で連続であるとは，図形的には$y=f(x)$のグラフが$x=a$で繋がっているということである．

微分可能性と連続性の関係

次の[微分可能性と連続性]は重要です．

[微分可能性と連続性]　関数$f(x)$と実数$a$に対して，$f(x)$が$x=a$で微分可能であれば$f(x)$は$x=a$で連続である．

パッと書かれるとピンとこないかも知れませんが，

　関数$f(x)$が$x=a$で微分可能
→$y=f(x)$のグラフは$x=a$でなめらかである
→前提としてグラフは繋がっていなければならない
→連続でなければならない

と考えれば，直感的に理解できますね．

関数$f(x)$と実数$a$に対して，$f(x)$が$x=a$で微分可能であることから，極限

$\begin{align*} \lim\limits_{b\to a}\frac{f(b)-f(a)}{b-a} \end{align*}$

が有限の値として存在する．この極限値を$\alpha$とすると，

$\begin{align*} &\lim_{b\to a}(f(b)-f(a)) \\=&\lim_{b\to a}\frac{f(b)-f(a)}{b-a}\cdot(b-a) \\=&\alpha\cdot0 =0 \end{align*}$

が成り立つ．以上より，$f(x)$が$x=a$で連続であることが従う．

極限

$\begin{align*} \lim_{b\to a}\frac{f(b)-f(a)}{b-a} \end{align*}$

について，分母は$\lim\limits_{b\to a}(b-a)=0$なので，もし分子の極限が０でなければ$\lim\limits_{b\to a}\dfrac{f(b)-f(a)}{b-a}$が有限の値になり得ませんから，分子の極限も０になるしかないというところですね．

さて，[微分可能性と連続性]の対偶も大切です．

関数$f(x)$と実数$a$に対して，$f(x)$が$x=a$で不連続であれば，$f(x)$は$x=a$で微分不可能である．

なお，[微分可能性と連続性]の逆は成り立たないことに注意してください．つまり，連続であっても微分不可能であることもありえます．

微分可能性は連続性の上に成り立つから，そもそも不連続なら微分不可能である．

微分可能性の例

それでは，いくつか例を考えます．

次のそれぞれの関数$f(x)$は$x=0$で微分可能か．

$f(x)=\begin{cases}x&(x<0)\\ x+1&(x\geqq0)\end{cases}$
$f(x)=\begin{cases}x&(x\neq0)\\ 1&(x=0)\end{cases}$
$f(x)=|x|$
$f(x)=\begin{cases}0&(x<0)\\ x^2&(x\geqq0)\end{cases}$

例１

関数

$\begin{align*} f(x)=\begin{cases}x&(x<0)\\ x-1&(x\geqq0)\end{cases} \end{align*}$

について，右極限は

$\begin{align*} \lim_{x\to+0}f(x)=\lim_{x\to+0}(x-1)=-1 \end{align*}$

であり，左極限は

$\begin{align*} \lim_{x\to-0}f(x)=\lim_{x\to-0}x=0 \end{align*}$

だから，右極限と左極限は一致しない．

よって，極限$\lim\limits_{x\to0}f(x)$が存在しないから$f(x)$は$x=0$で不連続なので，$f(x)$は$x=0$で微分不可能である．

例２

関数

$\begin{align*} f(x)=\begin{cases}x&(x\neq0)\\ 1&(x=0)\end{cases} \end{align*}$

について，右極限は

$\begin{align*} \lim_{x\to+0}f(x)=\lim_{x\to+0}x=0 \end{align*}$

であり，左極限は

$\begin{align*} \lim_{x\to-0}f(x)=\lim_{x\to-0}x=0 \end{align*}$

だから，右極限と左極限は一致するので，極限$\lim\limits_{x\to0}f(x)$が存在して０となる．

しかし，$f(0)=1$だから，$\lim\limits_{x\to0}f(x)\neq f(0)$となって$f(x)$は$x=0$で不連続である．したがって，$f(x)$は$x=0$で微分不可能である．

右極限$\lim\limits_{x\to+0}f(x)$と$f(0)$が異なっていれば不連続となるので，

「$\lim\limits_{x\to+0}f(x)==0\neq1=f(0)$だから$f(x)$は$x=0$で不連続」

としても問題ありません．

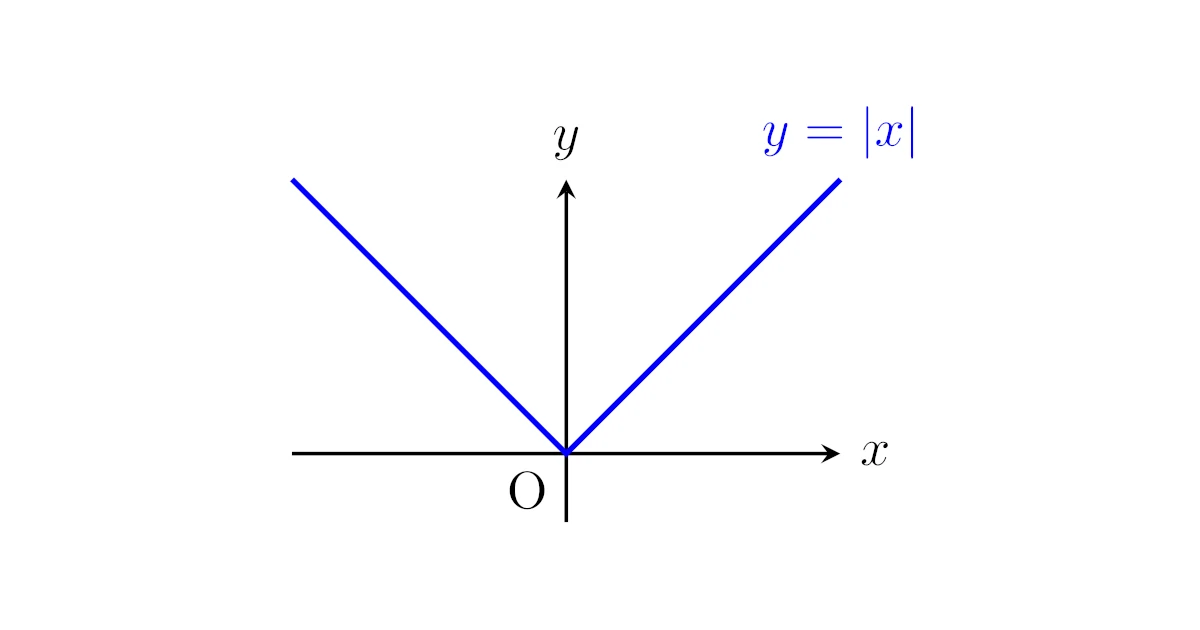
例３

関数f(x)=|x|について，$\dfrac{f(b)-f(0)}{b-0}$の右極限は

$\begin{align*} \lim_{b\to+0}\frac{f(b)-f(0)}{b-0} =&\lim_{b\to+0}\frac{|b|-|0|}{b} \\=&\lim_{b\to+0}\frac{b}{b} \\=&\lim_{b\to+0}1 =1 \end{align*}$

であり，左極限は

$\begin{align*} \lim_{b\to-0}\frac{f(b)-f(0)}{b-0} =&\lim_{b\to-0}\frac{|b|-|0|}{b} \\=&\lim_{b\to-0}\frac{-b}{b} \\=&\lim_{b\to-0}(-1) =-1 \end{align*}$

だから，右極限と左極限は一致せず$f(x)$は$x=0$で微分不可能である．

まず$y=f(x)$のグラフは$x=0$で「尖っている」ので微分不可能なように見えますが，$f(x)$は$x=0$で連続なので例１，例２のように「不連続性から微分不可能」とはできません．

よって，微分可能であることは定義から示す必要があるわけですね．

なお，証明において

$b>0$なら$|b|=b$
$b<0$なら$|b|=-b$

であることに注意してください．

【参考記事：ワンポイント数学２｜絶対値の定義から一瞬で解ける問題】

$a$の絶対値$|a|$は，$a\geqq0$のとき$|a|=a$, $a<0$のとき$|a|=-a$となります．ただ，これは定義ではなく，定義から導かれる性質です．定義のイメージがしっかりあれば，不等式$|x-3|\leqq5$や方程式$|x-2|+|x-4|=5$はほぼ計算することなく解を求めることができます．

例４

関数

$\begin{align*} f(x)=\begin{cases}0&(x<0)\\ x^2&(x\geqq0)\end{cases} \end{align*}$

について，$\dfrac{f(b)-f(0)}{b-0}$の右極限は

$\begin{align*} \lim_{b\to+0}\frac{f(b)-f(0)}{b-0} =&\lim_{b\to+0}\frac{b^2-0^2}{b} \\=&\lim_{b\to+0}\frac{b^2}{b} \\=&\lim_{b\to+0}b =0 \end{align*}$

であり，左極限は

$\begin{align*} \lim_{b\to-0}\frac{f(b)-f(0)}{b-0} =&\lim_{b\to-0}\frac{0-0}{b} \\=&\lim_{b\to-0}\frac{0}{b} \\=&\lim_{b\to-0}0 =0 \end{align*}$

だから，右極限と左極限は一致し，$f(x)$は$x=0$で微分可能である．

このように，$x=0$を境目にして異なる式で表されていても，「つなぎ目」の境界でなめらかに繋がっていれば，微分可能となります．

チョココロネより:

2020年12月20日 10:32 PM

関数の極限値を出す際、関数が連続していれば、その関数値を極限値とし、連続していない場合は右極限、左極限を考えますが、そもそも関数が連続しているのは右極限、左極限が一致する場合ですよね？
連続しているなら代入したのを極限値としてもよい↔極限値が一致すれば連続
堂々巡りになりませんか？
よろしくお願いします。

返信
- 山本拓人より:
  
  2020年12月25日 12:51 AM
  
  ご質問をありがとうございます！この記事のどの部分への質問なのか分からないのですが，ご質問にお答えします．
  
  まず連続性の定義について整理します．次の２つに分けると分かりやすいでしょう．
  - 右極限$\lim\limits_{x\to a+0}f(x)$と左極限$\lim\limits_{x\to a-0}f(x)$が一致するとき，これらの値を$\lim\limits_{x\to a}f(x)$で表し，$f(x)$の$x=a$での極限という．
  - 極限$\lim\limits_{x\to a}f(x)$と$f(a)$が一致するとき，$f(x)$は$x=a$で連続という．
  これらを１つにまとめると「$x=a$での右極限と左極限と$f(a)$が一致するとき，$f(x)$は$x=a$で連続という」となります．
  
  これを踏まえると，以下のようにお答えできます．
  - 極限と値が一致するのが連続の定義ですから，「連続しているなら代入したのを極限値としてもよい」のは当たり前ですね．
  - 「極限値が一致すれば連続」というのは，「極限値$\lim\limits_{x\to a}f(x)$が($f(a)$に)一致すれば連続」の意味で書かれているなら，まさに連続性の定義そのものですね．
  ということで，いずれも連続性の定義から明らかな主張を述べていらっしゃるだけで，堂々巡りにはなっていません．
  
  返信

ワンステップ数学５｜微分不可能な例と直感的な理解

微分可能性の定義と性質

微分可能性の定義

連続性の定義

微分可能性と連続性の関係

微分可能性の例

例１

例２

例３

例４

コメント