と無限に足していくときの和を$\sum\limits_{k=1}^{\infty}a_k$と表し,数列$\{a_n\}$の無限級数というのでした.
正確には極限$\lim\limits_{n\to\infty}(a_1+a_2+\dots+a_n)$のことですね.
一般に無限級数$\sum\limits_{k=1}^{\infty}a_k$の収束・発散の判定は簡単でない場合も多いのですが,数列$\{a_k\}$が等比数列の場合には簡単に収束・発散が判定できます.
このように,等比数列の無限級数は性質が分かりやすく重要なので,無限等比級数と名前が付いています.
この記事では,
- 無限等比級数とは何か?
- 無限等比級数の収束・発散の判定方法
- 無限等比級数の具体例
を順に説明します.
「極限」の一連の記事
無限等比級数とは
無限等比級数を定義して,どのように大切なのかを解説します.
無限等比級数の例
無限等比級数は以下のように定義されます.
たとえば
- $1+2+4+8+\dots+2^{n-1}+\dots$
- $\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dots+\dfrac{1}{2^n}+\dots$
- $2-\dfrac{2}{3}+\dfrac{2}{9}-\dfrac{2}{27}+\dots+2\bra{-\dfrac{1}{3}}^{n-1}+\dots$
はいずれも無限等比級数で,それぞれ
と表すこともできますね.
なぜ無限等比級数が重要なのか
そもそも数列とは数の並べたものことなので,分かりやすい規則があろうがなかろうが数が並んでさえいればそれは数列です.
そう考えると,素性のよく分からない数列$\{a_n\}$の無限級数$\sum\limits_{n=1}^{\infty}a_n$を考えるのは難しいでしょうし,逆によく分かっている数列$\{a_n\}$の無限級数$\sum\limits_{n=1}^{\infty}a_n$は考えやすいものになりそうですね.
そのため,無限級数$\sum\limits_{n=1}^{\infty}a_n$の収束・発散の判定は難しいことも多く,
といった単純そうに見える無限級数でさえ,収束・発散の判定は面倒です.
$\sum\limits_{n=1}^{\infty} \dfrac{1}{n^2}$は収束しますが,$\sum\limits_{n=1}^{\infty} \dfrac{1}{n}$は$\infty$に発散します.とくに前者の$\sum\limits_{n=1}^{\infty} \dfrac{1}{n^2}$の極限値を求める問題はバーゼル問題と呼ばれており,レオンハルト・オイラーが$\dfrac{\pi^2}{6}$となることを証明するまでは未解決問題でした.
無限級数の中でも,無限等比級数は非常に分かりやすいもので,
- 収束するための必要十分条件
- 収束する場合にはその極限値
がよく分かっています.これが無限等比級数が重要な理由です.
無限等比級数の収束・発散条件
無限等比級数は次のように収束・発散します.
[無限等比級数の収束・発散]初項$a$,公比$r$の等比数列$\{a_n\}$に対して,無限等比級数$\sum\limits_{k=1}^{\infty}a_n$が収束するための必要十分条件は
- $a=0$
- $-1<r<1$
のいずれかを満たすことである.また,無限等比級数$\sum\limits_{k=1}^{\infty}a_n$が収束するとき
となる.
無限級数$\sum\limits_{n=1}^{\infty}a_n$が収束するには,少なくとも数列$\{a_n\}$が0に収束していなければならなかったことを思い出しておきましょう.
もし等比数列$\{a_n\}$の初項が0でなければ,公比が$r<-1$または$1<r$であれば等比数列$\{a_n\}$は発散するので,無限等比級数$\sum\limits_{n=1}^{\infty}a_n$は問答無用で発散することが分かります.
また,$r=1$であれば等比数列$\{a_n\}$は$a$に収束しますが,$a\neq0$ならこの場合もやはり無限等比級数$\sum\limits_{n=1}^{\infty}a_n$は発散しますね.
一方,$a=0$または$-1<r<1$であれば,等比数列の和の公式から直接極限を求めることができます.
この考え方さえ分かっていれば瞬時に導出できるので,覚えるのではなく理解して使えるようにしてください.
きちんと証明の形にすると次のようになります.
数列$\{a_n\}$の一般項は$a_n=ar^{n-1}$と表せる.
[1]$a=0$のときは,任意の正の整数$n$に対して$a_n=0$だから
と収束する.
[2]$-1<r<1$のときは,$\lim\limits_{n\to\infty}r^n=0$と等比数列の和の公式を併せて
と収束する.
[3]$a\neq0$かつ「$r<-1$または$1<r$」のときは,等比数列$\{a_n\}$が発散するから$\sum\limits_{n=1}^{\infty}a_n$も発散する.
[4]$a\neq0$かつ$r=1$のときは,数列$\{a_n\}$は$a$に収束する.$a\neq0$だから$\sum\limits_{n=1}^{\infty}a_n$も発散する.
[1]〜[4]より,収束するための必要十分条件は$a=0$または$-1<r<1$であり,このとき
と収束する.
無限等比級数の具体例
例1(発散する無限等比級数)
無限級数$\sum\limits_{n=1}^{\infty}2^{n-1}$の極限の収束・発散を調べよ.収束する場合はその極限値も求めよ.
実際に書き並べて和を表すと
ですから,どんどん項が大きくなって発散することが見てとれますね.
そもそも$\{2^{n-1}\}$が0に収束していないので,その時点で発散と言っても良いですね.
例2(収束する無限等比級数)
無限級数$\sum\limits_{n=1}^{\infty}\dfrac{1}{2^n}$の極限の収束・発散を調べよ.収束する場合はその極限値も求めよ.
実際に書き並べて和を表すと
ですから,公比が$\dfrac{1}{2}$の無限等比級数なので収束しますね.
無限級数$\sum\limits_{n=1}^{\infty}\dfrac{1}{2^n}$は初項$\dfrac{1}{2}$,公比$\dfrac{1}{2}$の等比数列の無限等比級数である.
公比$\dfrac{1}{2}$が$-1<\dfrac{1}{2}<1$を満たすから収束し,
である.
例3(収束する無限等比級数)
無限級数$\sum\limits_{n=1}^{\infty}2\Bigl(-\dfrac{1}{3}\bigr)^{n-1}$の極限の収束・発散を調べよ.収束する場合はその極限値も求めよ.
実際に書き並べて和を表すと
ですから,公比が$-\dfrac{1}{3}$の無限等比級数なので収束しますね.
無限級数$\sum\limits_{n=1}^{\infty}2\Bigl(-\dfrac{1}{3}\bigr)^{n-1}$は初項2,公比$-\dfrac{1}{3}$の等比数列の無限等比級数である.
公比$-\dfrac{1}{3}$が$-1<-\dfrac{1}{3}<1$を満たすから収束し,
である.
1と${0.999\dots}$が等しい話
小学校では$0.3333\dots$や$0.7878\dots$のような無限小数を学びます.
しかし,実は無限小数をきちんと理解するには無限級数の知識を必要とします.
無限級数は一見不思議な性質を持っており,たとえば
が成り立ちます.
最初は本当にこの等式が成り立つのか怪しく感じてしまうかもしれませんが,無限小数の定義をきちんと追えば証明することができます.
以下の記事では,$1=0.999\dots$がどうして成り立つのかを直感的に説明したのち,厳密な無限小数の定義も説明しています.
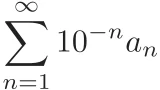
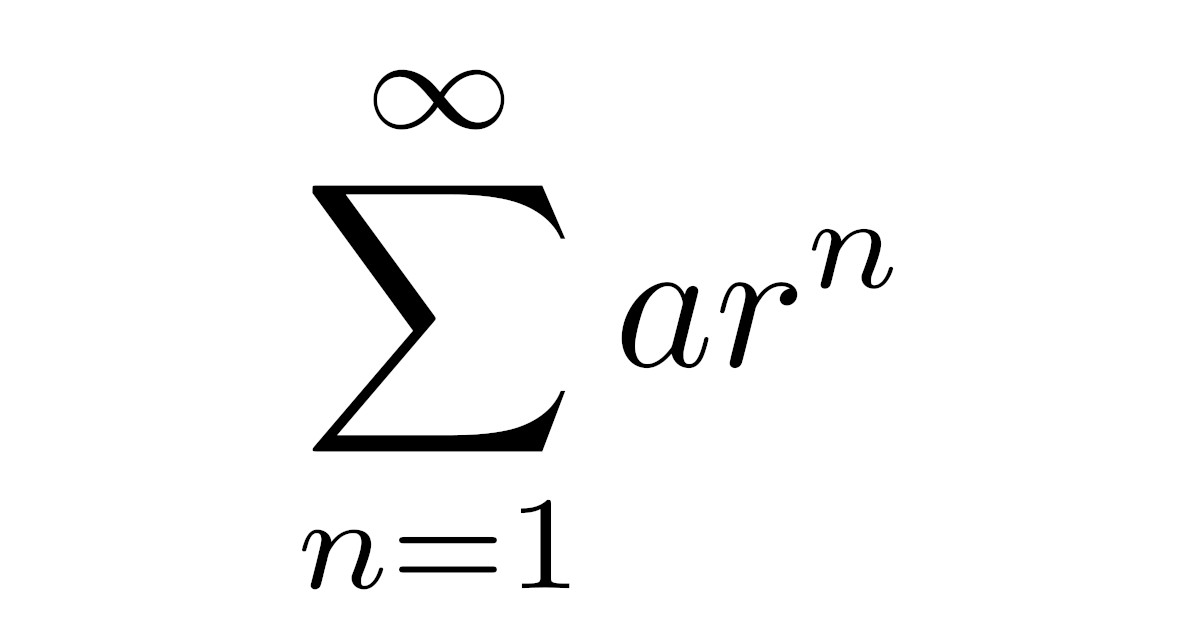
コメント