$\ang{B}=90^\circ$の直角三角形$\tri{ABC}$について,$\theta=\ang{A}$としたときの3種類の辺の比を
と名付けたものを三角比というのでした.
三角形の内角の和は常に$180^\circ$だったので,$\theta=\ang{A}$は$0^{\circ}<\theta<90^{\circ}$の範囲しか動きません.
そこで,単位円を使うことで$0^\circ\leqq\theta\leqq180^\circ$の場合にも$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$が定義できることを以前の記事で説明しました.
同じ方法を用いると,さらに広く全ての実数$\theta$に対して$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$を定義することができ,このときこれらを三角関数と呼びます.
この記事では,
- 偏角(三角関数の準備)
- 三角関数の定義
を順に解説します.
「三角関数」の一連の記事
偏角(三角関数の準備)
三角関数を定義するために偏角を準備しておきましょう.ざっくり言えば,向きのついた角を偏角といいます.
$xy$平面上の原点$\mrm{O}$とは異なる点$\mrm{P}$に対して,$x$軸の正方向からベクトル$\Ve{OP}$への有向角を($x$軸正方向からの)点$\mrm{P}$の偏角という.ただし,反時計回りを正とする.
具体例1(負の偏角)
$xy$平面上の$x$軸正方向からの偏角が$-40^{\circ}$の点$\mrm{Q}$を1点図示せよ.
下図の点$\mrm{Q}$は$xy$平面上の$x$軸正方向からの偏角が$-40^{\circ}$の点である.
具体例2(360°を超える偏角)
$xy$平面上の$x$軸正方向からの偏角が$390^{\circ}$の点$\mrm{R}$を1点図示せよ.
下図の点$\mrm{R}$は$xy$平面上の$x$軸正方向からの偏角が$390^{\circ}$の点である.
三角関数の定義
偏角を定義してしまえば,三角比を$0^\circ\leqq\theta\leqq180^\circ$にまで拡張したのと同じ考え方で,任意の実数$\theta$に対して$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$を定義することができます.
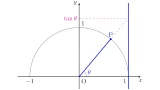
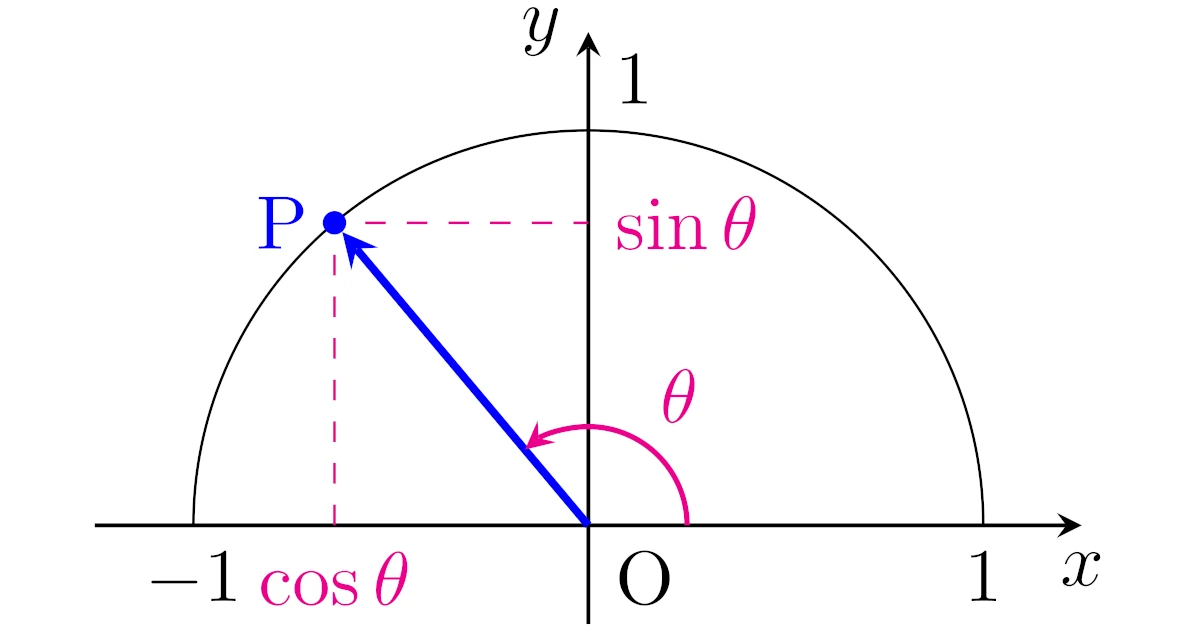
三角関数の定義
三角関数の定義は以下の通りです.
$\theta$を実数とする.このとき,偏角$\theta$の単位円周上の点$\mrm{P}$について,
- $\mrm{P}$の$x$座標を$\cos{\theta}$
- $\mrm{P}$の$y$座標を$\sin{\theta}$
と定義する.
また,$\cos{\theta}\neq0$のとき,$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$と定義する.
このように,単位円を使って任意の実数$\theta$に対して定義された$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$を三角関数と呼びます.
定義の点$\mrm{P}$の$x$座標が$\cos{\theta}=0$だったので,このとき($\theta=\pm90^\circ,\pm270^\circ,\dots$のとき)$\tan{\theta}$は定義できないことになります.
数学において0で割ってはいけないため,$\cos{\theta}\neq0$のときのみ$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$を定義するわけですね.
$\tan$の図形的意味
$xy$平面上の直線$x=1$と直線$\mrm{OP}$の交点の$y$座標が$\tan\theta$となります.
これも三角比を$0^\circ\leqq\theta\leqq180^\circ$に拡張したときと同じですね.
4つの関係式
$\sin$, $\cos$, $\tan$に関する4つの関係式も三角比の場合と同様に成り立ちます.
実数$\theta$について,
- $\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$
- $\cos^{2}{\theta}+\sin^{2}{\theta}=1$
- $1+\tan^{2}{\theta}=\dfrac{1}{\cos^{2}{\theta}}$
- $1+\dfrac{1}{\tan^{2}{\theta}}=\dfrac{1}{\sin^{2}{\theta}}$
が成り立つ.ただし,3つ目の公式は$\cos{\theta}\neq0$,4つ目の公式は$\sin{\theta}\neq0$,$\cos{\theta}\neq0$とする.
最後の条件は$\tan{\theta}$が定義されており,分母が0になってはいけないためにあります.
これらの4つの関係式はそれぞれ
- $\tan$と$\cos$と$\sin$の関係式
- $\cos$と$\sin$の関係式
- $\cos$と$\tan$の関係式
- $\sin$と$\tan$の関係式
となっていることは意識しておきたいところです.これが意識できていれば
- $\cos$から$\sin$を求めるときは公式$\cos^{2}{\theta}+\sin^{2}{\theta}=1$
- $\tan$から$\sin$を求めるときは公式$1+\dfrac{1}{\tan^{2}{\theta}}=\dfrac{1}{\sin^{2}{\theta}}$
といったように,どの公式を使うのがよいかは自然に見えてくるはずですね.
コメント