まずは三角比に関する次の問題を考えましょう.
$\sin{25^{\circ}}-\cos{65^{\circ}}$の値を求めよ.
この問題は$\sin{25^{\circ}}$, $\cos{65^{\circ}}$の角度が$25^{\circ}$と$65^{\circ}$で異なっているので,これらを揃えたいところです.
実際,三角比の$(90^\circ-\theta)$型の公式を用いることで,角度を揃えることができて値を求めることができます.
この記事では
- 三角比の$(90^\circ-\theta)$型の変換公式
- 三角比の$(90^\circ-\theta)$型の変換公式の具体例
- 三角比の$(90^\circ-\theta)$型の変換公式の証明
を順に説明します.
「三角比」の一連の記事
三角比の$(90^\circ-\theta)$型の変換公式
まずは有名角の三角比の観察から$(90^\circ-\theta)$型の公式を予想してから($90^\circ-\theta$)型の公式を紹介します.
有名角の三角比の観察からの予想($\sin$と$\cos$)
有名角($\theta=30^\circ,45^\circ,60^\circ$)の三角比$\sin{\theta}$, $\cos{\theta}$は以下のようになっているのでした.
| $\theta$ | $30^\circ$ | $45^\circ$ | $60^\circ$ |
|---|---|---|---|
| $\sin{\theta}$ | $\sin{30^\circ}=\dfrac{1}{2}$ | $\sin{45^\circ}=\dfrac{\sqrt{2}}{2}$ | $\sin{60^\circ}=\dfrac{\sqrt{3}}{2}$ |
| $\cos{\theta}$ | $\cos{30^\circ}=\dfrac{\sqrt{3}}{2}$ | $\cos{45^\circ}=\dfrac{\sqrt{2}}{2}$ | $\cos{60^\circ}=\dfrac{1}{2}$ |
この表で等しいものを探すと,
- $\sin{30^\circ}=\cos{60^\circ}\Bigl(=\frac{\sqrt{3}}{2}\Bigr)$
- $\sin{45^\circ}=\cos{45^\circ}\Bigl(=\frac{\sqrt{2}}{2}\Bigr)$
- $\sin{60^\circ}=\cos{30^\circ}\Bigl(=\frac{1}{2}\Bigr)$
が見つかりますね.このことから「$\theta+\varphi=90^\circ$なら$\sin{\theta}$と$\cos{\varphi}$は等しいのではないか?」という予想が立ちます.つまり,
が成り立つのではないかと予想できます.
有名角の三角比の観察からの予想($\tan$)
また,有名角($\theta=30^\circ,45^\circ,60^\circ$)の三角比$\tan{\theta}$は以下のようになっているのでした.
| $\theta$ | $30^\circ$ | $45^\circ$ | $60^\circ$ |
|---|---|---|---|
| $\tan{\theta}$ | $\tan{30^\circ}=\dfrac{1}{\sqrt{3}}$ | $\tan{45^\circ}=1$ | $\tan{60^\circ}=\sqrt{3}$ |
この表から
- $\tan{30^\circ}=\dfrac{1}{\tan{60^\circ}}\bigl(=\sqrt{3}\bigr)$
- $\tan{45^\circ}=\dfrac{1}{\tan{45^\circ}}\bigl(=1\bigr)$
が成り立っているので,このことから「$\theta+\varphi=90^\circ$なら$\tan{\theta}$と$\dfrac{1}{\tan{\varphi}}$は等しいのではないか?」という予想が立ちます.つまり,
が成り立つのではないかと予想できます.
$(90^\circ-\theta)$型の変換公式
実際,いまの予想は正しく次の$(90^{\circ}-\theta)$型の三角比の変換公式が成り立ちます.
$0<\theta<90^\circ$なる実数$\theta$について,
の3つの関係式が成り立つ.
上の有名角の三角比での観察ができれば,この公式は覚えなくても自然と予想できますね.
また,この変換公式の証明が分かれば,より直感的に「見て」納得できます.
この$(90^{\circ}-\theta)$型の三角比の変換公式はこの記事の最後で証明しています.
$(90^\circ-\theta)$型の変換公式の具体例
証明はこの記事の最後に回し,先に具体例を考えておきましょう.
例1($\sin$と$\cos$)
$\sin{35^\circ}-\cos{55^\circ}$の値を求めよ.
この問題のように三角比の角度が統一されていない場合には,角度を揃えて計算できるようにしたいところです.
いまは$35^\circ+55^\circ=90^\circ$なので,$(90^{\circ}-\theta)$型の変換公式を使えば角度が揃えられますね.
$(90^{\circ}-\theta)$型の変換公式より
なので,$\sin{35^\circ}-\cos{55^\circ}=0$となる.
三角比の定義に立ち帰ると,下図のような$35^\circ$, $55^\circ$の内角をもつ直角三角形を考えることになります.
この図より$\sin{25^\circ}$と$\cos{65^\circ}$は等しいことが分かりますから,確かに$\sin{25^\circ}-\cos{65^\circ}=0$となりますね.
例2($\sin$と$\cos$)
$\sin^2{25^{\circ}}+\sin^2{65^{\circ}}$の値を求めよ.
この問題も$25^\circ+65^\circ=90^\circ$なので,$(90^{\circ}-\theta)$型の変換公式を使えば角度が揃えられますね.
例3($\sin$と$\cos$と$\tan$)
$\tan^{2}{14^{\circ}}-\dfrac{1}{\sin{76^{\circ}}\cos{14^{\circ}}}$の値を求めよ.
やはりこの問題でも$14^\circ+76^\circ=90^\circ$なので,$(90^{\circ}-\theta)$型の変換公式を使えば角度が揃えられますね.
$(90^{\circ}-\theta)$型の変換公式より
なので,$\tan$と$\cos$の関係式$1+\tan^{2}{\theta}=\dfrac{1}{\cos^{2}{\theta}}$と併せて
となる.
$(90^\circ-\theta)$型の変換公式の証明
直角三角形を裏返した図が見えれば,三角比の$(90^{\circ}-\theta)$型の公式は証明できます.
(再掲)$0<\theta<90^\circ$なる実数$\theta$について,
の3つの関係式が成り立つ.
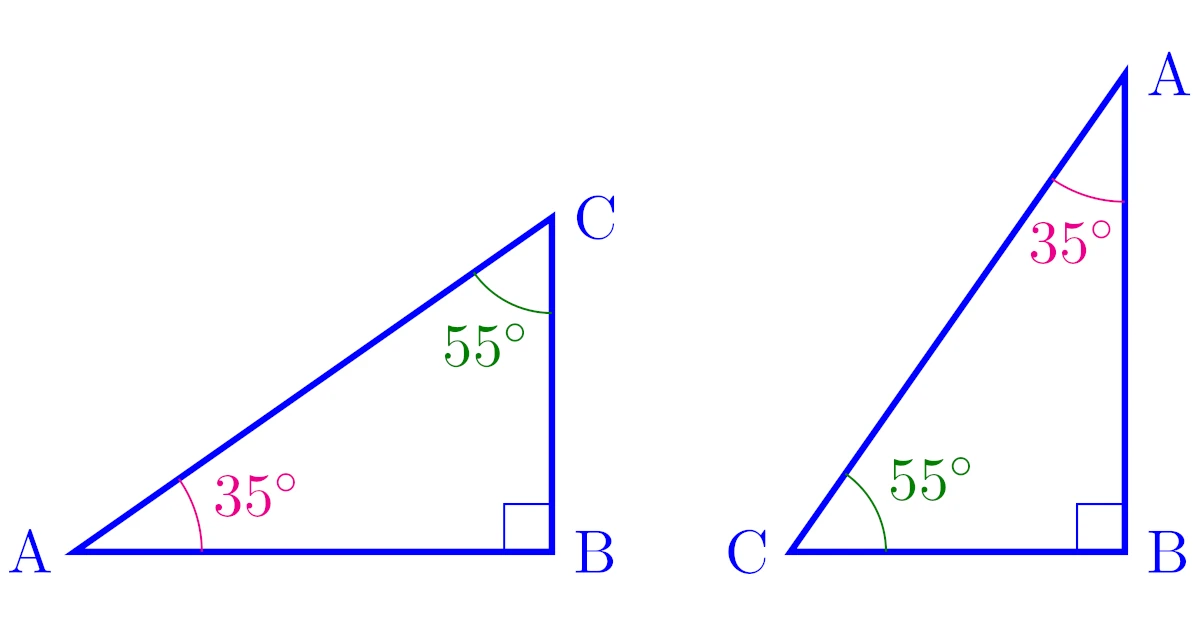
$\ang{A}=\theta$, $\ang{B}=90^{\circ}$の直角三角形$\tri{ABC}$を考える.
このとき,$\ang{C}=180^\circ-90^\circ-\theta=90^\circ-\theta$なので,下図のように描ける.
左の図で三角比の定義を考えると
であり,右の図で三角比の定義を考えると
である.よって,$(*)$と$(**)$から
が成り立つ.
このように裏返した直感三角形が見えれば,$(90^{\circ}-\theta)$型の公式は難しくないですね.
コメント