ベクトルの内積の定義と展開公式｜内積はなぜ大切なのか？

実数倍・和・差に加えて，ベクトルの重要な計算には内積と呼ばれるものがあります．

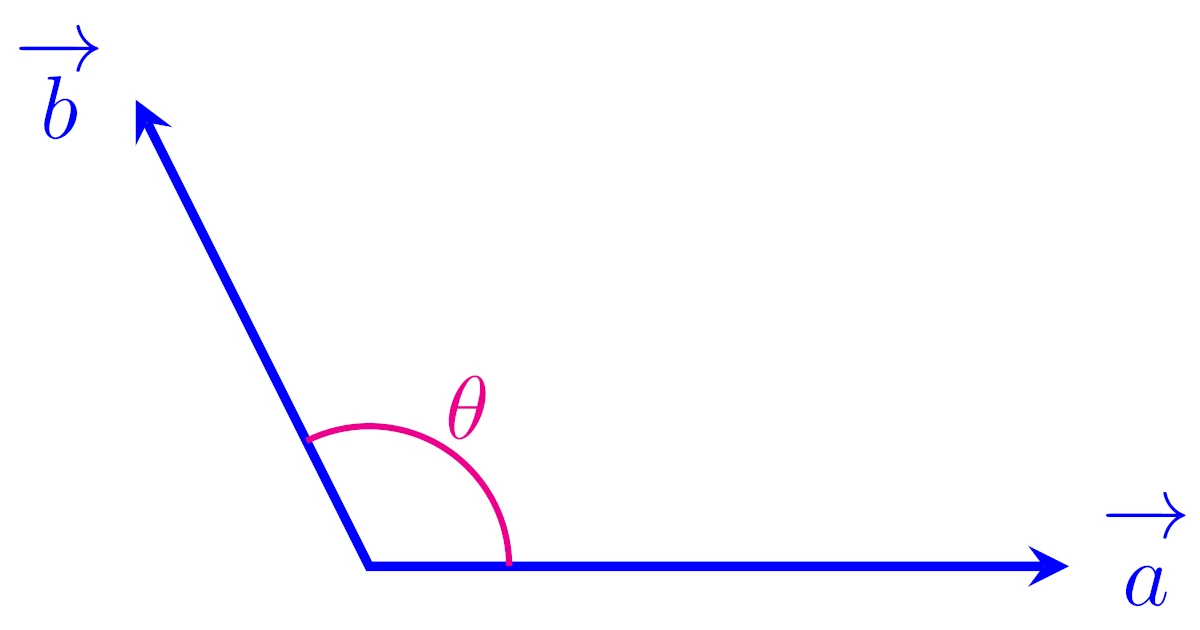
ベクトル$\ve{a}$, $\ve{b}$の内積は，ベクトルの長さ$|\ve{a}|$, $|\ve{b}|$と，$\ve{a}$と$\ve{b}$の間の角の大きさ$\theta$をもとに定義されます．

２つのベクトル$\ve{a}$, $\ve{b}$の内積を考えることによって，和や差の大きさ$|\ve{a}\pm\ve{b}|$を計算できたり，図形の面積や角度なども求められるようになります．

この記事では

ベクトルの和・差の大きさ
内積の定義とベクトルの和・差の展開公式
内積の具体例

を順に説明します．

「ベクトル」の一連の記事

ベクトルの和・差の大きさ
1. 平行なベクトルの和の長さ
2. 余弦定理の復習
内積の定義とベクトルの和・差の展開公式
1. 内積の定義
2. ベクトルの展開公式
内積の具体例
1. ベクトルの差の大きさの求め方
2. 補足

ベクトルの和・差の大きさ

ベクトルの内積がどのように大切かをみるために，まずはベクトルの和・差$\ve{a}+\ve{b}$, $\ve{a}-\ve{b}$の長さ

$\begin{align*}|\ve{a}+\ve{b}|,\quad |\ve{a}-\ve{b}|\end{align*}$

がどのように求められるか考えましょう．

平行なベクトルの和の長さ

２つのベクトル$\ve{a}$, $\ve{b}$が同じ向きであれば，これらの和$\ve{a}+\ve{b}$の長さは

$\begin{align*}|\ve{a}+\ve{b}|=|\ve{a}|+|\ve{b}|\end{align*}$

となりますね．

同様に，$\ve{a}$と$\ve{b}$が逆向きの場合には長さの差で求まります．

しかし，$\ve{a}$と$\ve{b}$が平行でない場合には，$|\ve{a}+\ve{b}|$や$|\ve{a}-\ve{b}|$はそう単純には求められませんね．

余弦定理の復習

$\ve{a}$と$\ve{b}$が平行でない場合の$|\ve{a}+\ve{b}|$を求めるために，ここで余弦定理を復習しておきましょう．

余弦定理は２つの辺の長さとその間の角の大きさが絡む三角形において便利なのでした．

［余弦定理］$\tri{OAB}$について，次の等式が成り立つ．

$\begin{align*}\mrm{AB}^2=\mrm{OA}^2+\mrm{OB}^2-2\mrm{OA}\cdot\mrm{OB}\cdot\cos{\ang{O}}\end{align*}$

$\tri{OAB}$において，$\ve{a}=\Ve{OA}$, $\ve{b}=\Ve{OB}$, $\theta=\ang{O}$とすると，余弦定理の等式は

$\begin{align*}|\ve{a}-\ve{b}|^2=|\ve{a}|^2+|\ve{b}|^2-2|\ve{a}||\ve{b}|\cos{\theta}\quad\dots(*)\end{align*}$

となりますね．

この等式から，２つのベクトルの差$\ve{a}-\ve{b}$の大きさ$|\ve{a}-\ve{b}|$は

$\ve{a}$の大きさ$|\ve{a}|$
$\ve{b}$の大きさ$|\ve{a}|$
$\ve{a}$, $\ve{b}$の間の角の大きさ$\theta$

から求められることが分かりました．

内積の定義とベクトルの和・差の展開公式

それではいま考えたことから，ベクトルの内積を定義しましょう．

内積の定義

さて，余弦定理から得られる等式

$\begin{align*}|\ve{a}-\ve{b}|^2=|\ve{a}|^2+|\ve{b}|^2-2|\ve{a}||\ve{b}|\cos{\theta}\quad\dots(*)\end{align*}$

は$(a-b)^2$の展開公式

$\begin{align*}(a-b)^2=a^2+b^2-2ab\end{align*}$

によく似ています．

そこで$|\ve{a}||\ve{b}|\cos{\theta}$の部分を$\ve{a}$と$\ve{b}$の積であると考え，$\ve{a}$と$\ve{b}$の内積といいます．

$\ve{0}$でない２つのベクトル$\ve{a}$, $\ve{b}$に対して，$\ve{a}$の始点と$\ve{b}$の始点を一致させたときの２つのベクトルの間の角の大きさ$\theta(\leqq180^\circ)$を$\ve{a}$と$\ve{b}$のなす角という．

$\ve{0}$でない２つのベクトル$\ve{a}$, $\ve{b}$のなす角を$\theta$とするとき，

$\begin{align*}|\ve{a}||\ve{b}|\cos{\theta}\end{align*}$

を$\ve{a}$と$\ve{b}$の内積（inner product）といい$\ve{a}\cdot\ve{b}$と表す．

また，$\ve{a}=\ve{0}$または$\ve{b}=\ve{0}$のとき，内積$\ve{a}\cdot\ve{b}$を０と定める．

ベクトルの展開公式

内積$\ve{a}\cdot\ve{b}$を用いると，先ほどの余弦定理から得られる等式$(*)$は

$\begin{align*}|\ve{a}-\ve{b}|^2=|\ve{a}|^2+|\ve{b}|^2-2\ve{a}\cdot\ve{b}\end{align*}$

と表せますね．

つまり，内積$\ve{a}\cdot\ve{b}$を定義することで$|\ve{a}-\ve{b}|^2$は$(a-b)^2=a^2-2ab+b^2$と同様に展開できるようになったわけですね．

さらに，この$|\ve{a}-\ve{b}|^2$の展開公式で$-\ve{b}$を$\ve{b}$に置き換えれば

$\begin{align*}|\ve{a}+\ve{b}|^2=|\ve{a}|^2+2\ve{a}\cdot\ve{b}+|\ve{b}|^2\end{align*}$

となり，和の場合も$(a+b)^2=a^2+2ab+b^2$と同様に展開できることが分かります．

第２項では性質$-2\ve{b}\cdot(-\ve{a})=2\ve{a}\cdot\ve{b}$を用いています．この性質はのちの記事で説明します．

内積の具体例

内積を使うと，具体的には以下のような問題を解くことができます．

ベクトルの差の大きさの求め方

$|\ve{a}|=2$, $|\ve{b}|=3$のベクトル$\ve{a}$, $\ve{b}$のなす角が$60^\circ$のとき，$|\ve{a}-\ve{b}|$を求めよ．

$|\ve{a}-\ve{b}|^2$の展開公式

$\begin{align*}|\ve{a}-\ve{b}|^2=|\ve{a}|^2+|\ve{b}|^2-2\ve{a}\cdot\ve{b}\end{align*}$

を使えば求められそうです．いま$|\ve{a}|$と$|\ve{b}|$は分かっているので，あとは内積$\ve{a}\cdot\ve{b}$を求めれば，$|\ve{a}-\ve{b}|$が求まります．

内積$\ve{a}\cdot\ve{b}$は

$\begin{align*}\ve{a}\cdot\ve{b}=&|\ve{a}||\ve{b}|\cos{30^\circ}=2\cdot3\cdot\frac{1}{2}=3\end{align*}$

となるので，ベクトルの差の大きさの展開公式より

$\begin{align*}|\ve{a}-\ve{b}|^2&=|\ve{a}|^2-2\ve{a}\cdot\ve{b}+|\ve{b}|^2 \\&=2^2-2\cdot3+3^2=7\end{align*}$

となる．よって，$|\ve{a}-\ve{b}|=\sqrt{7}$である．

補足

先ほど見たように$|\ve{a}-\ve{b}|^2$の展開公式は余弦定理から得られるのでしたから，次の［別解］のように余弦定理を用いても本質的には全く同じです．

［別解］$\mrm{AC}\cdot\mrm{BC}\cos{60^\circ}$は

$\begin{align*}\mrm{AC}\cdot\mrm{BC}\cos{60^\circ}=2\cdot3\cdot\frac{1}{2}=3\end{align*}$

となるので，余弦定理より

$\begin{align*}\mrm{AB}^2=&\mrm{AC}^2-2\mrm{AC}\cdot\mrm{BC}\cos{60^\circ}+\mrm{BC}^2 \\=&2^2-2\cdot3+3^2=7\end{align*}$

となる．よって，$\mrm{AB}=\sqrt{7}$である．

いまの２つの解答を見比べると，確かに余弦定理

$\begin{align*}\mrm{AB}^2=\mrm{AC}^2-2\mrm{AC}\cdot\mrm{BC}\cos{\ang{C}}\end{align*}$

を使っているか，ベクトルの展開公式

$\begin{align*}|\ve{a}-\ve{b}|^2=|\ve{a}|^2-2\ve{a}\cdot\ve{b}+|\ve{b}|^2\end{align*}$

を使っているかの違いだけであることが分かりますね．