力のつりあいは物理の力学で,力の大きさを考える際の基本となる考え方です.力がつりあっている物体は
- 運動していれば等速直線運動をする
- 静止していれば静止し続ける
という性質が成り立ちます.
この記事では,力のつりあいの基本を解説し,具体例から力のつりあいを用いて力の大きさを求めます.
「力学の基本」の一連の記事
力のつりあい
まずは力のつりあいの基本を解説します.
力のつりあいとは?
簡単な具体例をみてみましょう.
具体例1
水平な床の上で物体が静止しているとき,物体にはたらく重力と床からの垂直抗力がつりあっています.
具体例2
水平な床の上で物体を左右から同じ力で糸で引っ張るとき,物体にはたらいている力はつりあっています.
力がつりあっているときの運動
力のつりあいについて,以下の事実が重要です.
[力のつりあい1]力がつりあっているとき,運動している物体は等速直線運動をする.
逆に,等速直線運動をしているとき,物体にはたらく力はつりあっている.
「静止し続けること」は「速さ0の等速直線運動をしていること」と言えるので,このことから次の事実も成り立ちます.
[力のつりあい2]力がつりあっているとき,静止している物体は静止し続ける.
逆に,物体が静止し続けているとき,物体にはたらく力はつりあっている.
たとえば,物体を荒い(摩擦力のはたらく)床の上に置いた物体を少し押しても動かないのは,押す力と摩擦力がつりあっているからですね.
また,カーリングのようにツルツルの氷の上に物体を滑らせてもほぼ等速直線運動をするのは,摩擦力がほとんどはたらかず物体にはたらく力がほぼつり合っているからですね.
具体例1(静止している2物体)
具体的に考えてみましょう.
問題
下図のように,滑車は台に固定されており,物体Aと物体Bはなめらかに動く滑車を通して糸でつながっている.また,物体は静止しているとする.
このとき,物体A, Bと滑車にはたらいている全ての力を書き込み,それぞれの力の大きさを求めよ.ただし,重力加速度を$g[\mrm{m/s^2}]$とする.
慣れればさほど難しくはありませんが,コツとしては
- 重力など必ずはたらく力を考える
- 物体と物体が接しているところに,垂直抗力,摩擦力がはたらくかを考える
です.
解答例
力を全て書き込むと下図のようになります.
これらの力の大きさは次のようになります(単位は全て$[\mrm{N}]$です).
- 物体A, Bにそれぞれ下向きに大きさ$Mg$, $mg$の重力がはたらく.
- 物体Aは静止しているから物体Aにはたらく「重力」「張力」はつりあっている.よって,物体Aに鉛直上向きに大きさ$mg$の張力がはたらく.
- 滑車を通しても糸の両端の張力の大きさは等しいから,滑車に鉛直した向きに,左向きに,物体Bに右向きに大きさ$mg$の張力がはたらく.
- 物体Bは静止しているから物体Bにはたらく水平方向の力「摩擦力」「張力」がつりあっている.よって,物体Bに左向きに大きさ$mg$の摩擦力がはたらく.
- 物体Bは静止しているから物体Bにはたらく鉛直方向の力「重力」「垂直抗力」がつりあっている.よって,物体Bに上向きに大きさ$Mg$の垂直抗力がはたらく.
何回も力のつりあいによって力の大きさを求めていることが分かりますね.
具体例2(静止している3物体)
いまの具体例1の台が物体Cになると,もう少し複雑になります.
問題
下図のように,物体Cには滑車が固定されており,物体Aと物体Bはなめらかに動く滑車を通して糸でつながっている.全ての物体は静止しているとする.
このとき,物体A, Bと滑車を併せた物体Cにはたらいている全ての力を書き込み,それぞれの大きさを求めよ.ただし,重力加速度を$g[\mrm{m/s^2}]$とする.
滑車は物体Cに固定されているので,滑車にはたらく力は物体Cにはたらく力と考えることに注意してください.
解答例
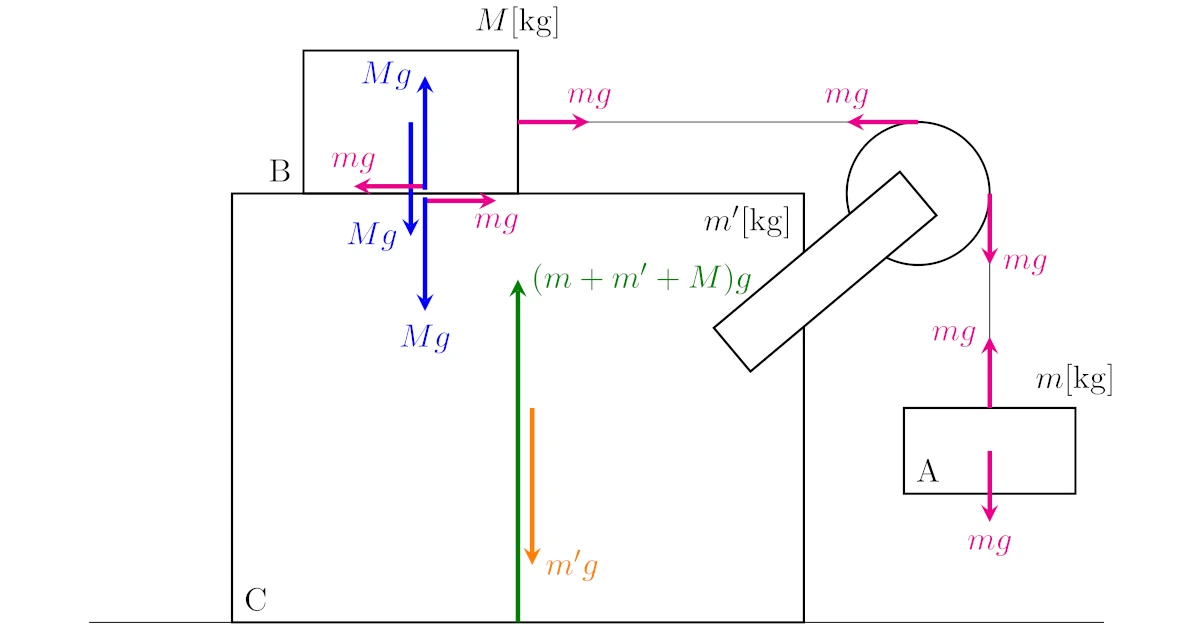
力を全て書き込むと下図のようになります.
こう見てみると意外と多くの力がはたらいていることが分かりますね.
床と物体Bは接触していますが,以下でみるように摩擦力ははたらきません.
この力の大きさは次のようになります(単位は全て$[\mrm{N}]$です).(5)までは途中までは上の具体例1と同じです.
- 垂直抗力と摩擦力は2物体にはたらく力の大きさは等しいから,物体Cに物体Bから鉛直上向きに大きさ$Mg$の垂直抗力,右向きに大きさ$mg$の摩擦力がはたらく.
- 物体Cは静止しているから物体C(と滑車)にはたらく鉛直方向の力「重力」「張力」「物体Bからの垂直抗力」「床からの垂直抗力」がつりあっている.よって,物体Cに床から鉛直上向きに大きさ$mg+m’g+Mg$の垂直抗力を受ける.
- 物体Cは静止しているから物体C(と滑車)にはたらく鉛直方向の力「張力」「Bからの摩擦力」「床からの摩擦力」がつりあっている.既に張力と物体Bからの摩擦力で既につりあっているので,床から摩擦力ははたらかない.
このように,静止している(等速直線運動をしている)物体にはたらく力の大きさを求める際には,力のつりあいがかなり重要だと分かりますね.
コメント