3次以上の多項式の因数分解を考えるとき,因数分解公式が使えない場合は因数定理を用いるのが定石です.
因数定理という名前を聞くと難しそうに感じてしまうかも知れませんが,実は因数定理はほとんど当たり前と言ってよいような定理です.
また,因数定理の兄弟姉妹のような定理として剰余の定理があります.
剰余の定理は「多項式$f(x)$を1次式$x-a$で割ったときの余り」がすぐに求められる定理で,やはり剰余の定理もほとんど当たり前の定理です.
この記事では
- 因数定理の考え方と証明
- 因数定理の具体例
- 剰余の定理の考え方と証明
- 剰余の定理の具体例
を具体例とともに順に説明します.
「多項式」の一連の記事
因数定理の考え方と証明
まずは因数定理の考え方を説明し,定理の内容と証明を紹介します.
因数定理の考え方
多項式$f(x)$が
と因数分解できたとき,$x=1$のとき$x-1$が0となることから$f(1)=0$ですね.
同様に考えれば,次の[事実1]が成り立ちますね.
[事実1]$a$を定数とする.多項式$f(x)$が$x-a$を因数に持つとき,$f(a)=0$が成り立つ.
「多項式$f(x)$が$f(x)=(x-a)g(x)$($g(x)$は多項式)の形に因数分解できるとき,$f(a)=0$が成り立つ」と言っても同じことですね.
それでは,この逆は成り立つでしょうか.つまり,多項式$f(x)$が$f(a)=0$を満たすなら,$f(x)$は$x-a$を因数にもつでしょうか.
言い換えれば,多項式$f(x)$が$f(a)=0$を満たすにもかかわらず,$f(x)=(x-a)g(x)$($g(x)$は多項式)と表せないことはあるでしょうか.
このように考えると,$f(x)=(x-a)g(x)+b$($b\neq0$)となっていれば,$f(a)=0$とはならなさそうですから,逆も正しそうですね.
この[事実1]の逆を因数定理といいます.
因数定理の内容と証明
[因数定理]$a$を定数とする.多項式$f(x)$が$f(a)=0$を満たすとき,$f(x)$は$x-a$を因数にもつ.
一般に多項式を1次式で割った余りは定数なので,
とおける.すなわち,多項式$f(x)$を$x-a$で割った商を多項式$g(x)$,余りを定数$b$とおける.
このとき,仮定$f(a)=0$より
となって$b=0$を得る.よって,$f(x)=(x-a)g(x)$が成り立ち,$f(x)$は$x-a$を因数にもつ.
確かに,もし$f(x)=(x-a)g(x)+b$となる0でない実数$b$が存在すれば,$f(a)=0$となりませんから因数定理が成り立つことは成り立つことは当たり前に思えますね.
因数定理の具体例
具体的に3次多項式を因数定理を用いて因数分解してみましょう.
具体例1(${x^3-6x^2+11x-6}$)
$x^3-6x^2+11x-6$を因数分解せよ.
実際に$x$にいろいろ数を代入してみて,0となるような数$a$を見つけることができれば,因数定理から$x-a$を因数に持つことが分かります.
この場合は$x=1$で0となることが分かるので,因数定理から$x-1$を因数に持つことが分かります.
この3次式に$x=1$を代入すると
となるから,因数定理より$x^3-6x^2+11x-6$は$x-1$を因数にもつ.
$x^3+4x^2-5$を$x-1$で割ると,多項式の割り算の筆算より
なので,商は$x^2-5x-6$,余りは0である.すなわち,
が成り立つ.さらに,2次式$x^2-5x-6$は
と因数分解できるから,以上をまとめて
を得る.
因数定理から$x^3+4x^2-5$は$x-1$を因数にもつことが既に分かっているので,$x^3+4x^2-5$を$x-1$で割ったときの余りが0となるのは当たり前ですね.
具体例2(${3x^3-7x^2-7x+3}$)
次の問題も考え方は具体例1と全く同じで,実際に$x$に数を代入して$0$になるものを見つけましょう.
$3x^3-7x^2-7x+3$を因数分解せよ.
この3次式に$x=-1$を代入すると,
となるから,因数定理より$3x^3-7x^2-7x+3$は$x+1$を因数にもつ.
$3x^3-7x^2-7x+3$を$x+1$で割ると,多項式の割り算の筆算より
なので,商は$3x^2-10x+3$,余りは0である.すなわち,
が成り立つ.さらに,2次式$3x^2-10x+3$はたすきがけ因数分解より
と因数分解できるから,以上をまとめて
を得る.
剰余の定理の考え方と証明
次に剰余の定理の考え方を説明し,定理の内容と証明を紹介します.
剰余の定理の考え方と内容
多項式$f(x)$が
と変形できたとき,$x=1$のとき$x-1$が0となることから$f(1)=3$ですね.
同様に考えて成り立つ次の定理を剰余の定理と言います.
[剰余の定理]$a$を定数とする.多項式$f(x)$を$x-a$で割ったときの余りは$f(a)$である.
「多項式$f(x)$は$f(x)=(x-a)g(x)+f(a)$($g(x)$は多項式)の形に変形できる」と言っても同じことですね.
剰余の定理の証明
一般に多項式を1次式で割った余りは定数なので,
とおける.すなわち,$f(x)$を$x-a$で割った商を$g(x)$,余りを$b$とおける.
このとき,
となって$f(a)=b$を得る.よって,$f(x)$を$x-a$で割ったときの余りは$b$である.
剰余の定理の具体例
多項式を1次式で割ったときの余りは,剰余の定理から一発で求まります.
具体例1($x^3-6x^2+4x+3$を$x-5$で割った余り)
$x^3-6x^2+4x+3$を$x-5$で割った余りを求めよ.
剰余の定理より,求める余りは$x^3-6x^2+4x+3$に$x=5$を代入したものに等しく
である.
剰余の定理を使わなくても,実際に$x^3-6x^2-4x+3$を$x-5$で割って
としても余りが$-2$であることは分かりますが,剰余の定理を使う方がよっぽど楽ですね.
具体例2(${3x^4-4x^2-2x+7}$を$x-2$で割った余り)
次の問題も「多項式を1次式で割った余り」なので,具体例1と同様に解けますね.
$3x^4-4x^2-2x+7$を$x-2$で割った余りを求めよ.
剰余の定理より,求める余りは$3x^4-4x^2-2x+7$に$x=2$を代入したものに等しく
である.
発展(因数定理と剰余の定理の関係)
この記事では因数定理と剰余の定理を別々に証明しました.しかし,実は
- 因数定理を用いて剰余の定理を示す
- 剰余の定理を用いて因数定理を示す
ということができます.つまり,剰余の定理と因数定理は本質的に同じ定理ということになります.
因数定理を用いた剰余の定理の証明
剰余の定理を因数定理から証明してみましょう.
[剰余の定理(再掲)]$a$を定数とする.多項式$f(x)$を$x-a$で割ったときの余りは$f(a)$である.
多項式$f(x)-f(a)$に$x=a$を代入すると0となるから因数定理より,多項式$g(x)$を用いて$f(x)-f(a)=(x-a)g(x)$と表せる.
よって,$f(a)$を移項して$f(x)=(x-a)g(x)+f(a)$となるから,$f(x)$を$x-a$で割った余りは$f(a)$である.
$f(x)-f(a)$が$x=a$で0になることから,因数定理が適用できるわけですね.
剰余の定理を用いた因数定理の証明
因数定理から剰余の定理を証明してみましょう.
[因数定理(再掲)]$a$を定数とする.多項式$f(x)$が$f(a)=0$を満たすとき,$f(x)$は$x-a$を因数にもつ.
剰余の定理より多項式$f(x)$は多項式$g(x)$を用いて$f(x)=(x-a)g(x)+f(a)$と表せる.
仮定$f(a)=0$より$f(x)=(x-a)g(x)$となるから,$f(x)$は$x-a$を因数にもつ.
因数定理は剰余の定理の余りが0の場合に相当するというわけですね.
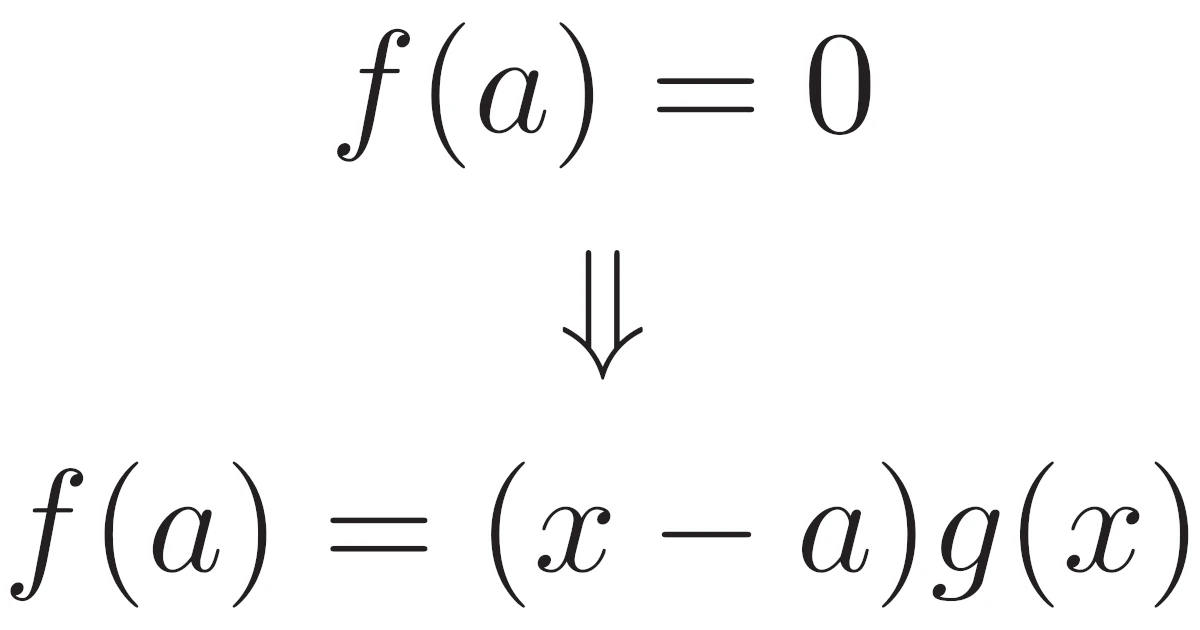
コメント