漸化式の基本２｜漸化式の基本の[等差数列]と[等比数列]

前回の記事で説明したように，数列$\{a_n\}$に対して

$\begin{align*} a_{n+1}=a_n+2n \end{align*}$

のような項同士の関係式を漸化式といい，漸化式から一般項$a_n$を求めることを漸化式を解くというのでした．

漸化式はいつでも簡単に解けるとは限りませんが，簡単に解ける漸化式として

等差数列の漸化式
等比数列の漸化式

は他の解ける漸化式のベースになることが多く，確実に押さえておくことが大切です．

この記事では，この２タイプの漸化式「等差数列の漸化式」と「等比数列の漸化式」を説明します．

一連の記事はこちら

【漸化式の基本１｜漸化式とは？漸化式の考え方を例から解説！】
【漸化式の基本２｜漸化式の基本の[等差数列]と[等比数列]】←今の記事
【漸化式の基本３｜数学的帰納法はイメージは「ドミノ倒し」！】

等差数列の漸化式
等比数列の漸化式
具体例

等差数列の漸化式

まず，等差数列を復習しましょう．

１つ次の項に移るごとに，同じ数が足されている数列を等差数列という．また，このときに１つ次の項に移るごとに足されている数を公差という．

この定義から，例えば公差３の等差数列$\{a_n\}$は

$a_2=a_1+3$
$a_3=a_2+3$
$a_4=a_3+3$
……

となっていますから，これらをまとめると

$\begin{align*} a_{n+1}=a_n+3\quad (n=1,2,3,\dots) \end{align*}$

と表せます．もちろん，逆にこの漸化式をもつ数列$\{a_n\}$は公差３の等差数列ですね．

公差を一般に$d$としても同じことですから，一般に次が成り立つことが分かります．

[等差数列]　$d$を定数とする．このとき，数列$\{a_n\}$について，次は同値である．

漸化式$a_{n+1}=a_n+d$が成り立つ．
数列$\{a_n\}$は公差$d$の等差数列である．

さて，公差$d$の等差数列$\{a_n\}$の一般項は

$\begin{align*} a_{n}=a_1+(n-1)d\quad\dots(*) \end{align*}$

でしたから，今みた定理と併せて漸化式$a_{n+1}=a_n+d$は$(*)$と解けることになりますね．

数列１
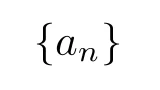
最初の一歩は等差数列と等比数列！

高校数学での数列で基礎となるのは「等差数列」と「等比数列」で，少し複雑な数列も等差数列または等比数列に帰着させることが多いです．この記事では，数列の基礎と等差数列・等比数列を説明します．

等比数列の漸化式

まず，等差数列を復習しましょう．

１つ次の項に移るごとに，同じ数がかけられている数列を等比数列という．また，このときに１つ次の項に移るごとにかけられている数を公比という．

等比数列の漸化式についても，等差数列と並行に話を進めることができます．

この定義から，例えば公比３の等比数列$\{b_n\}$は

$b_2=3b_1$
$b_3=3b_2$
$b_4=3b_3$
……

となっていますから，これらをまとめると

$\begin{align*} b_{n+1}=3b_n\quad (n=1,2,3,\dots) \end{align*}$

と表せます．もちろん，逆にこの漸化式をもつ数列$\{b_n\}$は公比３の等差数列ですね．

公比を一般に$r$としても同じことですから，一般に次が成り立つことが分かります．

[等比数列]　$r$を定数とする．このとき，数列$\{b_n\}$について，次は同値である．

漸化式$b_{n+1}=rb_n$が成り立つ．
数列$\{b_n\}$は公比$r$の等比数列である．

さて，公比$d$の等比数列$\{a_n\}$の一般項は

$\begin{align*} a_{n}=a_1r^{n-1}\quad\dots(**) \end{align*}$

でしたから，今みた定理と併せて漸化式$b_{n+1}=rb_n$は$(**)$と解けることになりますね．

数列１
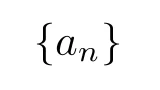
最初の一歩は等差数列と等比数列！

具体例

それでは具体例を考えましょう．

$a_1=1$を満たす数列$\{a_n\}$に対して，次の漸化式を解け．

$a_{n+1}=a_n+2$
$a_{n+1}=a_n-\frac{3}{2}$
$a_{n+1}=2a_n$
$a_{n+1}=-a_n$

ただ公式を適用しようとするのではなく，それぞれの漸化式を見て意味を考えることが大切です．

２を加えて次の項に移っているから公差２の等差数列
$-\frac{3}{2}$を加えて次の項に移っているから公差$-\frac{3}{2}$の等差数列
２をかけて次の項に移っているから公比２の等比数列
$-1$をかけて次の項に移っているから公比$-1$の等比数列

と考えれば，初項が$a_1=1$であることから直ちに漸化式を解くことができますね．

(1)　漸化式$a_{n+1}=a_n+2$より数列$\{a_n\}$は公差２の等差数列だから，一般項$a_n$は初項$a_1$に公差２を$n-1$回加えたものである．

よって，一般項$a_n$は

$\begin{align*} a_n =&a_1+2(n-1) \\=&1+2(n-1) \\=&2n-1 \end{align*}$

である．

(2)　漸化式$a_{n+1}=a_n-\frac{3}{2}$より公差$-\frac{3}{2}$の等差数列だから，一般項$a_n$は初項$a_1$に公差$-\frac{3}{2}$を$n-1$回加えたものである．

よって，一般項$a_n$は

$\begin{align*} a_n =&a_1-\frac{3}{2}(n-1) \\=&1-\frac{3}{2}(n-1) \\=&-\frac{3}{2}n+\frac{5}{2} \end{align*}$

である．

(3)　漸化式$a_{n+1}=2a_n$より公比２の等比数列だから，一般項$a_n$は初項$a_1$に公比２を$n-1$回かけたものである．

よって，一般項$a_n$は

$\begin{align*} a_n =&2^{n-1}a_1 \\=&2^{n-1}\cdot1 \\=&2^{n-1} \end{align*}$

である．

(4)　漸化式$a_{n+1}=-a_n$より公比$-1$の等比数列だから，一般項$a_n$は初項$a_1$に公比$-1$を$n-1$回かけたものである．

よって，一般項$a_n$は

$\begin{align*} a_n =&(-1)^{n-1}a_1 \\=&(-1)^{n-1}\cdot1 \\=&(-1)^{n-1} \end{align*}$

である．

次の記事では，証明で重要な手法である数学的帰納法について説明します．