数学的帰納法は「任意の自然数$n$に対して,〜が成り立つことを示せ.」というタイプの証明問題に対して威力を発揮することが多い証明法です.
大学受験では数学的帰納法は背理法と並んで頻出で,確実に理解しておきたい証明法です.
数学的帰納法は慣れてしまえばそう難しくない論法なので,実際に問題を解くにつれてだんだん腑に落ちてくる人は多いようです.
そこで,この記事では
- 数学的帰納法の仕組み・具体例
- 数学的帰納法の発展形
を順に説明します.
「数列」の一連の記事
数学的帰納法の直感的な仕組みと具体例
冒頭の繰り返しになりますが,数学的帰納法は「任意の自然数$n$に対して,〜が成り立つことを示せ.」という問題に有効なことが多いです.
直感的な仕組み
数学的帰納法は次の2つを示すことで証明する論法です.
- $n=1$のときに成り立つことを示す
- 「$n=k$のときに成り立つ」と仮定すると,$n=k+1$のときにも成り立つことを示す
この数学的帰納法は「ドミノ倒し」に例えることができます.
つまり,(1)は「最初のピースを倒す」ということに相当し,(2)は「$k$個目のピースが倒れると,$k+1$個目のピースも倒れる」ということに相当します.
つまり,(1), (2)がどちらも証明できれば
- (1)より$n=1$のときが成り立つ.
- $n=1$が成り立つから,(2)より$n=2$のときが成り立つ.
- $n=2$が成り立つから,(2)より$n=3$のときが成り立つ.
- $n=3$が成り立つから,(2)より$n=4$のときが成り立つ.
- ……
と続いていくので,任意の自然数$n$に対して成り立つことが証明できたことになるわけです.
もし(1)が言えないと「最初のピースが倒せない」し,(2)が言えないと「$k$個目が倒れても,$k+1$個目が倒れてくれないかもしれない」ので,(1), (2)のどちらが欠けても数学的帰納法は成り立ちませんね.
以下,具体例を考えましょう.
具体例1(等式の証明)
任意の自然数$n$に対して,等式$1+3+5+\dots+(2n-1)=n^2$が成り立つことを示せ.
素直に数学的帰納法の手順に当てはめると
- $n=1$のときに$1+3+5+\dots+(2n-1)=n^2$が成り立つことを示す.
- $1+3+5+\dots+(2k-1)=k^2$ ($k$は自然数)が成り立つと仮定すると,$1+3+5+\dots+\{2(k+1)-1\}=(k+1)^2$が成り立つことを示す.
の2つを示せば良いですね.
数学的帰納法により示す.
[1]$n=1$のとき
- $1+3+5+\dots+(2n-1)=1$($n=1$より1項目のみ)
- $n^2=1^2=1$
なので,確かにこれらは等しいから等式$1+3+5+\dots+(2n-1)=n^2$が成り立つ.
[2]「$n=k$のとき$1+3+5+\dots+(2n-1)=n^2$が成り立つ」と仮定する.すなわち,$1+3+5+\dots+(2k-1)=k^2$が成り立つと仮定する.
このとき,
だから,$n=k+1$のときにも等式$1+3+5+\dots+(2n-1)=n^2$が成り立つことが示された.
[1]と[2]より,任意の自然数$n$に対して,等式$1+3+5+\dots+(2n-1)=n^2$が成り立つことが分かった.
この例のように,数学的帰納法では最初の部分(今の例の[1])はすぐに分かることが多いです.
また,帰納的な部分(今の例の[2])は$n=k$の場合を用いて$n=k+1$を示せばよいわけですね.
具体例2(不等式の証明)
不等式の証明ですが,やはり「任意の自然数$n$に対して,〜が成り立つことを示せ.」というタイプの証明なので,数学的帰納法が第1感です.
数学的帰納法により示す.
[1]$n=1$のとき,
- $a_n=a_1=1$
- $a_{n+1}=a_2=\sqrt{a_1+2}=\sqrt{3}$
なので,確かに不等式$a_n<a_{n+1}$が成り立つ.
[2]「$n=k$のとき$a_n<a_{n+1}$が成り立つ」と仮定する.すなわち,$a_{k}<a_{k+1}$が成り立つと仮定する.
このとき,漸化式より$a_{k+2}=\sqrt{a_{k+1}+2}$, $a_{k+1}=\sqrt{a_k+2}$なので,
である.帰納法の仮定$a_{k}<a_{k+1}$より$\sqrt{a_{k+1}+2}-\sqrt{a_k+2}>0$なので,$a_{k+2}-a_{k+1}>0$が成り立つ.
すなわち,$a_{k+1}<a_{k+2}$が成り立つ.
よって,$n=k+1$のときにも不等式$a_{n}<a_{n+1}$が成り立つことが示された.
[1]と[2]より,任意の自然数$n$に対して,不等式$a_{n}<a_{n+1}$が成り立つことが分かった.
「任意の自然数$n$に対して,不等式$a_{n}<a_{n+1}$が成り立つ」というのは,「数列$\{a_n\}$が単調増加」と言い換えられますね.
このように,数列$\{a_n\}$の単調性を示す際に数学的帰納法が有効なことは多いです.
具体例3(予想の正当化)
「任意の自然数$n$に対して,〜が成り立つことを示せ.」というタイプの証明ではありませんが,この問題も数学的帰納法により解くことができます.
$a_1=1$と漸化式から実際に$a_2,a_3,a_4$を求めていくと,
となります.このことから「任意の自然数$n$に対して,$a_n=\dfrac{1}{n}$が成り立つこと」が予想できます.
そこで,この予想が正しいことを数学的帰納法により示し,一般項が$a_n=\dfrac{1}{n}$であることを正当化しましょう.
$a_1=1$, $a_{n+1}=\dfrac{a_n}{1+a_n}$だから
だから,数列$\{a_n\}$の一般項は$a_n=\dfrac{1}{n}$と予想できる.これを数学的帰納法により示す.
[1]$n=1$のとき,
- $a_n=a_1=1$
- $\dfrac{1}{n}=\dfrac{1}{1}=1$
なので,確かに不等式$a_n=\dfrac{1}{n}$が成り立つ.
[2]「$n=k$のとき$a_n=\dfrac{1}{n}$が成り立つ」と仮定する.すなわち,$a_k=\dfrac{1}{k}$が成り立つと仮定する.
このとき,漸化式より$a_{k+1}=\dfrac{a_k}{1+a_k}$なので,
となって,$n=k+1$のときにも$a_n=\dfrac{1}{n}$が成り立つことが示された.
[1]と[2]より,数列$\{a_n\}$の一般項が$a_n=\dfrac{1}{n}$であることが分かった.
この具体例のように「一般項を実験して予想し,予想を数学的帰納法により示す」という問題は頻出なので,しっかりフォローしておきましょう.
数学的帰納法の発展形
いまみた3つの具体例はいずれも
- $n=1$のときに成り立つことを示す
- 「$n=k$のときに成り立つ」と仮定すると,$n=k+1$のときにも成り立つことを示す
という最も基本的な数学的帰納法でした.
これを少し発展させた次のタイプの帰納法もよく用いられます.
具体例4(最初が${n=1}$ではないタイプ)
4以上の任意の自然数$n$に対して,不等式$n!>2^n$が成り立つことを示せ.
$n!$はどんどん大きな自然数をかけていく一方で,$2^n$はずっと$2$をかけていくものなので,十分大きな$n$に対しては$n!$の方が大きくなります.
それが$n\geqq4$で成り立つということを示す問題なわけですね.
数学的帰納法の仕組みが理解できていれば,この場合は
- $n=4$のときに成り立つことを示す
- 「$n=k$のときに成り立つ」と仮定すると,$n=k+1$のときにも成り立つことを示す
という数学的帰納法で示せることが分かりますね.
数学的帰納法により示す.
[1]$n=4$のとき,
- $4!=24$
- $2^4=16$
なので,確かに不等式$n!>2^n$が成り立つ.
[2]「$n=k$ ($k\ge4$)のとき$n!>2^n$が成り立つ」と仮定する.すなわち,$k!>2^{k}$が成り立つと仮定する.
このとき,
である.ただし,最後の不等式では$k\ge4$であることに注意.
よって,$(k+1)!>2^{k+1}$が成り立つから,$n=k+1$のときにも不等式$n!>2^n$が成り立つことが示された.
[1]と[2]より,$4$以上の任意の自然数$n$に対して,不等式$n!>2^n$が成り立つことが分かった.
具体例5(2つ以上前も仮定するタイプ)
具体例3と同様に,「一般項を予想して数学的帰納法により予想が正しいことを示す」という方法で解ける問題ですが,今回は数列の漸化式が3項間漸化式なので$a_n$と$a_{n+1}$の情報から$a_{n+2}$が定まります.
このことから,数学的帰納法で帰納的な部分では1つ前の仮定だけではなく,2つ前の仮定も必要となります.
$a_1=1$, $a_2=-1$, $a_{n+2}=2a_{n}+a_{n+1}$だから
だから,数列$\{a_n\}$の一般項は$a_n=(-1)^{n+1}$と予想できる.これを数学的帰納法により示す.
[1]$n=1$のとき,
- $a_n=a_1=1$
- $(-1)^{n+1}=(-1)^2=1$
なので,確かに不等式$a_n=(-1)^{n+1}$が成り立つ.
[2]$n=2$のとき,
- $a_n=a_2=-1$
- $(-1)^{n+1}=(-1)^3=-1$
なので,確かに不等式$a_n=(-1)^{n+1}$が成り立つ.
[3]「$n=k,k+1$のとき$a_n=(-1)^{n+1}$が成り立つ」と仮定する.すなわち,$a_k=(-1)^{k+1}$, $a_{k+1}=(-1)^{k+2}$が成り立つと仮定する.
このとき,漸化式より$a_{k+2}=2a_{k}+a_{k+1}$なので,
となって,$n=k+1$のときにも$a_n=(-1)^{n+1}$が成り立つことが示された.
[1]〜[3]より,数列$\{a_n\}$の一般項が$a_n=(-1)^{n+1}$であることが分かった.
1つ前のみを仮定する帰納法を「昨日帰納法」,1つ前と2つ前を仮定する帰納法を「昨日一昨日帰納法」と(ダジャレ的に)表現することもありますが,正式な名前ではないので答案で書くのは避けた方が良いでしょう.
例えば$n=3$の場合は$n=1,2$の2つから決まるので,[1]と[2]の2つを最初に考えておく必要がありますね.
また,問題によっては3つ前から仮定する場合や,それまでのすべて($n=1,2,\dots,k$の全て)を仮定する問題もあります.
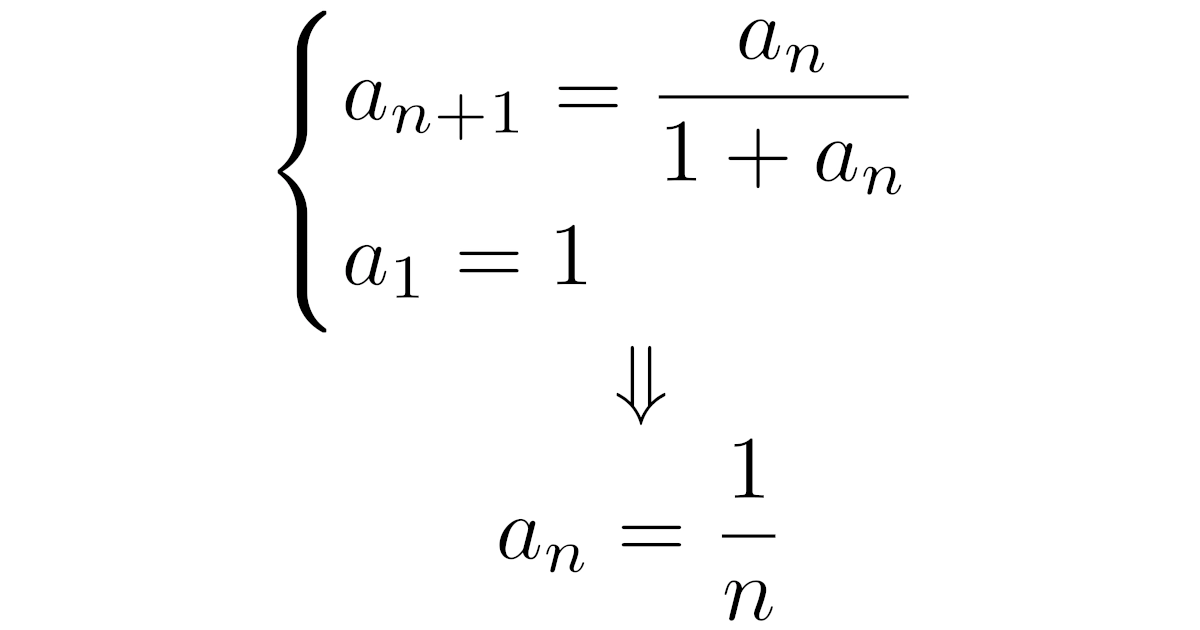
コメント