例えば，和
\begin{align*}\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\dots+\frac{1}{(n-1)n}\end{align*}
は部分分数分解を用いることで簡単な形に計算することができます．
部分分数分解は数学IIIの積分でも必要になるので，数学IIIが必要な人はここでしっかり理解しておきましょう．
また，部分分数分解の公式を丸覚えしている人がいますが，考え方から理解していれば覚えていなくてもすぐに導けます．
この記事では，
- 部分分数分解の公式
- 部分分数分解を用いた数列の和
を順に解説します．
「数列」の一連の記事
部分分数分解の公式
部分分数分解とは「１つの分数を複数の分数の和（もしくは差）に分けること」を言います．
たとえば，$\dfrac{1}{6}$は
\begin{align*}\frac{1}{6}=\frac{1}{2}-\frac{1}{3}\end{align*}
と２つの分数に分けることができますし，$\dfrac{1}{15}$も
\begin{align*}\frac{1}{15}=\frac{1}{2}\bra{\frac{1}{3}-\frac{1}{5}}\end{align*}
と２つの分数に分けることができます．これらを一般化すると次のようになります．
実数$a,b$が$a\neq b$であるとき，任意の実数$k$に対して等式
\begin{align*}\frac{1}{(k+a)(k+b)}=\frac{1}{b-a}\bra{\frac{1}{k+a}-\frac{1}{k+b}}\end{align*}
が成り立つ．
こ$\dfrac{1}{(k+a)(k+b)}$を通分する前の$\dfrac{1}{k+a}$と$\dfrac{1}{k+b}$に分けたいときに使えますね．
証明は簡単で，右辺を通分すれば左辺になることが確かめられます．
$\dfrac{1}{k+a}-\dfrac{1}{k+b}$を通分すると
\begin{align*}\frac{1}{k+a}-\frac{1}{k+b}
=&\frac{(k+b)-(k+a)}{(k+a)(k+b)}
\\=&\frac{b-a}{(k+a)(k+b)}\end{align*}
である．こうして得られた$\dfrac{1}{k+a}-\dfrac{1}{k+b}=\dfrac{b-a}{(k+a)(k+b)}$の両辺を$b-a$で割って，
\begin{align*}\frac{1}{b-a}\bra{\frac{1}{k+a}-\frac{1}{k+b}}=\frac{1}{(k+a)(k+b)}\end{align*}
を得る．
$\dfrac{1}{k+a}$から$\dfrac{1}{k+b}$を引くと，通分したときに分子で$k$と$-k$が出てきて打ち消し合うのがポイントですね．
つまり，先に
\begin{align*}\frac{1}{(k+a)(k+b)}=\frac{1}{\qquad\qquad}\bra{\frac{1}{k+a}-\frac{1}{k+b}}\end{align*}
の雛型を用意しておいて，右辺を通分して分子に現れる$b-a$を打ち消して両辺の辻褄を合わせるために$\dfrac{1}{b-a}$を右辺の前に置けばよいですね．
こう考えれば公式を覚える必要が全くないことが分かりますね．
部分分数分解を用いた数列の和
部分分数分解を用いて，数列の和を計算してみましょう．
具体例１
和$\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dots+\dfrac{1}{(n-1)n}$を計算せよ．
各項$\dfrac{1}{k(k+1)}$（$k=1,2,\dots,n$）は
\begin{align*}\frac{1}{k(k+1)}=\frac{1}{k}-\frac{1}{k+1}\end{align*}
と部分分数分解できる（上の部分分数分解の公式で$a=0$, $b=1$の場合）．
よって，$k=1,2,\dots,n$を代入して足し合わせて
\begin{align*}&\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\dots+\frac{1}{(n-1)n}
\\=&\bra{\frac{1}{1}-\frac{1}{2}}+\bra{\frac{1}{2}-\frac{1}{3}}+\bra{\frac{1}{3}-\frac{1}{4}}+\dots+\bra{\frac{1}{n}-\frac{1}{n+1}}
\\=&1+\bra{-\frac{1}{2}+\frac{1}{2}}+\bra{-\frac{1}{3}+\frac{1}{3}}+\dots+\bra{-\frac{1}{n}+\frac{1}{n}}-\frac{1}{n+1}
\\=&1-\frac{1}{n+1}
=\frac{n}{n+1}\end{align*}
と計算できる．
最後から２番目の等号でプラスマイナスがバサバサ消えているのが分かりますね．
具体例２
和$\dfrac{1}{1\cdot3}+\dfrac{1}{2\cdot4}+\dots+\dfrac{1}{n(n+2)}$を計算せよ．
各項$\dfrac{1}{k(k+2)}$（$k=1,2,\dots,n$）は
\begin{align*}\frac{1}{k(k+2)}=\frac{1}{2}\bra{\frac{1}{k}-\frac{1}{k+2}}\end{align*}
と部分分数分解できる（上の部分分数分解の公式で$a=0$, $b=2$の場合）．
よって，$k=1,2,\dots,n$を代入して足し合わせて
\begin{align*}&\frac{1}{1\cdot3}+\frac{1}{2\cdot4}+\dots+\frac{1}{n(n+2)}
\\=&\frac{1}{2}\brb{\bra{1-\frac{1}{3}}+\bra{\frac{1}{2}-\frac{1}{4}}+\bra{\frac{1}{3}-\frac{1}{5}}+\dots+\bra{\frac{1}{n}-\frac{1}{n+2}}}
\\=&\frac{1}{2}\bra{1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}}
\\=&\frac{1}{2}\cdot\frac{3(n+1)(n+2)-2(n+2)-2(n+1)}{2(n+1)(n+2)}
\\=&\frac{1}{2}\cdot\frac{3n^2+5n}{2(n+1)(n+2)}
=\frac{n(3n+5)}{4(n+1)(n+2)}\end{align*}
と計算できる．
例１と同じく同じものがプラスマイナスでバサバサ消えますが，プラスとマイナスが２つずれているので４項残ってくることに注意してください．
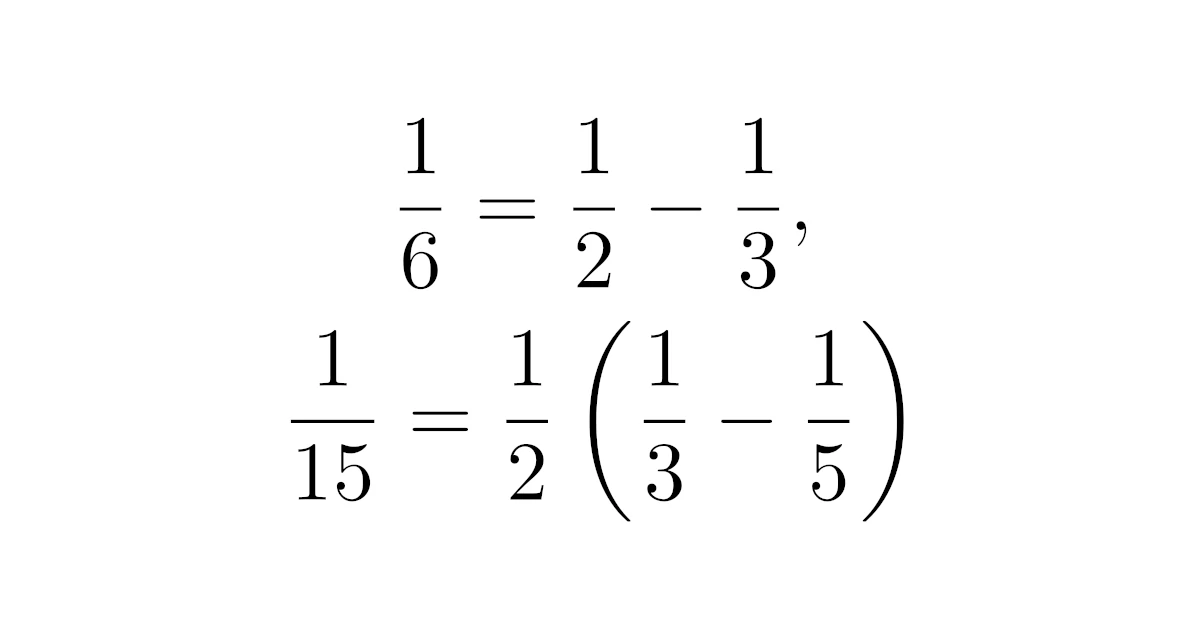
コメント