2017年度｜京都大学｜理系数学｜入試の解答例と考え方

2017年度の京都大学の前期入試の理系数学を全問（問１〜問６）解説します．

各問を考え方から解説しています．

「大学入試数学解説」の一連の記事

京都大学

第１問

開く問題の表示/非表示

$w$を0でない複素数，$x,y$を$w+\dfrac{1}{w}=x+yi$を満たす実数とする．

実数$R$は$R>1$を満たす実数とする．$w$が絶対値$R$の複素数全体を動くとき，$xy$平面上の点$(x,y)$の軌跡を求めよ．
実数$\alpha$は$0<\alpha<\dfrac{\pi}{2}$を満たす実数とする．$w$が偏角$\alpha$の複素数全体を動くとき，$xy$平面上の点$(x,y)$の軌跡を求めよ．

複素数と図形と方程式の複合問題です．

解答への筋道

偏角や絶対値の情報が与えられていることから，(1)も(2)も$w$を極形式でおくことは瞬時に見えたい問題です．$R$や$\alpha$が定数であることに注意してください．

問題の捉え方

(1)と(2)で異なる点は

$w$の絶対値$R$が与えられている
$w$の偏角$\alpha$が与えられている

という点ですね．

これら$R$, $\alpha$は定数なので，(1)で$w$は複素平面上で半径$R$の円周上を動き，(2)で$w$は複素平面上で偏角$\alpha$の直線上を動くわけですね．

それぞれの場合で$w$を動かして，$w+\dfrac{1}{w}=x+yi$で定まる点$(x,y)$がどのような軌跡を描くのかを問われているわけですね．

軌跡

軌跡で重要なことは「軌跡は動かないところは除外して答えなければならない」というところです．

つまり，とくに(2)では単に媒介変数を消去しただけでは軌跡になっていないことに注意が必要です．

実際，(2)では$w$が偏角$\alpha$を保って動くので$w=r(\cos{\alpha}+i\sin{\alpha})$（$r>0$）と表すと，$w+\dfrac{1}{w}=x+yi$から

$\begin{align*}\begin{cases} x=\bra{r+\frac{1}{r}}\cos\alpha\\ y=\bra{r-\frac{1}{r}}\sin\alpha \end{cases}\dots(*)\end{align*}$

という$r$を媒介変数とした$x,y$の関係式が得られます．ここから$r$を消去すると双曲線

$\begin{align*}1=\frac{x^2}{(2\cos\alpha)^2}-\frac{y^2}{(2\sin\alpha)^2}\end{align*}$

が得られますが，$x$が負の値を取らないため双曲線の片側しか動かないので，これを軌跡としてはいけません．

このように，軌跡の問題では通らない点を除外して答えなければなりません．

(2)の概形

いま(2)では「$x$が負の値を取らない」と説明しましたが，このことは(2)の軌跡の概形が予想できないと難しいかもしれません．

(2)で$w=r(\cos{\alpha}+i\sin{\alpha)}$とするとき，$r$が大きいときには$\dfrac{1}{w}\approx0$なので，$w+\dfrac{1}{w}=x+yi$と併せて$w\approx x+yi$となります．

よって，$x\approx r\cos{\alpha}$, $y\approx r\sin{\alpha}$なので$y\approx\tan{\alpha}x$となり，$r\to\infty$で$y=(\tan{\alpha})x$（$x\geqq0$）を漸近線にもつことがみてとれます．

一方，$r$が$0$に近いときには$w\approx0$なので，同様に$\dfrac{1}{w}\approx x+yi$より$x\approx\dfrac{1}{r}\cos{\alpha}$, $y\approx-\dfrac{1}{r}\sin{\alpha}$なので，$r\to+0$で$y=-(\tan{\alpha})x$（$x\geqq0$）を漸近線にもつこともみてとれますね．

解答例

(1)　$w=R(\cos{\theta}+i\sin{\theta})$（$0\leqq\theta<2\pi$）とおける．ド・モアブルの定理から

$\begin{align*}\frac{1}{w} &=\frac{1}{R}\{\cos(-\theta)+i\sin(-\theta)\} \\&=\frac{1}{R}(\cos\theta-i\sin\theta)\end{align*}$

だから，与えられた等式は

$\begin{align*}&w+\dfrac{1}{w}=x+iy \\&\iff\bra{R+\frac{1}{R}}\cos\theta+i\bra{R-\frac{1}{R}}\sin\theta=x+iy \\&\iff\begin{cases}x=\bra{R+\frac{1}{R}}\cos\theta\\ y=\bra{R-\frac{1}{R}}\sin\theta\end{cases}\end{align*}$

となる．$R>1$より$R\pm\frac{1}{R}\neq0$だから，これは楕円

$\begin{align*}1=\frac{x^2}{\bra{R+\frac{1}{R}}^2}+\frac{y^2}{\bra{R-\frac{1}{R}}^2}\end{align*}$

の媒介変数表示である．すなわち，求める軌跡は長軸は$x$軸，短軸は$y$軸上にあり，長径$2R+\dfrac{2}{R}$，短径$2R-\dfrac{2}{R}$の楕円である．

Rendered by QuickLaTeX.com

(2) $w=r(\cos\alpha+i\sin\alpha)$とおける．ただし，$0<r$とする．(1)と同様にして，

$\begin{align*}\begin{cases} x=\bra{r+\frac{1}{r}}\cos\alpha\\ y=\bra{r-\frac{1}{r}}\sin\alpha \end{cases}\dots(*)\end{align*}$

を得る．$0<\alpha<\dfrac{\pi}{2}$より$\cos\alpha\neq0$, $\sin\alpha\neq0$なので，

$\begin{align*}(*) &\iff\begin{cases} x\sin{\alpha}=\bra{r+\frac{1}{r}}\sin{\alpha}\cos{\alpha}\\ y\cos{\alpha}=\bra{r-\frac{1}{r}}\sin{\alpha}\cos{\alpha} \end{cases} \\&\iff\begin{cases} x\sin{\alpha}+y\cos{\alpha}=2r\sin{\alpha}\cos{\alpha}\\ x\sin{\alpha}-y\cos{\alpha}=\frac{2}{r}\sin{\alpha}\cos{\alpha} \end{cases}\end{align*}$

となって，この２式の辺々をかけると

$\begin{align*}&x^2\sin^2{\alpha}-y^2\cos^2{\alpha}=4\sin^2{\alpha}\cos^2{\alpha} \\&\iff1=\frac{x^2}{(2\cos\alpha)^2}-\frac{y^2}{(2\sin\alpha)^2}\quad\dots[1]\end{align*}$

が得られる．また，相加平均と相乗平均の関係から，

$\begin{align*}\frac{x}{\cos\alpha}=r+\frac{1}{r}\geqq2\sqrt{r\cdot\frac{1}{r}}=2\end{align*}$

だから，$x\geqq2\cos\alpha\dots[2]$である．

Rendered by QuickLaTeX.com

逆に，[1]かつ[2]を満たす$x,y$を考える．$r-\dfrac{1}{r}$は$r>0$で実数全体を動くから，

$\begin{align*}&\frac{y}{\sin{\alpha}}=r-\frac{1}{r} \iff y=\bra{r-\frac{1}{r}}\sin{\alpha}\end{align*}$

なる$r$が存在する．よって，[1]から

$\begin{align*}\frac{x^2}{(2\cos\alpha)^2} &=1+\brb{\frac{1}{2}\bra{r-\frac{1}{r}}}^2 \\&=r^2+\frac{1}{4}\bra{r^2-2+\frac{1}{r^2}} \\&=\frac{1}{4}\bra{r^2+2+\frac{1}{r^2}} \\&=\brb{\frac{1}{2}\bra{r+\frac{1}{r}}}^2\end{align*}$

が成り立つ．[2]より$\dfrac{x}{2\cos{\alpha}}>0$なので，

$\begin{align*}\frac{x}{2\cos\alpha}=\frac{r+\frac{1}{r}}{2} \iff x=\bra{r+\frac{1}{r}}\cos\alpha\end{align*}$

となる．よって，[1]かつ[2]から$(*)$が得られることが分かった．

以上より，求める軌跡は[1]かつ[2]なので，

$\begin{align*}1=\frac{x^2}{(2\cos\alpha)^2}-\frac{y^2}{(2\sin\alpha)^2}\quad(x\geqq2)\end{align*}$

である．

第２問

開く問題の表示/非表示

四面体$\mrm{OABC}$を考える．点$\mrm{D},\mrm{E},\mrm{F},\mrm{G},\mrm{H},\mrm{I}$は，それぞれ辺$\mrm{OA},\mrm{AB},\mrm{BC},\mrm{CO},\mrm{OB},\mrm{AC}$上にあり，頂点ではないとする．このとき，次の問に答えよ．

$\Ve{DG}$と$\Ve{EF}$が平行ならば，$\mrm{AE}:\mrm{EB}=\mrm{CF}:\mrm{FB}$であることを示せ．
$\mrm{D},\mrm{E},\mrm{F},\mrm{G},\mrm{H},\mrm{I}$が正八面体の頂点となっているとき，これらの点は$\mrm{OABC}$の各辺の中点であり，$\mrm{OABC}$は正四面体であることを示せ．

京都大学は四面体の問題をよく出題しますが，本問も四面体の空間図形の問題ですね．

解答への筋道

(1)は空間における平面と直線の平行，(2)は正八面体という条件と(1)を利用する問題です．

問題の捉え方

図は以下のようになっています．

辺上の点$\mrm{D},\mrm{E},\mrm{F},\mrm{G},\mrm{H},\mrm{I}$が動くイメージですね．

(1)では比例式$\mrm{AE}:\mrm{EB}=\mrm{CF}:\mrm{FB}$を示す問題なので相似を利用したいというのが第１感です．

そう考えると$\tri{BAC}$と$\tri{BEF}$が相似であることを示せば良さそうですね．

(2)では正八面体という条件から，対称性を考えて辺上の点$\mrm{D},\mrm{E},\mrm{F},\mrm{G},\mrm{H},\mrm{I}$は全て中点となりそうですね．

よって，三角形の相似から例えば$2\mrm{IF}=\mrm{AB}$が成り立ちます．このように，他の四面体$\mrm{OABC}$の辺の長さも正八面体の辺の長さの比が$2:1$であることが分かり，四面体$\mrm{OABC}$が正四面体であることが従います．

空間上の平行性

(1)では$\tri{BAC}$と$\tri{BEF}$が相似であることを示せば良さそうで，このためには「$\Ve{DG}$と$\Ve{EF}$が平行」という条件から「$\mrm{EF}$と$\mrm{AC}$が平行」であることを示しにいくことになりそうです．

このために

空間上の平面と直線の平行性
空間上の直線と直線の平行性

の定義を確認しておきましょう．

空間上の平面$\alpha$と直線$\ell$が平行であるとは，$\alpha$と$\ell$が共有点をもたないことをいう．

空間上の直線$\ell_1$と直線$\ell_2$が平行であるとは，$\ell_1$と$\ell_2$が同一平面上に存在し，共有点をもたないことをいう．

このことから，空間上の平面$\alpha$と直線$\ell$が平行でなければ，直線$\ell$は平面$\alpha$上の任意の直線$m$と平行ではありませんね．

よって，「直線$\mrm{AC}$と直線$\mrm{EF}$が平行でない」と仮定する背理法を用いると，直線$\mrm{AC}$と直線$\mrm{EF}$は交点をもつことになり，平面$\mrm{OAC}$と直線$\mrm{EF}$は交点をもちますね．

よって，平面$\mrm{OAC}$と直線$\mrm{EF}$は平行でないので，「$\Ve{DG}$と$\Ve{EF}$が平行」という条件に矛盾します．

なお，背理法を使おうと思った理由は否定の証明は背理法が有効なことが多いためです．

つまり，平行の定義が「共有点をもたない」と否定なので，平行であることを示すには「平行でない」と仮定して「共有点をもつ」という条件で考える方が扱いやすいためです．

このように「否定の証明は背理法」というのは意識しておくとよいでしょう．

背理法が有効な証明問題の特徴｜具体例から２タイプを解説

「証明したいことを否定すると扱いやすくなる証明問題」では背理法が有効です．その具体例として「否定の証明」「『少なくとも〜』の証明」が挙げられます．

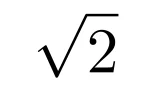
解答例

(1) まず直線$\mrm{EF}$と直線$\mrm{AC}$が平行であることを背理法により示す．

直線$\mrm{EF}$と直線$\mrm{AC}$が平行でなければ，これらはともに平面$\mrm{ABC}$上の直線だから交点をもつ．

Rendered by QuickLaTeX.com

よって，直線$\mrm{EF}$は平面$\mrm{OAC}$と交点をもつことになるから直線$\mrm{EF}$は平面$\mrm{OAC}$と平行でないが，これは$\Ve{DG}$と$\Ve{EF}$が平行であるという条件に矛盾するので，直線$\mrm{EF}$と直線$\mrm{AC}$は平行である．

平行線の同位角が等しいことから$\ang{BEF}=\ang{BAC}$かつ$\ang{BFE}=\ang{BCA}$が成り立つから，二角相等により$\tri{BAC}$と$\tri{BEF}$は相似なので，

$\begin{align*}\mrm{AE}:\mrm{EB}=\mrm{CF}:\mrm{FB}\end{align*}$

が従う．

(2) $\mrm{D},\mrm{E},\mrm{F},\mrm{G},\mrm{H},\mrm{I}$が正八面体の頂点であれば$\mrm{EF}=\mrm{FG}=\mrm{GD}=\mrm{DE}$である．よって，四角形$\mrm{EFGD}$は正方形なので，$\Ve{DG}$と$\Ve{EF}$は平行なので，(1)より

$\begin{align*}\mrm{AE}:\mrm{EB}=\mrm{CF}:\mrm{FB}\end{align*}$

が成り立つ．

Rendered by QuickLaTeX.com

同様に

$\begin{align*}\mrm{CF}:\mrm{FB}=\mrm{CI}:\mrm{IA},\quad \mrm{CI}:\mrm{IA}=\mrm{BE}:\mrm{EA}\end{align*}$

も成り立つから，$\mrm{AE}:\mrm{EB}=\mrm{BE}:\mrm{EA}$である．よって，$\mrm{AE}^2=\mrm{EB}^2$だから，$\mrm{AE}>0$かつ$\mrm{EB}>0$より$\mrm{AE}=\mrm{EB}$となって，

$\begin{align*}1:1=\mrm{AE}:\mrm{EB}=\mrm{CF}:\mrm{FB}=\mrm{CI}:\mrm{IA}\end{align*}$

を得る．よって，$2\mrm{IF}=\mrm{AB}$, $2\mrm{EF}=\mrm{AC}$だから，正八面体の仮定より成り立つ$\mrm{IF}=\mrm{EF}$と併せて$\mrm{AB}=\mrm{AC}$を得る．

四面体$\mrm{OABC}$の他の辺も同様に等しいことが分かるから，四面体$\mrm{OABC}$は正四面体である．

第３問

開く問題の表示/非表示

$p,q$を自然数，$\alpha,\beta$を

$\begin{align*}\tan{\alpha}=\dfrac{1}{p},\quad\tan{\beta}=\dfrac{1}{q}\end{align*}$

を満たす実数とする．このとき，

$\begin{align*}\tan(\alpha+2\beta)=2\end{align*}$

を満たす$p,q$の組$(p,q)$をすべて求めよ．

三角関数と整数の複合問題です．メインは整数と言いたいところですが，$\tan$の加法定理では気を付けたいことがあります．

解答への筋道

$\tan$の加法定理を用いると$\tan(\alpha+2\beta)$が$p,q$で表せることはすぐに気付きたいところで，ここから$p,q$の整数問題に持ち込みます．

$\tan$の加法定理

$\tan$の加法定理が

$\begin{align*}\tan(\theta+\phi)=\dfrac{\tan\theta+\tan\phi}{1-\tan\theta\tan\phi}\end{align*}$

であることは当たり前にしておきましょう．また，$\theta=\phi$とおくことで２倍角の公式

$\begin{align*}\tan2\theta=\dfrac{2\tan\theta}{1-\tan^2\theta}\end{align*}$

も得られますね．ただし，$\tan$の加法定理では$\tan\theta\tan\phi=1$の場合には分母が0になってしまい使えないことに注意してください．

本問では$\tan(\alpha+2\beta)$に加法定理，$\tan2\beta$に２倍角の公式を用いれば，$\tan{\alpha}$と$\tan{\beta}$の式になりますが，この変形をするためには

$\begin{align*}\tan{\alpha}\tan{2\beta}\neq1,\quad \tan{\beta}\neq1\end{align*}$

を示しておかなければならないわけですね．

因数分解と素因数分解

例えば，$0=3p+4q+2pq$のような不定方程式の整数解の候補は，方程式を$6=(p+2)(2q+3)$と変形することで

$\begin{align*}(p+2,2q+3)=(\pm1,\pm6),(\pm2,\pm3),(\pm3,\pm2),(\pm6,\pm1)\end{align*}$

と得られますね（複号同順）．このように，不定方程式の整数解を考えるとき因数分解と素因数分解を用いる方法は定石なので知っておきましょう．

さて，本問では$\tan(\alpha+2\beta)=2$を$p,q$で置き換えた等式は

$\begin{align*}q^2+4q-1=2p(q^2-q-1)\end{align*}$

となり，右辺の$q^2-q-1$と左辺の$q^2+4q-1$は２次の項と定数項が同じですから，

$\begin{align*}5q=(2p-1)(q^2-q-1)\end{align*}$

と変形できますね．

候補を減らす

因数分解と素因数分解を用いて不定方程式の整数解を考える方法では，全てのパターンを考えるのは非常に大変なことも少なくありません．

先ほどの挙げた例$0=3p+4q+2pq$の整数解の候補は複号同順で

$\begin{align*}(p+2,2q+3)=(\pm1,\pm6),(\pm2,\pm3),(\pm3,\pm2),(\pm6,\pm1)\end{align*}$

でしたが，$2q+3$は奇数ですから$\pm6$や$\pm2$にはなり得ません．そのため，整数解の候補は

$\begin{align*}(p+2,2q+3)=(\pm2,\pm3),(\pm6,\pm1)\end{align*}$

を減らすことができますね．あとはそれぞれで$p,q$を計算して整数解

$\begin{align*}(p,q)=(0,0),(-4,-3),(4,-1),(-8,-2)\end{align*}$

が得られます．

このように，あり得ないパターンを候補から消去することは，よくある方法なので知っておいてください．

本問で得られる方程式$5q=(2p-1)(q^2-q-1)$では，左辺の$q$と右辺の$q^2-q-1$は互いに素なので，$q$は$2p-1$を割り切るしかありません．

このことから$2p-1=\pm q,\pm5q$に絞られ，ここから整数解を求めることができますね．

解答例

[ステップ１] $\tan(\alpha+2\beta)=2$を$p,q$の等式に書き直す．

まず$\tan{\beta}=1$と仮定すると，$\beta=\dfrac{\pi}{4}+n\pi$（$n$は整数）と表せるから，

$\begin{align*}2&=\tan(\alpha+2\beta) =\tan\bra{\alpha+\dfrac{\pi}{2}+2n\pi} \\&=\tan\bra{\alpha+\dfrac{\pi}{2}} =-\frac{1}{\tan\alpha}=-p<0\end{align*}$

となり矛盾する．したがって，仮定は誤りで$\tan{\beta}\neq1$である．よって，$\tan{2\beta}$に２倍角の公式が使えて

$\begin{align*}\tan{2\beta} =\frac{2\tan\beta}{1-\tan^2\beta} =\frac{\frac{2}{q}}{1-\frac{1}{q^2}} =\frac{2q}{q^2-1}\end{align*}$

となる．ここで，$q=2$のときは$\tan{2\beta}=\dfrac{4}{3}$であり，$q\geqq3$のときは

$\begin{align*}q^2-2q-1=(q-1)^2-2>2^2-2=2>0\end{align*}$

より$\tan{\beta}=\dfrac{2q}{q^2-1}<1$である．よって，

$\begin{align*}\tan{\alpha}\tan{2\beta}=\frac{1}{p}\tan{2\beta}\neq1\end{align*}$

を得る．これより$\tan(\alpha+2\beta)$に加法定理が使えて

$\begin{align*}\tan(\alpha+2\beta)&=\frac{\tan\alpha+\tan2\beta}{1-\tan\alpha\tan2\beta} \\&=\frac{\frac{1}{p}+\frac{2q}{q^2-1}}{1-\frac{2q}{p(q^2-1)}} =\frac{q^2-1+2pq}{pq^2-p-2q}\end{align*}$

となる．$\tan(\alpha+2\beta)=2$より，

$\begin{align*}\frac{q^2-1+2pq}{pq^2-p-2q}=2 &\iff q^2-1+2pq=2pq^2-2p-4q \\&\iff q^2+4q-1=2p(q^2-q-1) \\&\iff 5q=(2p-1)(q^2-q-1)\quad\dots(*)\end{align*}$

となる．

[ステップ２] $(*)$の整数解$(p,q)$を求める．

$q$と$q^2-q-1$の共通素因数$r(\geqq2)$が存在すると仮定すると，$r$は$q$を割り切るので$q^2-q$を割り切るが$-1$は割り切らない．

これは$q^2-q-1$が素因数$r$をもつことに矛盾するから，仮定は誤りで$q$と$q^2-q-1$は互いに素である．

よって，$(*)$と併せて

$\begin{align*}(2p-1,q^2-q-1)=(\pm q,\pm5),(\pm 5q,\pm1)\end{align*}$

であり，

$\begin{align*}q^2-q-1=\bra{q-\frac{1}{2}}^2-\frac{3}{4}\geqq-\frac{3}{4}\end{align*}$

だから，$q^2-q-1=1,5$である．

$q^2-q-1=5$のとき
$\begin{align*}q^2-q-6=0\iff(q-3)(q+2)=0\end{align*}$

だから，$q\geqq2$より$q=3$である．このとき，$2p-1=q\iff p=2$を得る．
$q^2-q-1=1$のとき
$\begin{align*}q^2-q-2=0\iff(q-2)(q+1)=0\end{align*}$

となって，$q\geqq2$より$q=2$である．このとき，$2p-1=5q$となり$p$が自然数でないから不適である．

以上より，求める組は$(p,q)=(2,3)$である．

解答への筋道（別解）

不定方程式の整数解を求めるには，とりうる値の範囲を絞る方法も定石です．

不定方程式$q^2+4q-1=2p(q^2-q-1)$を$p$について解くと

$\begin{align*}p=\frac{q^2+4q-1}{2(q^2-q-1)}\end{align*}$

であり，右辺で多項式の割り算を実行して整理すると

$\begin{align*}p=\frac{1}{2}+\frac{5q}{2(q^2-q-1)} \iff 2p-1=\frac{5q}{q^2-q-1}\end{align*}$

となります．$2p-1$は整数なので$\dfrac{5q}{q^2-q-1}$も整数でなければなりません．

しかし，$\dfrac{5q}{q^2-q-1}$は$q$が大きければ$1$未満となって整数ではなくなるので，ここから$q$の候補が絞られます．

解答（別解）

$q^2+4q-1=2p(q^2-q-1)$を導出するまでは上の解答例と同じです．

$q^2+4q-1=2p(q^2-q-1)$を整理すると

$\begin{align*}2p-1=\frac{5q}{q^2-q-1}\end{align*}$

となる．$p$は自然数だから$2p-1\geqq2\cdot1-1=1$なので，

$\begin{align*}\frac{5q}{q^2-q-1}\geqq1 &\iff 5q\geqq q^2-q-1 \\&\iff 0\geqq q^2-6q-1 \\&\iff 3-\sqrt{10}\leqq q\leqq3+\sqrt{10}\end{align*}$

である．$3<\sqrt{10}<4$より$q=0,1,2,3,4,5,6$に限られるから，それぞれの場合で$q^2+4q-1=2p(q^2-q-1)$から$p$を考えればよい．

$q=0$のときは$-1=2p\cdot(-1)$となり$p$が自然数でないから不適．
$q=1$のときは$4=2p\cdot(-1)$となり$p$が自然数でないから不適．
$q=2$のときは$11=2p\cdot1$となり$p$が自然数でないから不適．
$q=3$のときは$20=2p\cdot5\iff p=2$を得る．
$q=4$のときは$31=2p\cdot11$となり$p$が自然数でないから不適．
$q=5$のときは$44=2p\cdot19$となり$p$が自然数でないから不適．
$q=6$のときは$59=2p\cdot29$となり$p$が自然数でないから不適．

以上より，求める組は$(p,q)=(2,3)$である．

第４問

開く問題の表示/非表示

$\tri{ABC}$は鋭角三角形であり，$\ang{A}=\dfrac{\pi}{3}$であるとする．また，$\tri{ABC}$の外接円の半径は$1$であるとする．

$\tri{ABC}$の内心を$\mrm{P}$とするとき，$\ang{BPC}$を求めよ．
$\tri{ABC}$の内接円の半径$r$の取りうる値の範囲を求めよ．

メインの考察は平面図形ですが，$r$が三角関数で表されるので公式をきちんと扱えるかが試されています．

解答への筋道

(1)は三角形の内角の和が$180^\circ$であることから瞬殺したい問題です．(2)は答えが予想できますが，それをきちんと三角関数の計算で示せるかがポイントです．

問題の捉え方

外接円の中心を$\mrm{O}$とすると，図は以下のようになっています．

各頂点の内角の２等分線の交点が内心なので，$\ang{PBA}=\ang{PBC}$と$\ang{PCA}=\ang{PCB}$が成り立っています．

条件から$\ang{A}$は$\dfrac{\pi}{3}$で一定なので，点$\mrm{B}$, $\mrm{C}$を固定すると円周角の定理の逆より外接円の半径は一定ですね．

このときの$\ang{BPC}$を求めるのが(1)ですね．

また，点$\mrm{A}$を動かすと内接円の半径$r$が変化するので，この$r$の動く範囲を求めるのが(2)ですね．

直感的には$\mrm{A}$が$\mrm{B}$や$\mrm{C}$に近付くと三角形が「潰れ」ていくので，$\tri{ABC}$が直角三角形に近付くほど$r$が小さくなり，$\ang{B}=\ang{C}$のとき$r$が最大となりそうですね．

外接円の半径と正弦定理

「外接円の半径」というワードがあれば，正弦定理をすぐに思い付きたいところです．

$\tri{ABC}$の外接円の半径が$1$であることから，$\tri{ABC}$に正弦定理を用いると

$\begin{align*}&\mrm{BC}=2\cdot1\cdot\sin{\ang{BAC}}=\sqrt{3}\end{align*}$

が成り立ちますね．

また「向かい合う辺の大きさと内角の大きさ」が絡むときにも正弦定理が有効なことも思い出しておきましょう．

いま線分$\mrm{BC}$の大きさが分かり，(1)より$\ang{BPC}$の大きさが得られています（$\ang{BPC}=120^\circ$となります）から，$\tri{PBC}$に正弦定理を用いると

$\begin{align*}&\frac{\mrm{PB}}{\sin\ang{PCB}}=\frac{\mrm{BC}}{\sin\ang{BPC}} \\\iff& \mrm{PB}=2\sin{\ang{PCB}}\end{align*}$

が成り立ちますね．

内接円の半径

点$\mrm{P}$から辺$\mrm{BC}$に下ろした垂線の足を$\mrm{H}$とすると，線分$\mrm{PH}$は$\tri{ABC}$の内接円の半径$r$ですね．

よって，$\tri{PBH}$に注目すると，正弦定理から得られた$\mrm{PB}=2\sin{\ang{PCB}}$と併せて

$\begin{align*}r=\mrm{PB}\sin{\ang{PBC}} =2\sin{\ang{PCB}}\sin{\ang{PBC}}\end{align*}$

が成り立ちます．ここで$\ang{PBC}=\theta$とおくと$\ang{PCB}$は$\theta$で表すことができ，結局$r$が$\theta$で表せますね．

ただし，問題の条件から$\tri{ABC}$が鋭角三角形であるような$\theta$しか動かないことに注意してください．

解答例

(1) 点$\mrm{P}$が$\tri{ABC}$の内心であることから，$\ang{PBA}=\ang{PBC}$と$\ang{PCA}=\ang{PCB}$が成り立つので，$\tri{ABC}$の内角の和を考えることにより

$\begin{align*}&\pi=\ang{ABC}+\ang{BCA}+\ang{CAB} \\\iff& \pi=2\ang{PBC}+2\ang{PCB}+\dfrac{\pi}{3} \\\iff& \dfrac{\pi}{3}=\ang{PBC}+\ang{PCB}\end{align*}$

が成り立つ．さらに$\tri{BPC}$の内角の和を考えることにより

$\begin{align*}\ang{BPC}=\pi-(\ang{PBC}+\ang{PCB})=\dfrac{2\pi}{3}\end{align*}$

を得る．

(2) $\ang{PBC}=\theta$とおく．$\tri{ABC}$が鋭角三角形であることと，

$\begin{align*}\begin{cases}0<\ang{ABC}<\frac{\pi}{2}\\0<\ang{BCA}<\frac{\pi}{2}\end{cases} \iff&\begin{cases}0<2\theta<\frac{\pi}{2}\\0<\frac{2\pi}{3}-2\theta<\frac{\pi}{2}\end{cases} \\\iff&\begin{cases}0<\theta<\frac{\pi}{4}\\\frac{\pi}{12}<\theta<\frac{\pi}{3}\end{cases} \\\iff&\frac{\pi}{12}<\theta<\frac{\pi}{4}\end{align*}$

は同値である．また，$\tri{ABC}$で正弦定理より，

$\begin{align*}\mrm{BC}=2\cdot1\cdot\sin\ang{BAC}=\sqrt{3}\end{align*}$

が成り立つ．よって，さらに$\tri{PBC}$で正弦定理より，

$\begin{align*}&\frac{\mrm{PB}}{\sin\ang{PCB}}=\frac{\mrm{BC}}{\sin\ang{BPC}} \\\iff& \frac{\mrm{PB}}{\sin\bra{\frac{\pi}{3}-\theta}}=\frac{\sqrt{3}}{\sin\frac{2\pi}{3}} \\\iff& \mrm{PB}=2\sin\bra{\frac{\pi}{3}-\theta}\end{align*}$

が成り立つ．よって，積和の公式と併せて

$\begin{align*}r&=\mrm{PB}\sin\theta =2\sin\bra{\frac{\pi}{3}-\theta}\sin\theta \\&=\cos\brb{\bra{\frac{\pi}{3}-\theta}-\theta}-\cos\brb{\bra{\frac{\pi}{3}-\theta}+\theta} \\&=\cos\bra{\frac{\pi}{3}-2\theta}-\cos\frac{\pi}{3} =\cos\bra{\frac{\pi}{3}-2\theta}-\frac{1}{2}\end{align*}$

$\dfrac{\pi}{12}<\theta<\dfrac{\pi}{4}$より$-\dfrac{\pi}{6}<\dfrac{\pi}{3}-2\theta<\dfrac{\pi}{6}$だから，

$\begin{align*}\frac{\sqrt{3}}{2}<\cos\bra{\frac{\pi}{3}-2\theta}\leqq1\end{align*}$

である．以上より，$r$の取りうる値の範囲は

$\begin{align*}\frac{\sqrt{3}-1}{2}<r\leqq\frac{1}{2}\end{align*}$

である．

第５問

開く問題の表示/非表示

$a\geqq0$とする．$0\leqq x\leqq\sqrt{2}$の範囲で，曲線$y=xe^{-x}$，直線$y=ax$，直線$x=\sqrt{2}$によって囲まれた部分の面積を$S(a)$とする．このとき，$S(a)$の最小値を求めよ．

（ここで，「囲まれた部分」とは，上の曲線または直線のうち２つ以上で囲まれた部分を意味するものとする．）

グラフで囲まれた面積を積分法で考える問題ですね．また，$S(a)$の式を処理する際に増減表を書きたいので，後半は微分法の問題となります．

解答への筋道

様子が分かれば積分計算は大して難しくないので確実に得点したい問題です．

$xy$平面上の曲線$y=xe^{-x}$と直線$x=\sqrt{2}$は以下のようになっています．

$a(\geqq0)$は直線$y=ax$の傾きを表すので，$a$が大き過ぎたり小さすぎたりすると下図のように囲まれる部分の面積$S(a)$は最小になりえないことが見てとれます．

よって，直線$y=ax$が曲線$y=xe^{-x}$と$0\leqq x\leqq\sqrt{2}$の範囲で交点を持つときに，面積$S(a)$が最小となりそうですね．

以上から$a$の値で場合分けすれば良さそうなことに気付きます．

解答例

曲線$y=xe^{-x}$，直線$y=ax$の共有点の$x$座標は

$\begin{align*}xe^{-x}=ax \iff x(e^{-x}-a)=0 \iff x=0,-\log{a}\end{align*}$

である．ただし，$a=0$のときは$x=0$のみである．よって，$0\leqq x\leqq\sqrt{2}$の範囲で共有点をもつための条件は

$\begin{align*}0\leqq-\log{a}\leqq\sqrt{2} \iff& 0\geqq\log{a}\geqq-\sqrt{2} \\\iff& 1\geqq a\geqq e^{-\sqrt{2}}\end{align*}$

である．

[1] $0\leqq a\leqq e^{-\sqrt{2}}$のとき

$\begin{align*}xe^{-x}-ax=x(e^{-x}-a)\geqq0\end{align*}$

だから，

$\begin{align*}S(a)=\int_{0}^{\sqrt{2}}xe^{-x}\,dx-a\int_{0}^{\sqrt{2}}x\,dx\end{align*}$

なので，$S(a)$は（$a$に関して）単調減少である．よって，$S\bra{e^{-\sqrt{2}}}\leqq S(a)$である．

[2]　$1\leqq a$のとき

$\begin{align*}xe^{-x}-ax=x(e^{-x}-a)\leqq0\end{align*}$

だから，

$\begin{align*}S(a)=a\int_{0}^{\sqrt{2}}x\,dx-\int_{0}^{\sqrt{2}}xe^{-x}\,dx\end{align*}$

なので，$S(a)$は（$a$に関して）単調増加である．よって，$S(1)\leqq S(a)$である．

[3] $e^{-\sqrt{2}}\leqq a\leqq 1$のとき

$0\leqq x\leqq-\log{a}$において$xe^{-x}-ax\geqq0$
$-\log{a}\leqq x\leqq \sqrt{2}$において$xe^{-x}-ax\leqq0$

だから，

$\begin{align*}S(a)=\int_{0}^{-\log{a}}(xe^{-x}-ax)\,dx+\int_{-\log{a}}^{\sqrt{2}}(ax-xe^{-x})\,dx\end{align*}$

である．

Rendered by QuickLaTeX.com

ここで，部分積分により

$\begin{align*}\int xe^{-x}\,dx &=\int x(-e^{-x})'\,dx =-xe^{-x}+\int e^{-x}\,dx \\&=-xe^{-x}-e^{-x}+C\end{align*}$

だから，

$\begin{align*}\int (xe^{-x}-ax)\,dx=-(x+1)e^{-x}-\frac{ax^{2}}{2}+C\end{align*}$

である（$C$は積分定数）．よって，

$\begin{align*}S(a)&=2\brb{-(-\log{a}+1)e^{-(-\log{a})}-\frac{a(-\log{a})^{2}}{2}} \\&\quad-\brb{-(0+1)e^{-0}-\frac{a\cdot0^{2}}{2}}-\brb{-(\sqrt{2}+1)e^{-\sqrt{2}}-\frac{a(\sqrt{2})^{2}}{2}} \\&=2\brb{a(\log{a}-1)-\frac{a(\log{a})^{2}}{2}}-(-1)-\brb{-(\sqrt{2}+1)e^{-\sqrt{2}}-a} \\&=2a\log{a}-a(\log{a})^{2}+(\sqrt{2}+1)e^{-\sqrt{2}}+1-a\end{align*}$

を得る．これより

$\begin{align*}S'(a) =&2\log{a}+2a\cdot\frac{1}{a}-(\log{a})^{2}-2a(\log{a})\cdot\frac{1}{a}-1 \\=&1-(\log{a})^{2} \\=&(1-\log{a})(1+\log{a})\end{align*}$

なので，$-\sqrt{2}\leqq\log{a}\leqq0$であることに注意すると

$\begin{align*}S'(a)=0 \iff\log{a}=-1 \iff a=e^{-1}\end{align*}$

である．よって，$e^{-\sqrt{2}}\leqq a\leqq 1$における$S(a)$の増減表は

$\begin{align*}\begin{array}{c||c|c|c|c|c} a & e^{-\sqrt{2}} & \dots & e^{-1} & \dots & \sqrt{2} \\ \hline S'(a) & - & - & 0 & + & + \\ \hline S(a) & S\bra{e^{-\sqrt{2}}} & \searrow & S\bra{e^{-1}} & \nearrow & S\bra{\sqrt{2}} \end{array}\end{align*}$

となるから，$S(a)$は$a=e^{-1}$のときに最小値$S(e^{-1})$をとる．

[1]-[3]より，$S(a)$は最小値

$\begin{align*}S(e^{-1}) &=2\brb{-(1+1)e^{-1}-\frac{e^{-1}\cdot1^{2}}{2}}-(-1)-\brb{-(\sqrt{2}+1)e^{-\sqrt{2}}-e^{-1}} \\&=1-4e^{-1}+(\sqrt{2}+1)e^{-\sqrt{2}}\end{align*}$

をとる．

第６問

開く問題の表示/非表示

$n$を自然数とする．$n$個の箱すべてに，$\fbox{1}$, $\fbox{2}$, $\fbox{3}$, $\fbox{4}$, $\fbox{5}$の５種類のカードがそれぞれ１枚ずつ計５枚入っている．各々の箱から１枚ずつカードを取り出し，取り出した順に左から並べて$n$桁の数$X$を作る．このとき，$X$が３で割り切れる確率を求めよ．

確率の問題ですが，$(n+1)$桁のときの確率が$n$桁のときの確率で表すことができるので，数列の漸化式に持ち込んで解くことができます．

解答への筋道

京都大学は確率漸化式の問題を好んで出題するので，準備していた人にとってはそう難しくないでしょう．

問題の捉え方

具体的に$n=5$のときに$X$が３で割り切れる確率を考えましょう．

整数が３で割り切れるためには，各位の数の和が３の倍数であることが必要十分条件であることは当たり前にしておきましょう．

例えば，最初の４枚で$\fbox{3}$, $\fbox{2}$, $\fbox{5}$, $\fbox{3}$と並んだ場合，ここまでの合計は１３なので，５桁の整数$X$が３で割り切れるためには残りの１枚は$\fbox{2}$または$\fbox{5}$となることが必要十分です．

他にも，最初の４枚で$\fbox{2}$, $\fbox{3}$, $\fbox{5}$, $\fbox{2}$と並んだ場合，ここまでの合計は１２なので，５桁の整数$X$が３で割り切れるためには残りの１枚は$\fbox{3}$となることが必要十分です．

このように，最初の４枚目までの合計がどのようになっているのかで，５枚目の候補が決まります．詳しくは，最初の４枚目までの合計の３で割った余りによって，５枚目の候補が決まります．

これを一般の$n$で考えると，$n-1$枚目までの合計を３で割った余りによって，$n$枚目の候補が決まりますね．

$a_{m+1}=ca_m+d$（$c\neq1$）型の漸化式

いまの考え方を用いると，$X$の$10^m$（$m=0,1,\dots,n-1$）の位までの各位の数の和を$p_m$としたとき，漸化式

$\begin{align*}p_{m+1}=-\frac{p_{m}}{5}+\frac{2}{5}\end{align*}$

が成り立ちます．

一般に１でない定数$c$と定数$d$に対して，漸化式$a_{m+1}=ca_m+d$は方程式$x=cx+d$を考えることで解くことができるのでした．

この方程式$x=cx+d$を漸化式$a_m=ca_m+d$の特性方程式と呼びますね．

$c\neq1$だから$x=cx+d$の解が存在します．この解を$\alpha$とすると$\alpha=c\alpha+d$が成り立つので，漸化式$a_{m+1}=ca_m+d$からこの等式で辺々引くと

$\begin{align*}a_{m+1}-\alpha=c(a_m-\alpha)\end{align*}$

となります．よって，数列$\{a_m-\alpha\}$が初項$a_1-\alpha$，公比$c$の等比数列であることが分かり，一般項が得られますね．

解答例

$X$が３で割り切れることと，$X$の各桁の数の和が３で割り切れることは同値である．

$X$の$10^{j}$の位の数を$a_{j}$とする．また，自然数$m$に対して$S_{m}=\sum_{j=1}^{m}a_{j}$とし，$S_{m}$を３で割った余りを$T_{m}$とする．さらに

$T_{m}=0$である確率を$p_{m}$
$T_{m}=1$である確率を$q_{m}$
$T_{m}=2$である確率を$r_{m}$

とすると，$T_{m}$は０，１，２のいずれかだから$p_{k}+q_{k}+r_{k}=1$が成り立つ．

求める確率は$p_{n}$である．すなわち，$T_n=0$となる確率を求めれば良い．

$T_{m+1}=0$であるためには

$T_{m}=0$かつ$a_{m+1}=3$
$T_{m}=1$かつ「$a_{m+1}=2$または$a_{m+1}=5$」
$T_{m}=2$かつ「$a_{m+1}=1$または$a_{m+1}=4$」

であることが必要十分だから，

$\begin{align*}p_{m+1}&=p_{m}\cdot\frac{1}{5}+q_{m}\cdot\frac{2}{5}+r_{m}\cdot\frac{2}{5} \\&=\frac{p_{m}}{5}+\frac{2}{5}(q_{m}+r_{m}) \\&=\frac{p_{m}}{5}+\frac{2}{5}(1-p_{m}) \\&=\frac{2}{5}-\frac{p_{m}}{5}\end{align*}$

が成り立つ．ここで得られた漸化式$p_{m+1}=\dfrac{2}{5}-\dfrac{p_{m}}{5}$は

$\begin{align*}&p_{m+1}=\frac{2}{5}-\frac{p_{m}}{5} \\\iff& p_{m+1}-\frac{1}{3}=-\frac{1}{5}(p_{m}-\frac{1}{3})\end{align*}$

と変形できるから，数列$\brb{p_{m}-\dfrac{1}{3}}$は初項$p_{1}-\dfrac{1}{3}$，公比$-\dfrac{1}{5}$の等比数列と分かる．

よって，$p_{1}=\dfrac{1}{5}$に注意して，

$\begin{align*}p_{n}-\frac{1}{3}&=\bra{-\frac{1}{5}}^{n-1}\bra{\frac{1}{5}-\frac{1}{3}} \\&=\frac{1}{3}+\frac{2}{3}\bra{-\frac{1}{5}}^{n}\end{align*}$