複素数の極形式は積・商に強く，とても簡単に計算できるのでした．
このことを応用すると，複素数$z$の累乗$z^n$（$n$は整数）も簡単に計算することができ，この極形式の累乗の計算について述べた定理をド・モアブルの定理といいます．
ド・モアブルの定理を用いれば，たとえば$(1-i)^5$のような計算も慣れれば数秒で求めることができます．
この記事では，
- 極形式を用いた計算の復習
- ド・モアブルの定理
- ド・モアブルの定理の証明
を順に説明します．
「複素数」の一連の記事
極形式を用いた計算の復習
極形式の積
［極形式の積］$r\geqq0$, $s\geqq0$とし，$\theta$, $\phi$を実数とする．複素数$z$, $w$を
\begin{align*}&z=r(\cos{\theta}+i\sin{\theta}),
\\&w=s(\cos{\phi}+i\sin{\phi})\end{align*}
と極形式で表したとき，
\begin{align*}zw=rs\{\cos{(\theta+\phi)}+i\sin{(\theta+\phi)}\}\end{align*}
が成り立つ．
つまり，
というわけですね．
極形式の商
［極形式の商］$r\geqq0$, $s\geqq0$とし，$\theta$, $\phi$を実数とする．複素数$z$, $w$を
\begin{align*}&z=r(\cos{\theta}+i\sin{\theta}),
\\&w=s(\cos{\phi}+i\sin{\phi})\end{align*}
と極形式で表したとき，
\begin{align*}\frac{z}{w}=\frac{r}{s}\{\cos{(\theta-\phi)}+i\sin{(\theta-\phi)}\}\end{align*}
が成り立つ．
つまり，
- 絶対値$r$の複素数を，絶対値$s$の複素数で割れば，絶対値$\dfrac{r}{s}$の複素数になる
- 偏角$\theta$の複素数を，偏角$\phi$の複素数で割れば，偏角$\theta-\phi$の複素数になる
というわけですね．とくに$z=1$とすると，$w$の逆数が
\begin{align*}w^{-1}=s^{-1}(\cos{(-\phi)}+i\sin{(-\phi)})\end{align*}
と表せることも分かりますね．
ド・モアブルの定理の考え方・内容と証明
ここで，ド・モアブルの定理の考え方と内容を説明し，その流れでド・モアブルの定理の証明をします．
ド・モアブルの定理の考え方
いま復習した複素数の極形式を用いた積と商をもとにして，複素数$z$の累乗$z^n$（$n$は整数）がどのように計算できるか考えましょう．
２つの複素数$z=r(\cos{\theta}+i\sin{\theta})$と$z=r(\cos{\theta}+i\sin{\theta})$の積は，上で復習した極形式の積なので
\begin{align*}z^2&=r\cdot r(\cos{(\theta+\theta)}+i\sin{(\theta+\theta)})
\\&=r^2(\cos{(2\theta)}+i\sin{(2\theta)})\end{align*}
が成り立つことが分かります．さらに，$z$と$z^2$の積を考えれば，
\begin{align*}z^3&=r^2\cdot r(\cos{(2\theta+\theta)}+i\sin{(2\theta+\theta)})
\\&=r^3(\cos{(3\theta)}+i\sin{(3\theta)})\end{align*}
が成り立つことが分かります．
これを続けていけば，任意の自然数$n$に対して，
\begin{align*}z^n=r^n(\cos{(n\theta)}+i\sin{(n\theta)})\end{align*}
が成り立ちそうですね．
また，$z^{-1}=r^{-1}(\cos{(-\theta)}+i\sin{(-\theta)})$なので，これを$n$回積をとると，同様に
\begin{align*}z^{-n}=r^{-n}\{\cos{(-n\theta)}+i\sin{(-n\theta)}\}\end{align*}
となりそうですね．
ド・モアブルの定理の内容
以上をまとめたものが，次のド・モアブルの定理です．
［ド・モアブルの定理］$r\geqq0$とし，$\theta$を実数とする．このとき，極形式で表された複素数
\begin{align*}z=r(\cos{\theta}+i\sin{\theta})\end{align*}
と任意の整数$n$に対して，
\begin{align*}z^n=r^n(\cos{(n\theta)}+i\sin{(n\theta)})\end{align*}
が成り立つ．
上の考え方で触れたように，ド・モアブルの定理は$n$が負の場合であっても成り立つことにも注意しておきましょう．
ド・モアブルの定理の証明
ド・モアブルの定理は$z$を「繰り返し」かけていくイメージでしたから，これをきちんと証明するには数学的帰納法を用いればいいですね．
［１］$n\ge0$の場合に成り立つことを数学的帰納法により示す．
(i) $n=0$のとき
\begin{align*}z^n&=z^0=1
\\&=r^0(\cos{(0\theta)}+i\sin{(0\theta)})\end{align*}
が成り立つ．
(ii) $n=k$ ($k\ge0$)のとき$z^n=r^n(\cos{(n\theta)}+i\sin{(n\theta)})$が成り立つとすると，極形式の積の公式より
\begin{align*}z^{k+1}=&zz^k
\\=&r(\cos{\theta}+i\sin{\theta})\cdot r^k(\cos{(k\theta)}+i\sin{(k\theta)})
\\=&rr^{k}\{\cos{(\theta+k\theta)}+i\sin{(\theta+k\theta)}\}
\\=&r^{k+1}\{\cos{(k+1)\theta}+i\sin{(k+1)\theta)}\}\end{align*}
が成り立つ．
(i), (ii)より任意の自然数$n$に対して$z^n=r^n(\cos{(n\theta)}+i\sin{(n\theta)})$が成り立つ．
［２］$n<0$の場合に成り立つことを［１］を利用して示す．
$n=-m$とすると$m>0$なので，［１］で示したことから
\begin{align*}z^n&=z^{-m}=(z^{-1})^{m}
\\&=\{r^{-1}(\cos{(-\theta)}+i\sin{(-\theta)})\}^{m}
\\&=r^{-m}\{\cos{(-m\theta)}+i\sin{(-m\theta)}\}
\\&=r^{n}\{\cos{(n\theta)}+i\sin{(n\theta)}\}\end{align*}
が成り立つ．
［２］の$n<0$の場合の証明も，負の方向へ進む数学的帰納法で示しても問題ありません．
ド・モアブルの定理の具体例
最後にド・モアブルの定理を用いて次の問題を解きましょう．
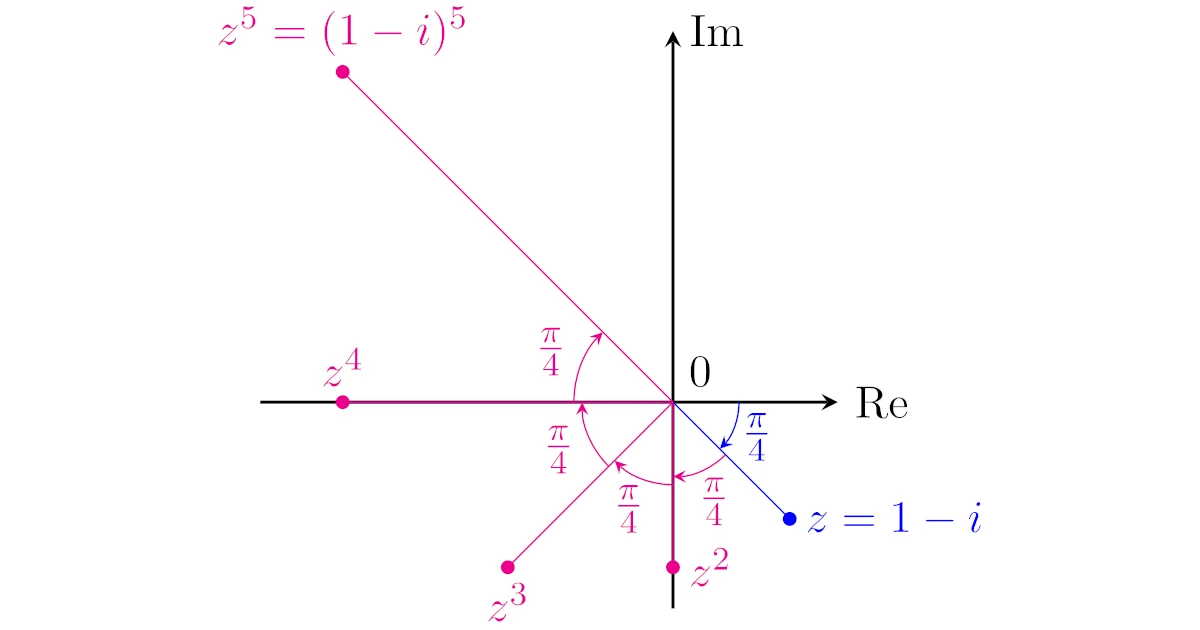
$(1-i)^5$を計算せよ．
複素数の指数計算なので，ド・モアブルの定理が第一感です．そのため$1-i$を極形式で表して，ド・モアブルの定理を用いましょう．
$1-i$の絶対値は
\begin{align*}|1-i|=\sqrt{1^2+(-1)^2}=\sqrt{2}\end{align*}
なので，$1-i$の極形式は
\begin{align*}1-i&=\sqrt{2}\bra{\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i}
\\&=\sqrt{2}\bra{\cos\bra{-\frac{\pi}{4}}+i\sin\bra{-\frac{\pi}{4}}}\end{align*}
となる．よって，ド・モアブルの定理より
\begin{align*}(1-i)^5&=\sqrt{2}^5\bra{\cos\bra{-\frac{5\pi}{4}}+i\sin\bra{-\frac{5\pi}{4}}}
\\&=4\sqrt{2}\bra{-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i}
\\&=4(-1+i)\end{align*}
である．
図形的には下図のようになっていますね．
コメント