複素平面上の点とベクトルの拡大縮小・回転は極形式で考える

複素数の積には極形式が便利で，２つの複素数$z$, $w$が

$z=r(\cos{\theta}+i\sin{\theta})$
$w=s(\cos{\phi}+i\sin{\phi})$

と表されていれば，積$zw$は

$\begin{align*}zw=rs(\cos{(\theta+\phi)}+i\sin{(\theta+\phi)})\end{align*}$

と絶対値の積，偏角の和により求まるのでした．

さて，この極形式の積の見方を少し変えれば，複素平面上の拡大縮小・回転を考えることができます．

この記事では，複素平面上の

点の拡大縮小・回転
ベクトルの拡大縮小・回転

を順に説明します．

「複素数」の一連の記事

点の拡大縮小・回転
1. ステップ１（原点中心の場合）
2. ステップ１（一般の点中心の場合）
ベクトルの拡大縮小・回転
1. 複素平面上のベクトル
2. ベクトルの拡大縮小・回転

点の拡大縮小・回転

複素平面上の点の拡大縮小・回転を

原点中心の場合
一般の点中心の場合

の２ステップで考えましょう．

ステップ１（原点中心の場合）

冒頭で書いたように極形式で表された２つの複素数$z=r(\cos{\theta}+i\sin{\theta})$, $w=s(\cos{\phi}+i\sin{\phi})$に対して，

$\begin{align*}zw=rs\{\cos{(\theta+\phi)}+i\sin{(\theta+\phi)}\}\end{align*}$

が成り立ちます．このとき，複素平面上で複素数$z$が表す点を$\mrm{P}$とし，複素数$zw$が表す点を$\mrm{Q}$とすると下図のようになりますね．

つまり，複素平面上の複素数$z$が表す点に対して

原点$\mrm{O}(0)$からの距離を$s$倍
原点$\mrm{O}(0)$中心に偏角を$+\phi$

した点が複素数$zw$の表す点となっています．

このことは，以下のように表すことができますね．

[原点中心の点の回転] $s\geqq0$, $\phi$を実数とする．複素平面上の点$\mrm{P}(z)$に対して，複素数

$\begin{align*}z'=z\cdot s(\cos{\phi}+i\sin{\phi})\end{align*}$

が表す点$\mrm{Q}(z’)$は原点中心に$s$倍拡大，$+\phi$回転した点である．

要するに，複素平面上の点$\mrm{P}(z)$に対して，

原点からの距離を$s$倍したければ，$z$に$s$をかければよく
原点中心に偏角を$+\phi$したければ，$z$に$\cos{\phi}+i\sin{\phi}$をかければよい

というわけですね．

ステップ１（一般の点中心の場合）

次に，複素平面上の原点とは限らない点$\mrm{A}(\alpha)$中心の拡大縮小・回転を考えましょう．

複素平面上の点$\mrm{P}(z)$に対して，

点$\mrm{A}(\alpha)$からの距離を$s$倍
点$\mrm{A}(\alpha)$中心に偏角を$+\phi$

した点を$\mrm{Q}(z’)$としましょう．

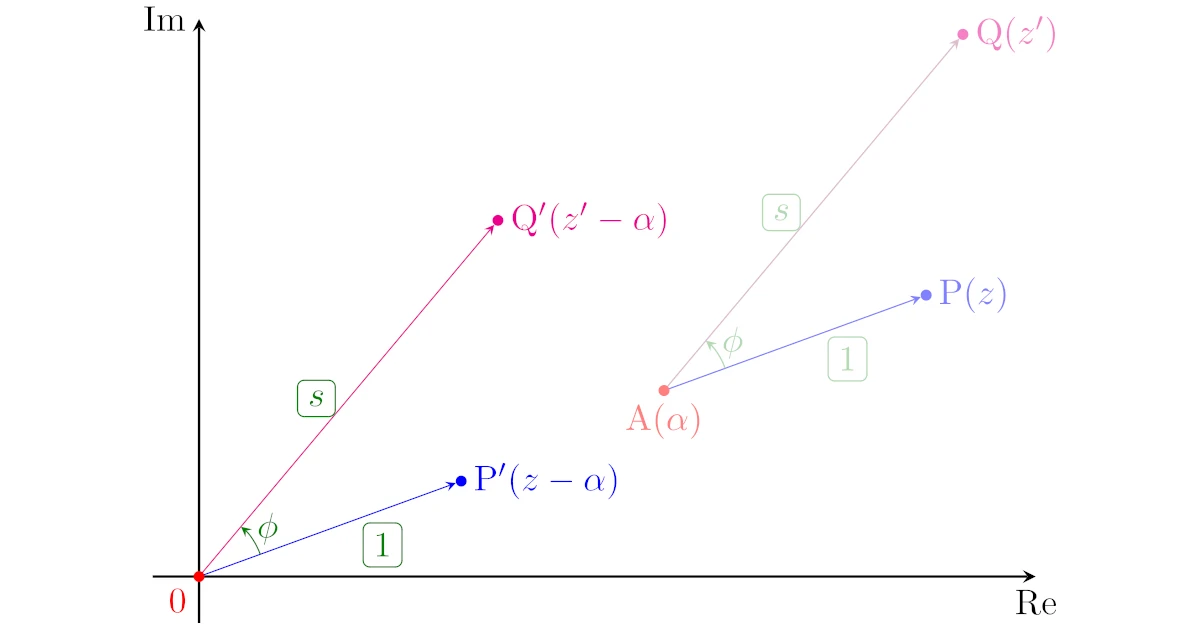
このとき，点$\mrm{A}$が原点$\mrm{O}(0)$にくるように全体を平行移動させると，点$\mrm{P}$は点$\mrm{P’}(z-\alpha)$，点$\mrm{Q}$は点$\mrm{Q’}(z’-\alpha)$に移ります．

点$\mrm{Q’}(w-\alpha)$は，点$\mrm{P’}(z-\alpha)$に対して

原点$\mrm{O}(0)$からの距離を$s$倍
原点$\mrm{O}(0)$中心に偏角を$+\phi$

した点となっているので，先ほどみた原点中心の拡大縮小・回転の考え方から

$\begin{align*}&z'-\alpha=(z-\alpha)\cot s(\cos{\phi}+i\sin{\phi}) \\\iff&z'=(z-\alpha)\cdot s(\cos{\phi}+i\sin{\phi})+\alpha\end{align*}$

が成り立ちます．以上をまとめると，以下のようになりますね．

$s\geqq0$, $\phi$を実数とする．複素平面上の点$\mrm{A}(\alpha)$，点$\mrm{P}(z)$に対して，複素数

$\begin{align*}z'=(z-\alpha)\cdot s(\cos{\phi}+i\sin{\phi})+\alpha\end{align*}$

が表す点$\mrm{Q}(z’)$は点$\mrm{A}$中心に$s$倍拡大，$+\phi$回転した点である．

当然のことながら，$\alpha=0$の場合には

$\begin{align*}z'=z\cdot s(\cos{\phi}+i\sin{\phi})\end{align*}$

となって，原点中心の拡大縮小・回転と一致しますね．

ベクトルの拡大縮小・回転

いまみた複素平面上の点$\mrm{A}(\alpha)$中心の拡大縮小・回転の式は

$\begin{align*}z'-\alpha=(z-\alpha)\cdot s(\cos{\phi}+i\sin{\phi})\end{align*}$

でしたが，これは複素平面上のベクトルの拡大縮小・回転と考えると，すっきり説明ができます．

複素平面上のベクトル

$xy$平面は複素平面と同一視できるので，$xy$平面上のベクトルは複素平面上のベクトルと同一視できます．例えば，

$xy$平面上の点$\mrm{A}(1,1)$, $\mrm{B}(4,3)$に対して，$\Ve{AB}=(3,2)$
複素平面上の点$\mrm{A}(1+i)$, $\mrm{B}(4+3i)$に対して，$\Ve{AB}=3+2i$

が対応するわけですね．

このように，複素平面上の２点$\mrm{A}(\alpha)$, $\mrm{B}(\beta)$があるとき，$\Ve{AB}$は複素数$\beta-\alpha$で表すことができます．

ベクトルの拡大縮小・回転

このように考えると，複素平面上の点$\mrm{P}(z)$の点$\mrm{A}(\alpha)$中心の拡大縮小・回転

$\begin{align*}z'-\alpha=(z-\alpha)\cdot s(\cos{\phi}+i\sin{\phi})\end{align*}$

は，$z-\alpha$で表されるベクトル$\Ve{AP}$を拡大縮小・回転して$z’-\alpha$で表されるベクトル$\Ve{AQ}$になっているということもできますね．

このように，

点$\mrm{A}(\alpha)$中心の回転
点$\mrm{A}(\alpha)$を始点とするベクトルの回転

は同じものとみることができます．以上をまとめると，次のようになりますね．

[ベクトルの回転] $s\geqq0$, $\phi$を実数とする．複素平面上の３点$\mrm{A}(\alpha)$, $\mrm{P}(z)$, $\mrm{Q}(z’)$に対して，

$\begin{align*}z'-\alpha=(z-\alpha)\cdot s(\cos{\phi}+i\sin{\phi})\end{align*}$

が成り立つとき，ベクトル$\Ve{AQ}$はベクトル$\Ve{AP}$を$s$倍拡大，$+\phi$回転してできるベクトルである．

複素数８
複素平面上の拡大縮小・回転は極形式で考える

点の拡大縮小・回転

ステップ１（原点中心の場合）

ステップ１（一般の点中心の場合）

ベクトルの拡大縮小・回転

複素平面上のベクトル

ベクトルの拡大縮小・回転

コメント