前回の記事で説明したように,関数$f$の点$a$での微分係数$f'(a)$は
と定義され,$y=f(x)$の$x=a$の接線の傾きを表すのでした.
しかし,毎回この定義式に従って微分係数$f'(a)$を求めるのは少々面倒です.
そこで,微分係数より扱いやすい導関数というものがあります.
この記事では,
- 微分係数の復習
- 導関数の定義
- 導関数の具体例
を順に説明します.
「微分法」の一連の記事
微分係数から導関数へ
導関数の考え方を理解するために,まずは前回の記事で扱った微分係数を少し観察するところから始めましょう.
微分係数の復習
微分係数は以下のように定義されるのでした.
関数$f(x)$と実数$a$に対して,
が存在すれば,この値を関数$f(x)$の$x=a$における微分係数といい,$f'(a)$と表す.
$\lim\limits_{h\to 0}\dfrac{f(a+h)-f(a)}{h}$で$h=b-a$とおくと$\lim\limits_{b\to a}\dfrac{f(b)-f(a)}{b-a}$になるので,これらはどちらも同じものなのでした.
これについて詳しくは以下の記事を参照してください.
$f(x)=x^2$に対して,2つの微分係数$f'(1)$, $f'(-2)$を求めよ.
微分係数の定義より,
より$f'(1)=2$であり,
より$f'(-2)=-4$である.
この解答例から$f'(1)$も$f'(2)$も分母と分子を約分することがポイントであり,本質的にはどちらも同じ計算をしているということに気付きますね.
そこで「わざわざ導関数$f'(a)$の$a$を指定しなくても,変数$x$のまま$f'(x)$も同様に求められるのではないか」という考えができます.
導関数の定義
このように考えてできたものが導関数です.
関数$f(x)$に対して,定義域上の任意の実数$a$に対して,$x=a$で導関数が存在するとする.このとき,
で定まる関数$f'(x)$を$f(x)$の導関数といい,導関数を求めることを微分するという.
また,関数$y=f(x)$に対して,$f'(x)$は
などとも表す.
具体的に$f(x)=x^2$の導関数を求めると,
となります.これより,
- $x=1$を代入して$f'(1)=2$
- $x=-2$を代入して$f'(-2)=-4$
なので,先ほどの微分係数の定義から別々に求めたものと(当然ながら)同じ答えが得られていますね!
このように$x$を固定せずに$x$のまま考えてできる関数を導関数というわけですね.
導関数の具体例
最後にもう少し具体例を考えてみましょう.
例1
関数$f(x)=x$を微分せよ.
導関数の定義より
となって,$f'(x)=1$を得る.
つまり,どの$x$でも($x=0$でも$x=1$でも$x=-\pi$でも)接線の傾きが$1$という結果になったわけですが,$y=x$のグラフは$x$軸に対して$45^\circ$をなす直線ですから,どこででも傾きが$1$で一定なのは当然ですね.
例2
関数$f(x)=1$を微分せよ.
導関数の定義より
となって,$f'(x)=0$を得る.
つまり,どの$x$でも($x=0$でも$x=1$でも$x=-\pi$でも)接線の傾きが$0$という結果になったわけですが,$y=1$のグラフは$x$軸に平行な直線ですから,どこででも傾きが$0$で一定なのは当然ですね.
例3
関数$f(x)=2x^{3}$を微分せよ.
導関数の定義より
となって,$f'(x)=6x^2$を得る.
この結果より,例えば$x=0,-1,-10\pi$とすると
- $f'(0)=0$
- $f'(-1)=6\times(-1)^2=6$
- $f'(-10\pi)=6\times(-10\pi)^2=600\pi^2$
となりますね.
このように導関数$f'(x)$が分かっていれば,$x$に具体的に代入することで微分係数は瞬時に求まりますね.
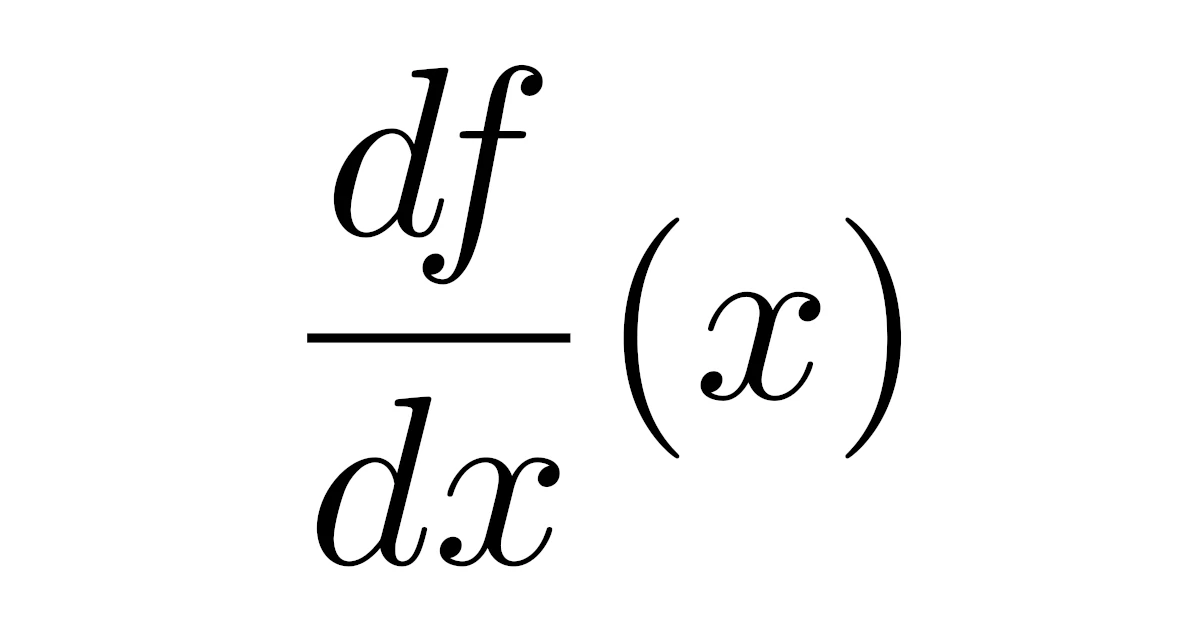
コメント